Large top heap: Based on the complete binary tree, the value of each node is greater than or equal to the value of its left and right child nodes

p moves forward through the loop p -- pointer in the main function

 public static void main(String[] args) {
        int[] arr = {8,7,3,5,4,9,1,3};
        for (int p = arr.length-1;p>=0;p--){
            adjustHeap(arr,p,arr.length);
        }
    }

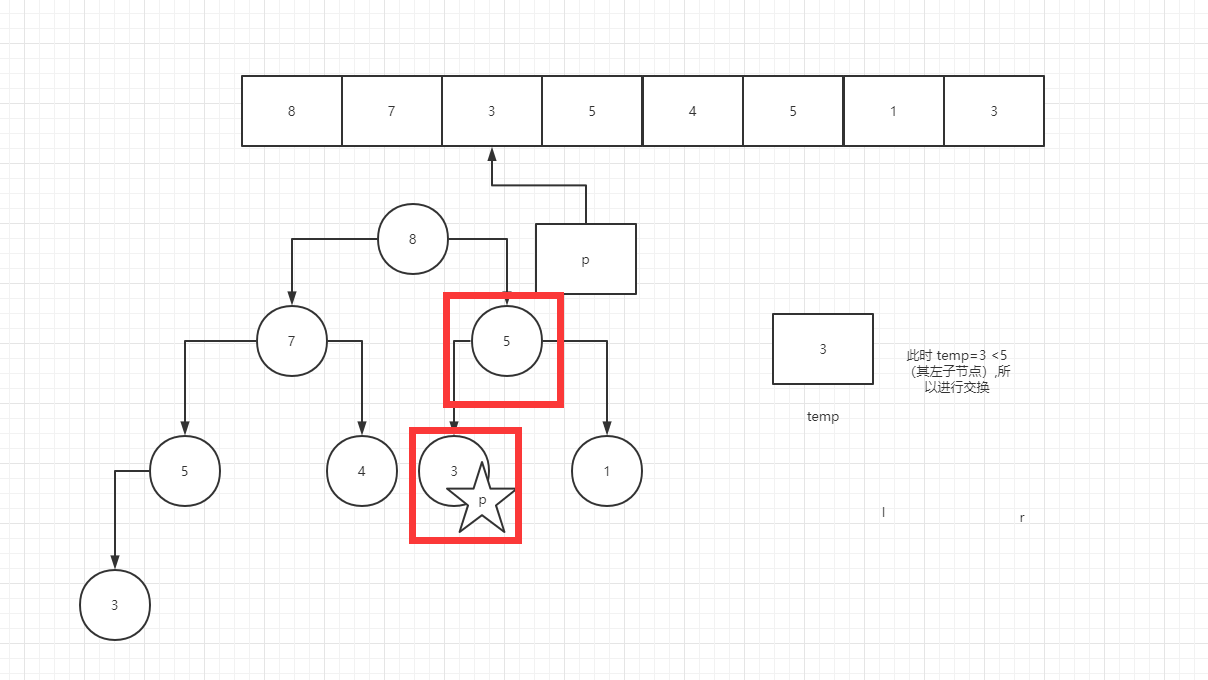
In the fifth cycle, we finally found the son node

But at this time, temp = 5 > 3 does not meet the exchange conditions, so continue to move forward

 

At this time, temp = 3 < 5 (its left child node), so exchange

Now it becomes

public static void adjustHeap(int[] arr,int parent,int length){
          // Define the value of the parent node
        int temp = arr[parent];
        //Define left child
        int lChild = 2 * parent +1;
		//The purpose of the loop is to check whether the child node after the exchange has a child node. If so, compare the size again
        while (lChild <length){
            // Define right child
            int rChild = lChild + 1;
            // Find out who is the biggest of the left and right children
            if (rChild <length && arr[lChild] <arr[rChild]){
                lChild++;
            }

            if (temp >= arr[lChild]){
                break;
            }

            // Assign the value of the child node to the position of the parent node
            arr[parent] = arr[lChild];

            parent = lChild;
            lChild = 2 * lChild+1;
        }
        arr[parent] = temp;
    }

The while loop is to check whether the child node after the exchange has a child node. If so, compare the size again

 while (lChild <length){
            // Define right child
            int rChild = lChild + 1;
            // Find out who is the biggest of the left and right children
            if (rChild <length && arr[lChild] <arr[rChild]){
                lChild++;
            }

            if (temp >= arr[lChild]){
                break;
            }

            // Assign the value of the child node to the position of the parent node
            arr[parent] = arr[lChild];

            parent = lChild;
            lChild = 2 * lChild+1;
        }

At this time, the pointer of the parent refers to its child node, and the pointer of its child node refers to the child node of the transformed child node

At this time, there are no child nodes on the transformed parent

So not satisfied

  while (lChild <length)

So end the while loop

implement

 arr[parent] = temp;

The completion of this step marks the completion of the exchange

End this for loop

 

Continue the for loop

 

 

The value of the parent node is still larger than that of the child node. Do not exchange and continue to move forward

 

At this time, a large top pile is generated, and the maximum value is generated

To sort the heap, you need to generate a large top heap with an array length

public class HeapSort {
    public static void main(String[] args) {
        int[] arr = {8,7,3,5,4,9,1,3};
        int l=arr.length;
        int[] sort =new int[arr.length];
        for(int i=sort.length-1;i>=0;i--) {
          for (int p = l-1;p>=0;p--){
            adjustHeap(arr,p,l);  
          }
        sort[i]=arr[0];
        arr[0]=arr[l-1];
        l--;
       }
        System.out.println(Arrays.toString(sort));
    }

A layer of for loop is set outside the for loop that originally generated the large top heap

After the completion of the internal for loop, a large top heap is generated, that is, a current maximum value, which is placed at the last bit of the new array

 sort[i]=arr[0];

And remove the first bit of the arr array and put the last bit in the first place, which means that the length of the array is reduced by one

  arr[0]=arr[l-1];
        l--;

Through two-layer loop, we get an array sorted from large to small

This is heap sorting

Source code:

import java.util.Arrays;

public class HeapSort {
    public static void main(String[] args) {
        int[] arr = {8,7,3,5,4,9,1,3};
        int l=arr.length;
        int[] sort =new int[arr.length];
        for(int i=sort.length-1;i>=0;i--) {
          for (int p = l-1;p>=0;p--){
            adjustHeap(arr,p,l);  
          }
        sort[i]=arr[0];
        arr[0]=arr[l-1];
        l--;
       }
        System.out.println(Arrays.toString(sort));
    }

    public static void adjustHeap(int[] arr,int parent,int length){
          // Define the value of the parent node
        int temp = arr[parent];
        //Define left child
        int lChild = 2 * parent +1;
		//The purpose of the loop is to check whether the child node after the exchange has a child node. If so, compare the size again
        while (lChild <length){
            // Define right child
            int rChild = lChild + 1;
            // Find out who is the biggest of the left and right children
            if (rChild <length && arr[lChild] <arr[rChild]){
                lChild++;
            }

            if (temp >= arr[lChild]){
                break;
            }

            // Assign the value of the child node to the position of the parent node
            arr[parent] = arr[lChild];

            parent = lChild;
            lChild = 2 * lChild+1;
        }
        arr[parent] = temp;
    }
}