Some codes involve the knowledge mentioned before
Quick sort
Two way fast platoon
Improve according to the one-way fast sorting in the previous section. In order to prevent each cycle, the same number is on one side, such as:
3 4 1 2 3 2 1 3 1 3 5 4
Single way fast platoon: 1 1 2 1 3 3 3 4 5 4
In this way, the case equal to three is all on the left. We want to divide the case equal to three equally on both sides, that is, two-way fast platoon
Mainly use two pointers for traversal, mainly to understand the code
Two way fast sorting code
package p5.Sorting algorithm;
//Two way quick sort
public class QuickSort02 extends Sort {
public QuickSort02(int[] arr) {
super(arr);
}
@Override
public void sort() {
quickSort(0, arr.length - 1);
}
private void quickSort(int L, int R) {
if (L >= R) {
return;
}
//Divide the array and return the midpoint after division
int p = partition(L, R);
quickSort(L,p - 1);
quickSort(p + 1, R);
}
private int partition(int L, int R) {
//Optimize the random number and change the following number with the first number
//Try to avoid extreme cases (ascending cases)
swap(L, (int) (Math.random() * (R - L + 1) + L));
int v = arr[L];
int i = L + 1;
int j = R;
while (true) {
while (i <= R && arr[i] < v) {
i++;
}
while (j >= L + 1 && arr[j] > v) {
j--;
}
if (i > j) {
break;
}
swap(i,j);
i++;
j--;
}
swap(L,j);
return j;
}
}
Three way fast platoon
Continue to improve the two-way fast platoon. As we said above, for equal cases, we divide it equally on both sides for the next sorting
Now 3 think 3, now 3 is 1, 2
Is it necessary to do the next sorting?
Three way sorting is to solve this problem,
We need three pointers here
Understanding code
Three way fast sorting code
package p5.Sorting algorithm;
import java.util.Arrays;
public class QuickSort03 extends Sort {
public QuickSort03(int[] arr) {
super(arr);
}
@Override
public void sort() {
quickSort(0, arr.length - 1);
}
private void quickSort(int L, int R) {
if (L >= R) {
return;
}
swap(L, (int) (Math.random() * (R - L + 1) + L));
int v = arr[L];
int lt = L;
int gt = R + 1;
int i = L + 1;
while (i < gt) {
if (arr[i] < v) {
swap(i, lt + 1);
lt++;
i++;
} else if (arr[i] > v) {
swap(i,gt - 1);
gt--;
} else {
i++;
}
}
swap(L,lt);
quickSort(L,lt - 1);
quickSort(gt, R);
}
}
The above sort is comparison sort (judged by greater than or less than sign). Another comparison sort is heap sort, which will be summarized later. Next, we summarize several non comparison sort, collectively referred to as bucket sort.
Bucket sorting mainly classifies numbers to achieve the purpose of sorting
Cardinality sort
Cardinality sorting is to sort first according to the low order, and then collect; Then sort according to the high order, and then collect; And so on until the highest position. Sometimes some attributes have priority order. They are sorted by low priority first, and then by high priority. The final order is high priority, high priority first, high priority with the same low priority, high priority first.
Time complexity: O(n+m)
Space complexity: O(n+m)
Stability: stable
thinking
Data: 345 12 67 8 32 12 21 16 120 232
Step 1: classify by single digit to get
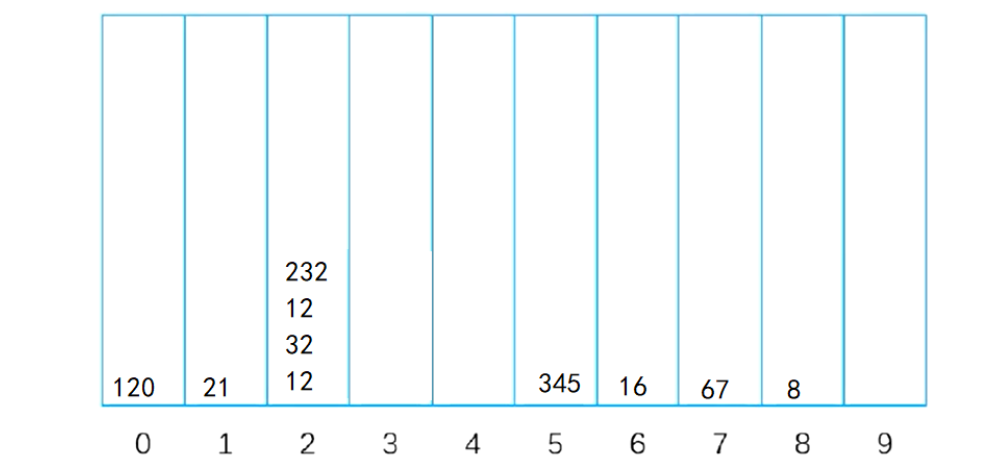Then take out the data in turn to get: 120 21 12 32 12 232 345 16 67 8 > > Step 2: classify according to ten digits, and then press it into the bucket in turn to get >
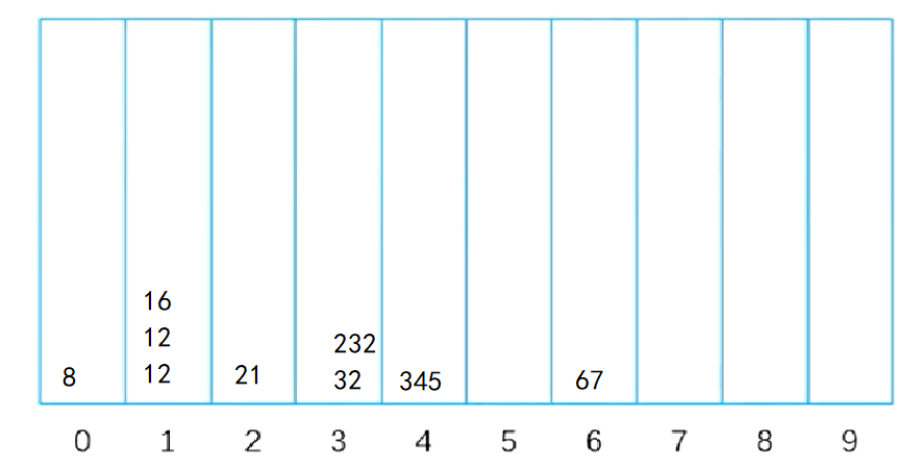
Take out the data in turn and get: 8 12 12 16 21 32 232 345 67
Step 3: classify by hundreds and press it into the barrel again
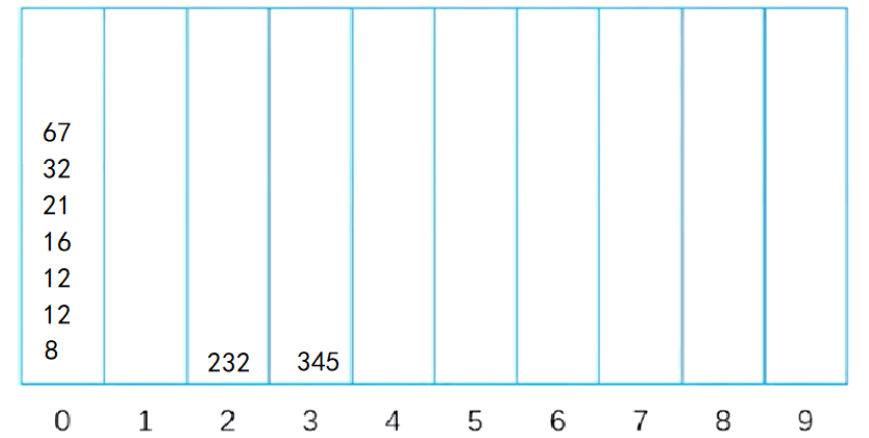
Then take out the data in turn: 8 12 12 16 21 32 67 232 345
end
Therefore, the number of cycles depends on the maximum number. You need to find the maximum number in advance and then carry out this cycle
This also has disadvantages. If all numbers are very small and a very large number suddenly comes, the time complexity will increase. Therefore, the numbers are quite different and are not recommended
Cardinality sorting code
package p5.Sorting algorithm;
import p3.Chain structure.LinkedList;
//Cardinality sort
public class RadixSort extends Sort{
public RadixSort(int[] arr) {
super(arr);
}
@Override
public void sort() {
//1. Find classification - number of rounds collected (maximum length)
int radix = getRadix();
//2. Create a bucket list and a collection of all buckets. Each bucket is used as a queue by LinkedList
LinkedList<Integer>[] list = new LinkedList[10];
for (int i = 0; i < list.length; i++) {
list[i] = new LinkedList<>();
}
//3. Start classification - Collection
for (int r = 1; r <= radix; r++) {
//Classification process
for (int i = 0; i < arr.length; i++) {
list[getIndex(arr[i], r)].offer(arr[i]);
}
int index = 0; //Traversing the original array of arr
//Collection process
for (int i = 0; i < list.length; i++) {
while (!list[i].isEmpty()) {
arr[index++] = list[i].poll();
}
}
}
}
private int getIndex(int num, int r) {
int ret = 0;
for (int i = 1; i <= r; i++) {
ret = num % 10;
num /= 10;
}
return ret;
}
private int getRadix() {
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
return (max + "").length();
}
}
Bucket sorting
Bucket sorting is an upgraded version of counting sorting. It makes use of the mapping relationship of the function. The key to efficiency lies in the determination of the mapping function. Working principle of bucket sort: assuming that the input data is uniformly distributed, divide the data into a limited number of buckets, and then sort each bucket separately (it is possible to use another sorting algorithm or continue to use bucket sorting recursively).
Time complexity: O(n+m)
Space complexity: O(n+m)
Stability: stable
thinking
Data: 12 31 21 33 9 7 24 12 3 21 33 11
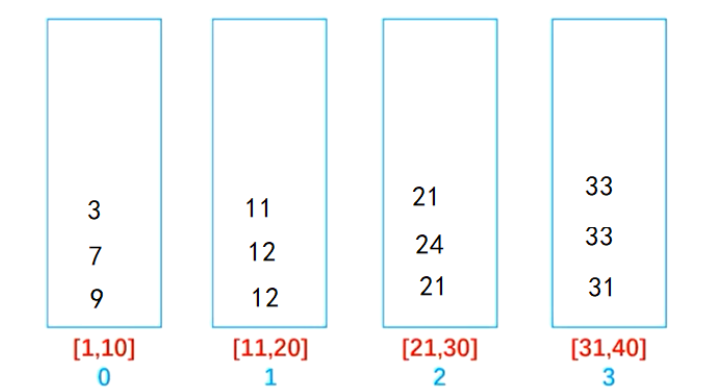
To get such data, there is sorting between each bucket. Next, we only need to sort the data in the bucket. As for the sorting method of data in the bucket, we can use any method or always sort in the bucket
Here, we need to pay attention to how to determine the number of buckets and the data range in the bucket
As long as the number of barrels is determined, the range is determined (average score)
Bucket range: ((max) - (min)) / (array length) + 1
For example, if the maximum value is 40, the minimum value is 1 and the length is 10, then the number of barrels is (40-1) / 10 + 1. If you do not add 1, you will get 3 barrels and miss the data
Bucket sort code
package p5.Sorting algorithm;
import p2.linear structure.ArrayList;
import java.util.Comparator;
public class BucketSort extends Sort{
public BucketSort(int[] arr) {
super(arr);
}
@Override
public void sort() {
//1. Find the maximum and minimum values
int max = arr[0];
int min = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
if (arr[i] < min) {
min = arr[i];
}
}
//2. Determine the number of buckets and create buckets
int bucketNum = (max - min) / arr.length + 1;
ArrayList<Integer> list[] = new ArrayList[bucketNum];
for (int i = 0; i < list.length; i++) {
list[i] = new ArrayList<>();
}
//3. Traverse the source data and classify the data
for (int i = 0; i < arr.length; i++) {
list[(arr[i] - min) / arr.length].add(arr[i]);
}
//4. Sort each bucket
for (int i = 0; i < list.length; i++) {
list[i].sort(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o1 - o2;
}
});
// System.out.println("the" + (i+1) + "bucket:" + list [i] toString());
}
//5. Return the data in all buckets to the original array in turn
int index = 0; //Angle of original array
for (int i = 0; i < list.length; i++) {
for (int j = 0; j < list[i].size(); j++) {
arr[index++] = list[i].get(j);
}
}
// System.out.println(Arrays.toString(arr));
}
}
Count sort
thinking
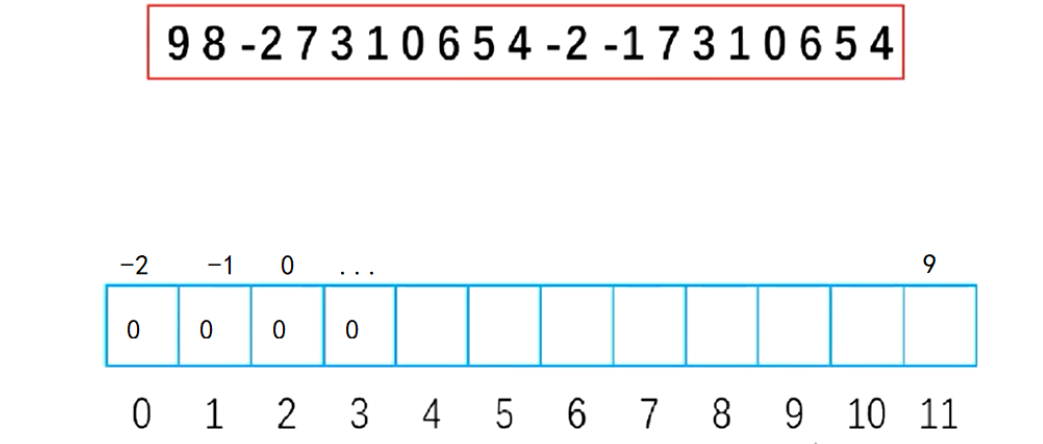
According to the maximum and minimum value of the array, determine an auxiliary array for counting. The length is the length of the original array. Each initial value is 0. The subscript of the auxiliary array corresponds to the number in the element group (find the corresponding relationship) - 2 corresponds to the position of 0. Therefore, there is an i+2 Relationship between the data and the subscript
Then start traversing the original array. When traversing to 9, add 1 to the subscript 11 of the auxiliary array and count
Finally, count the number of subscripts 0, that is - 2, in the auxiliary array, and then arrange
Count sort code
package p5.Sorting algorithm;
//Count sort
public class CountingSort extends Sort{
public CountingSort(int[] arr) {
super(arr);
}
@Override
public void sort() {
//1. Find the maximum and minimum values
int max = arr[0];
int min = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
if (arr[i] < min) {
min = arr[i];
}
}
//2. Determine the len gt h of the bucket, and determine the conversion relationship between data - > bucket corner mark and bucket corner mark - > data
//Create buckets (buckets are specifically used to count the number of occurrences of data)
int[] counts = new int[max - min + 1];
// index = num - min
// num = index + min
//3. Traverse the original array arr and count the number of occurrences of each data in the bucket
for (int i = 0; i < arr.length; i++) {
counts[arr[i] - min]++;
}
//4. Traverse the bucket and backfill each number to arr according to the number of occurrences from left to right
int k = 0;
for (int index = 0; index < counts.length; index++) {
for (int count = 0; count < counts[index]; count++) {
int num = index + min;
arr[k++] = num;
}
}
}
}
The above sorting algorithm is basically over
Next, test the execution time of all sorts
Sort test code
This part was also mentioned in the previous section, and the implementation will not be discussed in detail here
package p5.Sorting algorithm;
import java.util.Arrays;
import java.util.Random;
/*
Algorithm execution time
In addition to the strategy of the algorithm
It also has something to do with the data distribution
Data distribution:
Completely random, roughly ordered and roughly stable
Select 5 5 4
Bubbling 4 4 5
Insert 3 1 3
Hill 2 3 2
Merge 1 2 1
Single fast 1 + 3 + 1+
Double fast 1 + 1 + 1+
Three fast n n
Base row 3 - 4 3-
Bucket sorting 4 + 3 - 4+
Scheduling 1 + + 3 - 1++
*/
public class TestSort {
public static void main(String[] args) {
ArrayData data = new ArrayData(1);
int[] arr = data.makeData();
test01(arr);
test02(arr);
test03(arr);
test04(arr);
test05(arr);
test06(arr);
test07(arr);
test08(arr);
test09(arr);
test10(arr);
test11(arr);
}
private static void test11(int[] arr) {
CountingSort countingSort = new CountingSort(arr);
Long start = System.currentTimeMillis();
countingSort.sort();
Long end = System.currentTimeMillis();
System.out.println("Count sort:" + (end - start) + "ms");
}
private static void test10(int[] arr) {
BucketSort bucketSort = new BucketSort(arr);
Long start = System.currentTimeMillis();
bucketSort.sort();
Long end = System.currentTimeMillis();
System.out.println("Bucket sorting:" + (end - start) + "ms");
}
private static void test09(int[] arr) {
RadixSort radixSort = new RadixSort(arr);
Long start = System.currentTimeMillis();
radixSort.sort();
Long end = System.currentTimeMillis();
System.out.println("Cardinality sorting:" + (end - start) + "ms");
}
private static void test08(int[] arr) {
QuickSort03 quickSort03 = new QuickSort03(arr);
Long start = System.currentTimeMillis();
quickSort03.sort();
Long end = System.currentTimeMillis();
System.out.println("Three way fast platoon:" + (end - start) + "ms");
}
private static void test07(int[] arr) {
QuickSort02 quickSort02 = new QuickSort02(arr);
Long start = System.currentTimeMillis();
quickSort02.sort();
Long end = System.currentTimeMillis();
System.out.println("Two way fast exhaust:" + (end - start) + "ms");
}
private static void test06(int[] arr) {
QuickSort01 quickSort01 = new QuickSort01(arr);
Long start = System.currentTimeMillis();
quickSort01.sort();
Long end = System.currentTimeMillis();
System.out.println("Single way fast platoon:" + (end - start) + "ms");
}
private static void test05(int[] arr) {
MergeSort mergeSort = new MergeSort(arr);
Long start = System.currentTimeMillis();
mergeSort.sort();
Long end = System.currentTimeMillis();
System.out.println("Merge sort:" + (end - start) + "ms");
}
private static void test04(int[] arr) {
ShellSort shellSort = new ShellSort(arr);
Long start = System.currentTimeMillis();
shellSort.sort();
Long end = System.currentTimeMillis();
System.out.println("Hill sort:" + (end - start) + "ms");
}
private static void test03(int[] arr) {
InsertionSort insertionSort = new InsertionSort(arr);
Long start = System.currentTimeMillis();
insertionSort.sort();
Long end = System.currentTimeMillis();
System.out.println("Insert sort:" + (end - start) + "ms");
}
private static void test02(int[] arr) {
BubbleSort bubbleSort = new BubbleSort(arr);
Long start = System.currentTimeMillis();
bubbleSort.sort();
Long end = System.currentTimeMillis();
System.out.println("Bubble sort:" + (end - start) + "ms");
}
private static void test01(int[] arr) {
SelectionSort selectionSort = new SelectionSort(arr);
Long start = System.currentTimeMillis();
selectionSort.sort();
Long end = System.currentTimeMillis();
System.out.println("Select sort:" + (end - start) + "ms");
}
}
test data
This is only the test data on my computer and does not represent a certain execution speed, but it can be seen that there will be a gap in execution time with different sorting and different data
The array data of each test is the same
The contents of the array are completely random
The numbers in the array are completely random
First test
Select sort: 181ms
Bubble sorting: 129ms
Insert sort: 14ms
Hill sort: 4ms
Merge sort: 4ms
Single way fast platoon: 3ms
Two way fast platoon: 3ms
Three way fast platoon: 4ms
Cardinality sorting: 14ms
Bucket sorting: 46ms
Counting and sorting: 1ms
Second test
Select sort: 184ms
Bubble sorting: 126ms
Insert sort: 18ms
Hill sort: 3ms
Merge sort: 3ms
Single way fast platoon: 3ms
Two way fast platoon: 3ms
Three way fast platoon: 4ms
Cardinality sorting: 15ms
Bucket sorting: 53ms
Counting and sorting: 1ms
Third test
Selection sort: 185ms
Bubble sorting: 116ms
Insert sort: 16ms
Hill sort: 3ms
Merge sort: 3ms
Single way fast platoon: 2ms
Two way fast platoon: 3ms
Three way fast platoon: 2ms
Cardinality sorting: 11ms
Bucket sorting: 54ms
Counting and sorting: 1ms
The contents of the array are roughly ordered
The data in the array increases or decreases as a whole
First test
Selection sort: 91ms
Bubble sorting: 25ms
Insert sort: 0ms
Hill sort: 3ms
Merge sort: 2ms
Single way fast platoon: 3ms
Two way fast platoon: 2ms
Three way fast platoon: 4ms
Cardinality sorting: 20ms
Bucket sorting: 6ms
Count sorting: 9ms
Second test
Selection sort: 112ms
Bubble sorting: 22ms
Insert sort: 0ms
Hill sort: 3ms
Merge sort: 3ms
Single way fast platoon: 4ms
Two way fast platoon: 2ms
Three way fast platoon: 3ms
Cardinality sorting: 23ms
Bucket sorting: 6ms
Counting and sorting: 10ms
Third test
Selection sort: 107ms
Bubble sorting: 33ms
Insert sort: 0ms
Hill sort: 2ms
Merge sort: 3ms
Single way fast platoon: 3ms
Two way fast platoon: 2ms
Three way fast platoon: 4ms
Cardinality sorting: 16ms
Bucket sorting: 5ms
Counting and sorting: 10ms
The contents of the array are roughly stable
The data in the array fluctuates in a range as a whole
First test
Selection sorting: 120ms
Bubble sorting: 141ms
Insert sort: 16ms
Hill sort: 3ms
Merge sort: 4ms
Single way fast platoon: 3ms
Two way fast platoon: 3ms
Three way fast platoon: 3ms
Cardinality sorting: 15ms
Bucket sorting: 45ms
Counting and sorting: 1ms
Second test
Selection sort: 108ms
Bubble sorting: 137ms
Insert sort: 19ms
Hill sort: 3ms
Merge sort: 3ms
Single way fast platoon: 3ms
Two way fast platoon: 2ms
Three way fast exhaust: 1ms
Cardinality sorting: 14ms
Bucket sorting: 48ms
Count sorting: 0ms
Third test
Selection sort: 108ms
Bubble sorting: 119ms
Insert sort: 21ms
Hill sort: 3ms
Merge sort: 3ms
Single way fast platoon: 3ms
Two way fast platoon: 3ms
Three way fast platoon: 3ms
Cardinality sorting: 16ms
Bucket sorting: 47ms
Counting and sorting: 1ms
lookup
Binary search
As mentioned earlier, I won't repeat it here
(4 messages) algorithm 1: divide and conquer backtracking_ Ningmengyouzhi's blog - CSDN blog
Interpolation search
For binary search, we will consider such a problem. Here is a dictionary for you to find about. How do you find it? Is it also a two-point from the middle? Obviously not
So for this kind of sequential and evenly distributed data, we can divide it in proportion or four
Six. This fraction is based on the given data
For example, data: 2 4 6 8 10 12 14 16 18 20
If you are asked to find 4, how should you divide it?
4 - 2 = 2
20 - 2 = 18
2 / 18 = 1 / 9
(9 - 0)*(1/9)= 1
That is, this time, the mid = 1. Our data score is very average, so we found it at one time
Summary formula: Mid = Low + (key - a [Iow]) / (a [high] - a [low]) * (high low)
Compared with binary search, interpolation search is the difference in this place;
Due to the difference ratio of this place, another difference is the condition that can not be found
One possibility is low > high
Another possibility is that due to this formula, the mid may eventually exceed the array subscript (out of bounds) when it does not exist
For example, 1 2 3 4 5 6
If you are asked to find 1000, the mid will cross the border and cannot be found (this place may not be figured out for a while, so you can understand it by giving more examples)
Other places are basically similar to binary search
Interpolation lookup code
package p5.Sorting algorithm;
//Find interpolation
public class InterpolationSearch {
public static void main(String[] args) {
// int[] arr = {-12,-10,-6,-2,0,2,6,8,12,14,18,22,25,26,30,33,38,40};
int[] arr = {-1000,-500,-2,0,50,51,52,54,55,90,1500,4000,8000,10000};
int key = 55;
int index = interpolationSearch(arr,0, arr.length - 1,key);
System.out.println("index:" + index);
System.out.println(count);
count = 0;
index = binarySearch(arr,0,arr.length - 1,key);
System.out.println("index:" + index);
System.out.println(count);
}
private static int binarySearch(int[] arr, int min, int max, int key) {
count++;
if (min > max) {
return -1;
}
int mid = (min + max) / 2;
if (arr[mid] == key) {
return mid;
} else if (key < arr[mid]) {
return binarySearch(arr,min,mid - 1,key);
} else {
return binarySearch(arr,mid + 1,max,key);
}
}
private static int count = 0;
private static int interpolationSearch(int[] arr, int low, int high, int key) {
count++;
if (low > high) {
return -1;
}
int mid = low + (int) (1.0 * (key - arr[low]) / (arr[high] - arr[low]) * (high - low));
if (mid < low || mid > high) {
return -1;
}
if (arr[mid] == key) {
return mid;
} else if (key < arr[mid] ) {
return interpolationSearch(arr,low,mid - 1,key);
} else {
return interpolationSearch(arr,mid + 1, high,key);
}
}
}
Then some sorting and searching of the algorithm will come to an end for the time being.