This question comes from the third question of the 251th round of force deduction competition. The difficulty is medium. Investigate the backtracking method or KM algorithm
Title: maximum compatibility score
There is a questionnaire composed of n questions. The answer to each question is either 0 (no), or 1 (yes).
The questionnaire was distributed to m students and M tutors whose numbers ranged from 0 to m - 1. Students' answers are represented by a two-dimensional integer array students, where students[i] is an integer array containing the answers given by the ith student to the questionnaire (subscript starts from 0). The tutor's answer is represented by a two-dimensional integer array mentors, where mentors[j] is an integer array containing the answers given by the jth tutor to the questionnaire (subscript starts from 0).
Each student is assigned to a tutor, and each tutor is assigned to a student. The compatibility score between paired students and tutors is equal to the number of times students and tutors answer the same.
For example, if the student's answer is [1, 0, 1] and the tutor's answer is [0, 0, 1], their compatibility score is 2, because only the second and third answers are the same.
Please find out the best matching scheme between students and tutors to maximize compatibility and score.
Give you students and participants, and return the maximum compatibility score and.
Example
Example 1:
Input: students = [[1,1,0], [1,0,1], [0,0,1]], participants = [[1,0,0], [0,0,1], [1,1,0]]
Output: 8
Explain: assign students and mentors as follows:
-Student 0 is assigned to tutor 2 with a compatibility score of 3.
-Student 1 is assigned to tutor 0 with a compatibility score of 2.
-Student 2 is assigned to tutor 1 with a compatibility score of 3.
The maximum compatibility score sum is 3 + 2 + 3 = 8.
Example 2:
Input: students = [[0,0], [0,0], [0,0]], participants = [[1,1], [1,1], [1,1]]
Output: 0
Explanation: the compatibility score of any student paired with tutor is 0.
Tips:
- m == students.length == mentors.length
- n == students[i].length == mentors[j].length
- 1 <= m, n <= 8
- students[i][k] is 0 or 1
- mentors[j][k] is 0 or 1
Problem solving ideas
There is no doubt that this is a problem of finding the optimal solution. Students and tutors correspond one by one. If greedy strategy is used, it may not be the optimal solution. First, the data can be processed in one step, and the two-dimensional arrays of m*n can be transformed into m*m matrix scores. The value scores[i][j] of the element represents the same number of questions when the ith student matches the jth tutor, and then the problem is regarded as the following description:
For an M*M integer matrix, find the maximum value of the sum of any m elements. It is required that the row and column of each element are not repeated.
For this problem, it can be seen intuitively that the conditions are similar to the well-known eight queens algorithm, so the first reaction will be to choose the backtracking method to solve it. However, the disadvantages of backtracking method are also obvious. If the M value of the problem is too large, it will lead to very high time complexity. In fact, this kind of problem can be regarded as the maximum matching problem of bipartite graph, so there is a more ingenious solution: KM algorithm (advanced version of Hungarian algorithm to realize the optimal matching of weighted bipartite graph)
Backtracking method
We should basically know the backtracking method. We all know its template after class. We can finish it directly~
class Solution {
private int ans = 0;
public int maxCompatibilitySum(int[][] students, int[][] mentors) {
int m = students.length;
int n = students[0].length;
int[][] scores = new int[m][m];
for (int i = 0; i < m; i++) {
for (int j = 0; j < m; j++) {
for (int k = 0; k < n; k++) {
scores[i][j] += students[i][k] == mentors[j][k] ? 1 : 0;
}
}
}
boolean[] visited = new boolean[m];
dfs(m, scores, 0, 0, visited);
return ans;
}
private void dfs(int m, int[][] scores, int i, int sum, boolean[] visited) {
if (i >= m) {
ans = Math.max(ans, sum);
} else {
for (int j = 0; j < m; j++) {
if (visited[j]) continue;
visited[j] = true;
dfs(m, scores, i + 1, sum + scores[i][j], visited);
visited[j] = false;
}
}
}
}
Execution results:

KM algorithm
The time complexity of backtracking method (full array template) is O(m!), If it is not because the condition of this problem is m < = 8, it is basically unlikely to be submitted to pass... In contrast, the efficiency of KM algorithm will be relatively high. It gradually optimizes the optimal solution in recursion by setting expectations (also known as benchmarking). When the expectations cannot meet the optimization, it appropriately reduces the expectations, saving a lot of unnecessary operations like backtracking. Please analyze the specific km algorithm and Hungarian algorithm by yourself
class Solution {
public int maxCompatibilitySum(int[][] students, int[][] mentors) {
int m = students.length;
int n = students[0].length;
int[][] scores = new int[m][m];
for (int i = 0; i < m; i++) {
for (int j = 0; j < m; j++) {
for (int k = 0; k < n; k++) {
scores[i][j] += students[i][k] == mentors[j][k] ? 1 : 0;
}
}
}
return KM(m, scores);
}
/** KM algorithm */
private int KM(int m, int[][] scores) {
int[] match = new int[m]; //Mapping: mentor - > matching student s
int[] sExcept = new int[m]; //student expectations
int[] mExcept = new int[m]; //Expected value of mentor
for (int i = 0; i < m; i++) {
match[i] = -1; //Initialize to - 1
for (int j = 0; j < m; j++) {
sExcept[i] = Math.max(sExcept[i], scores[i][j]); //Maximize student s' expectations
}
}
for (int i = 0; i < m; i++) {
while (true) {
boolean[] sVisited = new boolean[m]; //Filter matched student s
boolean[] mVisited = new boolean[m]; //Filter matched mentor s
if (dfs(i, m, scores, match, sExcept, mExcept, sVisited, mVisited)) break;
for (int j = 0; j < m; j++) {
if (sVisited[j]) sExcept[j]--;
if (mVisited[j]) mExcept[j]++;
}
}
}
int ans = 0;
for (int i = 0; i < m; i++) {
ans += scores[match[i]][i];
}
return ans;
}
/** hungarian algorithm */
private boolean dfs(int i, int m, int[][] scores, int[] match, int[] sExcept, int[] mExcept, boolean[] sVisited, boolean[] mVisited) {
sVisited[i] = true;
for (int j = 0; j < m; j++) {
if (mVisited[j]) continue;
int temp = scores[i][j] - sExcept[i] - mExcept[j];
if (temp >= 0) {
mVisited[j] = true;
if (match[j] == -1 || dfs(match[j], m, scores, match, sExcept, mExcept, sVisited, mVisited)) {
match[j] = i;
return true;
}
}
}
return false;
}
}
Execution results:
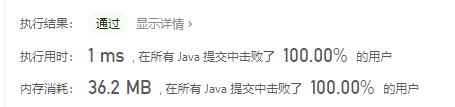
summary
The comparison of the results is obvious. When the problem scale is large, the efficiency of KM algorithm will be significantly better than that of ordinary backtracking algorithm. If the scale limit is higher, this is a middle problem.