My solution
/**
* 2ms 21.07
* 41M 33.17
* It's actually breadth first search
* The entry point is to see layer by layer, and build the next layer according to the current layer.
* */
public static int maxDepth(TreeNode root) {
if (null == root) {
return 0;
}
int deep = 1;
List<TreeNode> curLevel = new ArrayList<>();
curLevel.add(root);
List<TreeNode> nextLevel = null;
while (hasNextLevel(curLevel)) {
nextLevel = new ArrayList<>();
for (TreeNode cur : curLevel) {
if (null != cur) {
nextLevel.add(cur.left);
nextLevel.add(cur.right);
}
}
curLevel = nextLevel;
deep ++;
}
return deep;
}Official - breadth first search
/**
* Official breadth first search
* Queue @see MyQueue is used
* */
public static int maxDepth_l1(TreeNode root) {
if (null == root) {
return 0;
}
Queue<TreeNode> curLevel = new LinkedList<>();
curLevel.offer(root);
int deep = 0;
while (!curLevel.isEmpty()) {
int size = curLevel.size();//TODO fixed poll times
while (size > 0) {
TreeNode curNode = curLevel.poll();
if (curNode == null) {
continue;
}
if (curNode.left != null) {
curLevel.offer(curNode.left);
}
if (curNode.right != null) {
curLevel.offer(curNode.right);
}
size --;
}
// Queue<TreeNode> curLevelTemp = curLevel;
// for (TreeNode cur : curLevelTemp) {java.util.ConcurrentModificationException
// if (cur == null) {
// continue;
// }
// if (cur.left != null) {
// curLevel.offer(cur.left);
// }
// if (cur.right != null) {
// curLevel.offer(cur.right);
// }
// curLevel.poll();
// }
deep ++;
}
return deep;
}Official - depth first search
/**
* Official depth first search
* Using recursion
* If we know the maximum depth l and r of the left and right subtrees, the maximum depth of the binary tree is
*
* max(l,r) + 1
*
* The maximum depth of the left subtree and the right subtree can be calculated in the same way.
* */
public static int maxDepth_l2(TreeNode root) {
// 3
// / \
// 9 20
// / \
// 15 7
if (root == null) {
return 0;
} else {
int maxLeft = maxDepth_l2(root.left);//1
int maxRight = maxDepth_l2(root.right);
return Math.max(maxLeft, maxRight) + 1;
}
}Expansion DFS & BFS
Depth first search algorithm DFS
1. Algorithm steps:
——Access vertex v;
——Starting from the unreachable adjacency points of v, the depth first traversal of the graph is carried out; The vertices of the graph are accessed until they are all connected;
——If there are still vertices in the graph that have not been accessed at this time, start from a vertex that has not been accessed and repeat the depth first traversal until all vertices in the graph have been accessed
2. DFS belongs to blind search. Depth first search is a classical algorithm in graph theory. Using depth first search algorithm can generate the corresponding topological sorting table of the target graph. Using topological sorting table can easily solve many related graph theory problems, such as maximum path problem and so on. Generally, heap data structure is used to assist in the implementation of DFS algorithm.
Breadth first search algorithm BFS
1. Algorithm steps:
——First, put the root node into the queue;
——Take the first node from the queue and verify that it is the target. If the target is found, the search is ended and the result is returned. Otherwise, all its direct child nodes that have not been verified will be added to the queue;
——If the queue is empty, it means that the whole graph has been checked - that is, there is no target to search in the graph. End the search and return "target not found";
——Repeat step 2
2. BFS also belongs to blind search. In short, BFS starts from the root node and traverses the nodes of the tree (graph) along the width of the tree (graph). If all nodes are accessed, the algorithm aborts. Generally, queue data structure is used to assist in the implementation of BFS algorithm.
Expand API queue
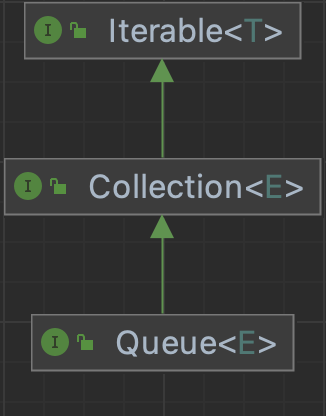
characteristic
1. Linear table / linear queue
2,FIFO
3. Out at the head and add at the end
implements
Queue<String> queue_ArrayBlockingQueue = new ArrayBlockingQueue<>(10);
Queue<String> queue_ArrayDeque = new ArrayDeque<>();
Queue<String> queue_ConcurrentLinkedDeque = new ConcurrentLinkedDeque<>();
Queue<String> queue_LinkedBlockingDeque = new LinkedBlockingDeque<>();
Queue<String> queue_LinkedList = new LinkedList<>();methods
| method | characteristic |
|---|---|
| add | The end of the queue is inserted, and the IllegalStateException is thrown when the queue is full |
| offer | The end of the queue is inserted, and false is returned when the queue is full |
| remove | Remove and return the header element. When the queue is empty, throw NoSuchElementException |
| pool | Remove and return the header element. When the queue is empty, return null |
| element | View the queue header element. When the queue is empty, throw NoSuchElementException |
| peek | View the queue header element. When the queue is empty, null is returned |
code
public static void main(String[] args) {
Queue<String> queue_ArrayBlockingQueue = new ArrayBlockingQueue<>(10);
Queue<String> queue_ArrayDeque = new ArrayDeque<>();
Queue<String> queue_ConcurrentLinkedDeque = new ConcurrentLinkedDeque<>();
Queue<String> queue_LinkedBlockingDeque = new LinkedBlockingDeque<>();
Queue<String> queue_LinkedList = new LinkedList<>();
System.out.println("++++++++++++++++++++++++++");
//add table footer - > [1,2,3]
//Throw IllegalStateException when the queue is full
Queue<Integer> queue_add = new ArrayBlockingQueue<>(2);
queue_add.add(1);
queue_add.add(2);
try {
queue_add.add(3);
} catch (Exception e) {
System.out.println(e);
}
for (Integer q : queue_add) {
System.out.println(q);
}
try {
Queue<Integer> queue_LinkedList_add = new LinkedList<>();
for (int i = 0; i < 1000000; i++) {
queue_LinkedList_add.add(i);
}
System.out.println(queue_LinkedList_add.size());
} catch (Exception e) {
System.out.println(e);
}
System.out.println("++++++++++++++++++++++++++");
//Footer of offer table - > [1,2,3,4,5,6]
//When the queue is full, false is returned
Queue<Integer> queue_offer = new ArrayBlockingQueue<>(4);
System.out.println(queue_offer.offer(1));
System.out.println(queue_offer.offer(2));
System.out.println(queue_offer.offer(3));
System.out.println(queue_offer.offer(4));
try {
System.out.println(queue_offer.offer(5));
} catch (Exception e) {
System.out.println(e);
}
for (Integer q : queue_offer) {
System.out.println(q);
}
try {
Queue<Integer> queue_LinkedList_offer = new LinkedList<>();
for (int i = 0; i < 1000000; i++) {
if (!queue_LinkedList_offer.add(i)) {
System.out.println("offer false");
}
}
System.out.println(queue_LinkedList_offer.size());
} catch (Exception e) {
System.out.println(e);
}
System.out.println("++++++++++++++++++++++++++");
//remove removes and returns the queue header element
//Throw NoSuchElementException when the queue is empty
Queue<Integer> queue_LinkedList_remove = new LinkedList<>();
for (int i = 0; i < 6; i++) {
queue_LinkedList_remove.offer(i);
}
for (int i = 0; i < 7; i++) {
try {
System.out.println(queue_LinkedList_remove.remove());
} catch (Exception e) {
System.out.println(i + " e = " + e);
}
}
System.out.println("++++++++++++++++++++++++++");
//poll removes and returns the queue header element
//null is returned when the queue is empty
Queue<Integer> queue_poll = new LinkedList<>();
for (int i = 0; i < 10; i++) {
queue_poll.offer(i);
}
for (int i = 0; i < 11; i++) {
try {
System.out.println(queue_poll.poll());
} catch (Exception e) {
System.out.println(i + " e = " + e);
}
}
System.out.println("++++++++++++++++++++++++++");
//Element returns the queue header element
//Throw NoSuchElementException when the queue is empty
Queue<Integer> queue_element = new LinkedList<>();
queue_element.offer(1);
queue_element.offer(2);
System.out.println(queue_element.element());
System.out.println(queue_element.poll());
System.out.println(queue_element.element());
System.out.println(queue_element.poll());
try {
System.out.println(queue_element.element());
} catch (Exception e) {
System.out.println(e);
}
System.out.println("++++++++++++++++++++++++++");
//peek returns the queue header element
//null is returned when the queue is empty
Queue<Integer> queue_peek = new LinkedList<>();
for (int i = 0; i < 3; i++) {
queue_peek.offer(i);
}
for (int i = 0; i < 4; i++) {
try {
System.out.println(queue_peek.peek());
System.out.println(queue_peek.poll());
} catch (Exception e) {
System.out.println(i + " e = " + e);
}
}
System.out.println("++++++++++++++++++++++++++");
}