Chapter IV
Hashtable
A brief introduction to hash table
1) Hash table can be understood as a collection structure at the use level
2) If there is only key and no accompanying data value, you can use the HashSet structure (unorderderdedset in C + +)
3) If there are both key s and accompanying data value s, you can use the HashMap structure (unordered map in C + +)
4) Whether there is accompanying data or not is the only difference between HashMap and HashSet. The actual structure of the underlying is the same thing
5) Using the operations of hash table put, remove, put and get, it can be considered that the time complexity is O(1), but the constant time is relatively large
6) If the hash table is a basic type, it is internally passed by value, and the memory occupation is the size of this thing
7) If the hash table is not the basic type, it is passed internally by reference. The memory occupation is the size of the memory address of the hash table. It is related to the principle of the hash table,
The principle will be described in the chapter "data structures related to hash functions" of the promotion class
Ordered table
1) The ordered table can be understood as a set structure at the use level
2) If there is only key and no accompanying data value, you can use the TreeSet structure (called orderedset in C + +)
3) If there are both key s and accompanying data value s, you can use the TreeMap structure (called orderedmap in C + +)
4) Whether there is accompanying data or not is the only difference between TreeSet and TreeMap. The actual structure of the underlying is the same thing
5) The difference between an ordered table and a hash table is that an ordered table organizes key s in order, while a hash table does not organize at all
5) Red black tree, AVL tree, size balance tree and jump table all belong to ordered table structure, but the specific implementation of the bottom layer is different
6) If the items put into the ordered table are basic types, they are passed internally by value, and the memory occupation is the size of this item
7) If the object placed in the ordered table is not a basic type, a comparator must be provided. It is passed internally by reference. The memory occupation is the size of the object's memory address
8) No matter what the underlying implementation is, as long as it is an ordered table, it has the following fixed basic functions and fixed time complexity
Fixed operation of ordered table
- void put(K key, V value): add a (key, val ue) record to the table, or update the key record to value
- V get(K key): query value according to the given key and return it.
- void remove(K key): removes the record of the key
- boolean containskey(K key): ask whether there is a record about the key.
- K firstkey(): returns the leftmost (smallest) sorting result of all key values.
- K laskey(): returns the rightmost (largest) sorting result of all key values.
- K floatkey (k key): if a key has been stored in the table, the key is returned; Otherwise, it returns the previous key in the sorting results of all key values
- K ceilingKey(K key): if a key has been stored in the table, the key is returned; Otherwise, the sorting results of all key values are returned,
The last key.
All the above operation time complexity is 0 (logn), and N is the number of records contained in the ordered table
The principle of order table will be described in the chapter "detailed explanation of order table" of the promotion class
Note: there is no need to know the principle of ordered table and hash table in the process of a large number of questions. The questions that need to know the principle are difficult problems, and the medium difficulty will not involve the internal principle.
Linked list
node is returned after head changing, and void is returned without head changing

Topic 1
Reverse single linked list, double linked list.
[analysis]: analyze with a cur node and try to adjust the next or pre direction. It's a bit like exchanging values. Remember to move cur back to the end.
Topic 2
Leetcode.234 Whether it is a palindrome linked list.
written examination:
1) Stack
2) Speed pointer (grasp the boundary and note the leetcode problem solution), find the midpoint, just put the right side into the stack and pay attention to comparison.
interview:
1) Fast and slow pointer centering
2) Reverse the right half and compare it with the left one by one
3) Restore to the original linked list
Topic 3
Given a key, the linked list is less than on the left, equal to in, and greater than on the right.
written examination:
[analysis] store it in an array, partition it, and restore it back to the original linked list
interview:
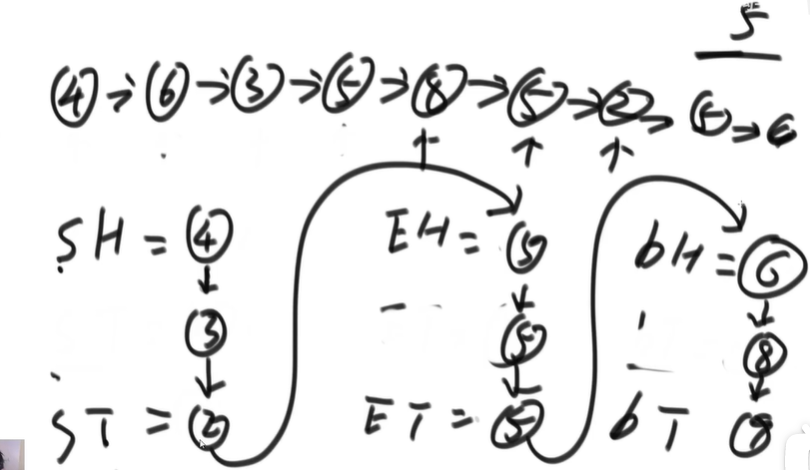
[analysis] define six pointers. Note that if there is no less than part, greater than part, equal to part.
Topic 4

written examination:
[analysis]: use hashmap to store the original node and its clone node. Just string the clone nodes together;
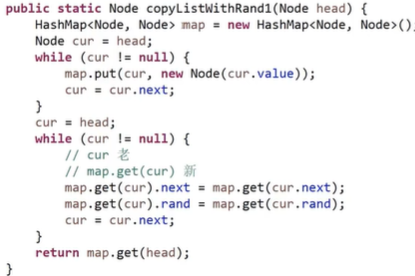
interview:
[analysis]:
1) First, connect the clone nodes behind the original node
2) Point the clone node rand pointer to the next node of its original node rand pointer
3) Separate linked list
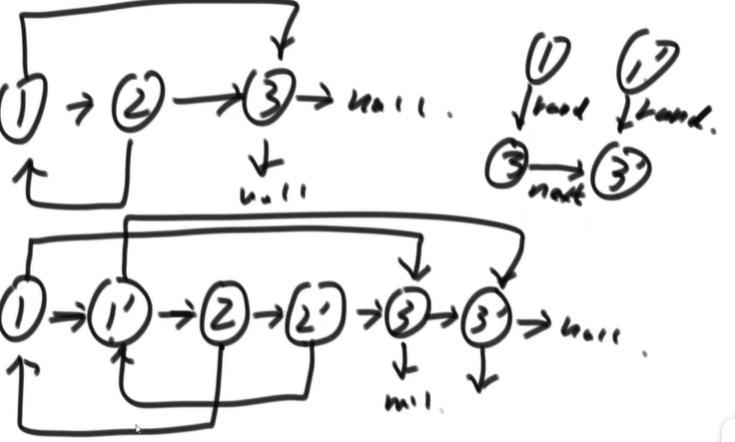
Topic 5 hard

Prove that a single linked list has a ring
1) Hash set
2) Speed pointer
1. Fast 2step, slow 1step. After the pointer meets,
2. Quickly return the pointer to the origin, and then everyone moves step by step. Meeting is the node entering the ring for the first time. (loop with ring returns to loop node, while loop without ring returns to null)
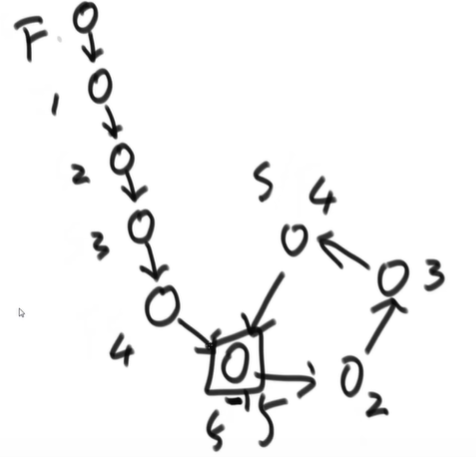
Due to the structure of the single linked list, the intersection of the two single linked lists must be combined, "Y" shape
Because of the structure of a single linked list, either both have rings or neither has rings, it is impossible for one to have a ring and one to have no ring
1) All acyclic
Let the long part be cut to the same length as the short part, and go together. If it is equal, it is the meeting node, and return to the meeting node loop
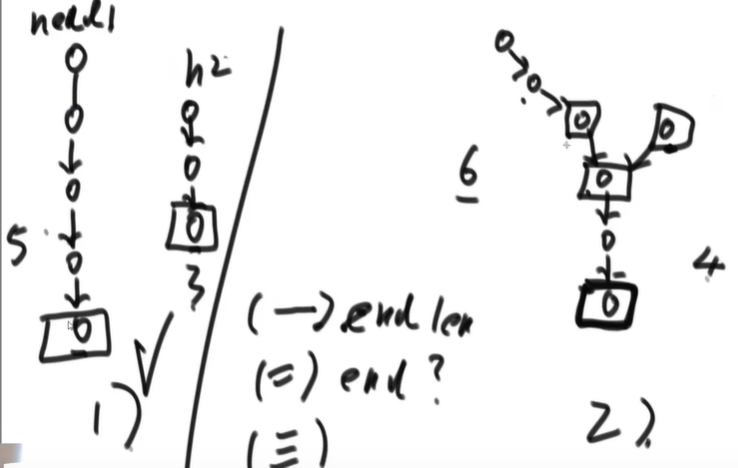
Let the parts of 6 and 4 be symmetrical and go down together. If they are equal, they will intersect
public static Node noLoop(Node head1, Node head2) {
if (head1 == null || head2 == null) {
return null;
}
Node cur1 = head1;
Node cur2 = head2;
int n = 0; //Use only one variable to record the difference between the lengths of the two linked lists
while (cur1.next != null) {
n++;
cur1 = cur1.next;
}
while (cur2.next != null) {
n--;
cur2 = cur2.next;
}
if (cur1 != cur2) {
return null;
}
//n: The length of linked list 1 minus the length of linked list 2
cur1 = n > 0 ? head1 : head2; //Who grows whose head becomes cur1
cur2 = cur1 == head1 ? head2 : head1; //Whose head is short becomes cur2
n = Math.abs(n);
while (n != 0) { //Go to the same length first
n--;
cur1 = cur1.next;
}
while (cur1 != cur2) {
cur1 = cur1.next;
cur2 = cur2.next;
}
return cur1;
}
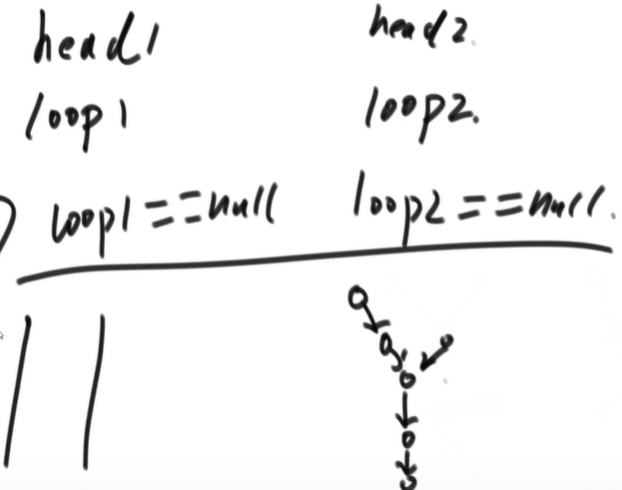
2) All have rings
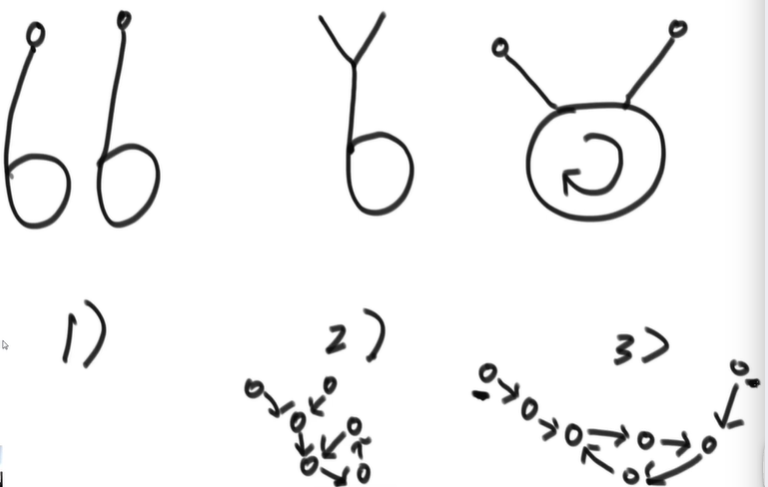
1) Do not intersect. Let loop1 go down until it returns to loop1 (turn around). If you encounter loop2, it is < 3 >, otherwise it is < 1 >.
2) loop1==loop2, let loop1 act as the end tail node in the acyclic case and perform the above operations.
3) Returns loop2 or loop1
public static Node bothLoop(Node head1, Node loop1, Node head2, Node loop2) {
Node cur1 = null;
Node cur2 = null;
if (loop1 == loop2) { //case2, refer to the above acyclic code
cur1 = head1;
cur2 = head2;
int n = 0;
while (cur1 != loop1) {
n++;
cur1 = cur1.next;
}
while (cur2 != loop2) {
n--;
cur2 = cur2.next;
}
cur1 = n > 0 ? head1 : head2;
cur2 = cur1 == head1 ? head2 : head1;
n = Math.abs(n);
while (n != 0) {
n--;
cur1 = cur1.next;
}
while (cur1 != cur2) {
cur1 = cur1.next;
cur2 = cur2.next;
}
return cur1;
}
else {//Case 1, 3
cur1 = loop1.next; //case3
while (cur1 != loop1) {// Turn around and come back
if (cur1 == loop2) {// If there is loop2 in the ring, there is case3,
return loop1;
}
cur1 = cur1.next;
}
return null;// case1
}
}
Chapter V
Recursive order
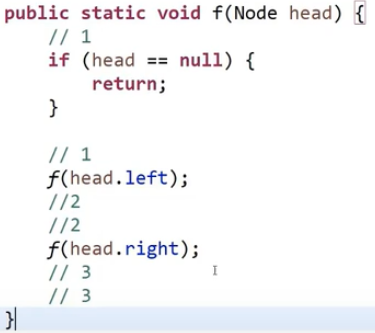
1) For the first time to the function body, -- > > pre order traversal:
2) Return to the function body for the second time, -- > > middle order traversal:
3) Return to the function body for the third time, -> > post order traversal:
Non recursive depth traversal (stack)
Preorder traversal
Print order: header - > left - > right
Illustration:
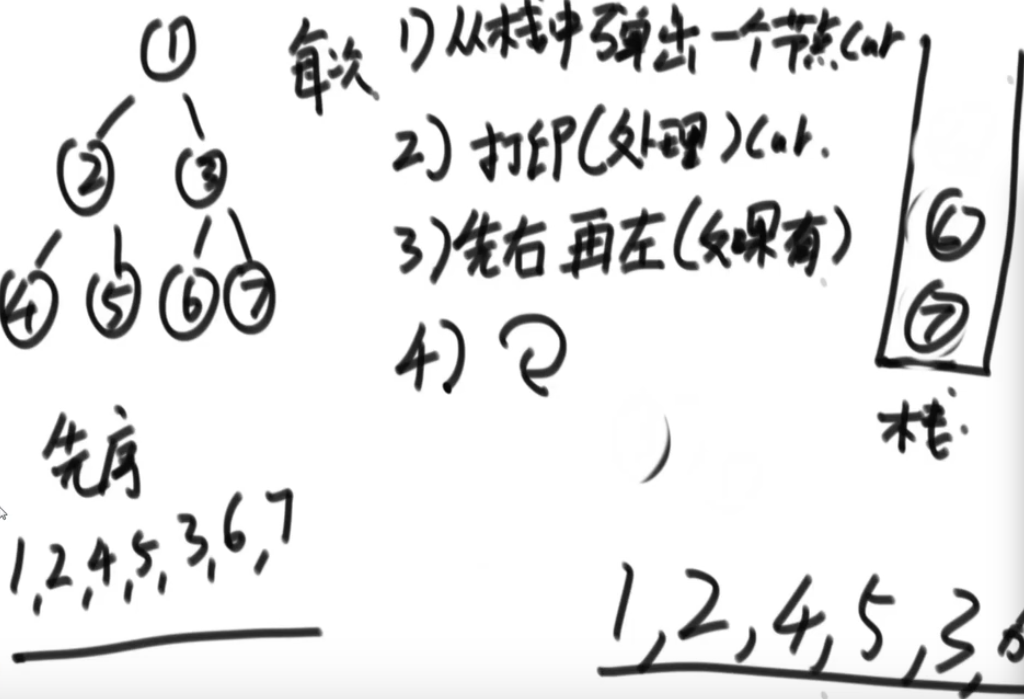
Pop up the stack first, right first and then left, (then pop up as left first and then right = = consistent with the original order)

Postorder traversal
The auxiliary stack is required in order to put it in the auxiliary stack in reverse order
Note: enter the stack left and right, exit the stack right and left


Medium order traversal

The left tree is all in at one time, then the cur node is processed, and then the right tree is repeated
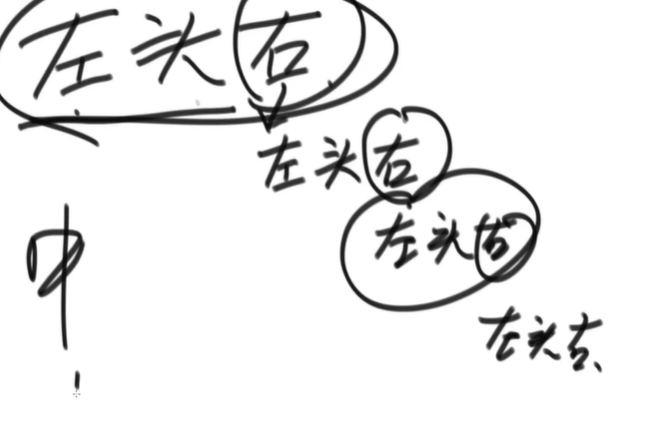
First left and then head, and then left and then head on the right tree

Breadth first traversal (queue)
Queue, pop up first, put left and then right
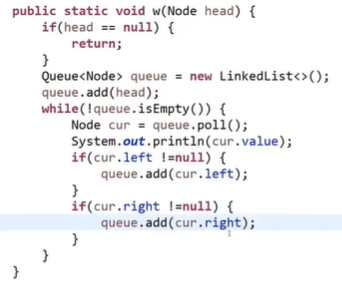
Topic 1
Find the maximum width of a binary tree
- HashMap
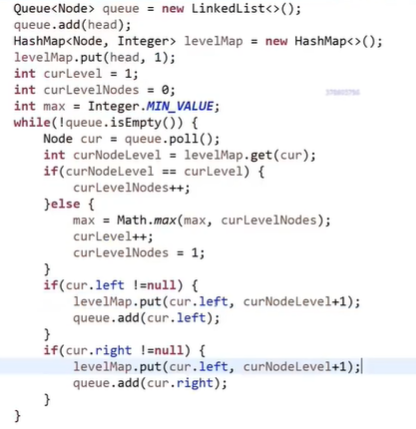
When the last one is finished, the team is empty, so it exits the loop, but the max and curLevel in if else are not updated.
while, add max = Math.max(max, curLevelNodes)
2. No hash table
NodeCurEnd, NodeNextEnd, CurLevel,max
class Solution {
public int widthOfBinaryTree(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
TreeNode curLevelEnd = root;//The last of the current layer
TreeNode nextLevelEnd = null;//The last one on the next floor
int curLevelNodes = 0;
int max = Integer.MIN_VALUE;//Return value
while( !queue.isEmpty() ){
root = queue.poll();//pop
System.out.print("\t" + root.val);
if(root.left!= null){//Always update the value of the next level
queue.add(root.left);
nextLevelEnd = root.left;
}
if(root.right!= null){
queue.add(root.right);
nextLevelEnd = root.right;
}
if(root != curLevelEnd){//Current last node not found
curLevelNodes++;//Number of nodes in the current layer++
}
else{
curLevelEnd = nextLevelEnd;//Enter the next layer and assign the value to the end node
nextLevelEnd = null;//Update the end node of the next layer and update max at the same time
max = max > curLevelNodes ? max : curLevelNodes+1;
curLevelNodes = 0;//After entering the next layer, the number of nodes in this layer is reset
}
}
return max;
}
}
Special binary tree
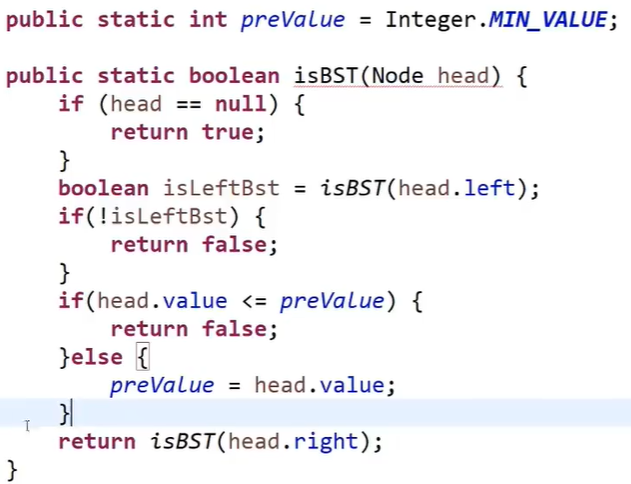
Search Binary Tree BST
Medium order traversal, ascending (not understood)

Complete binary tree
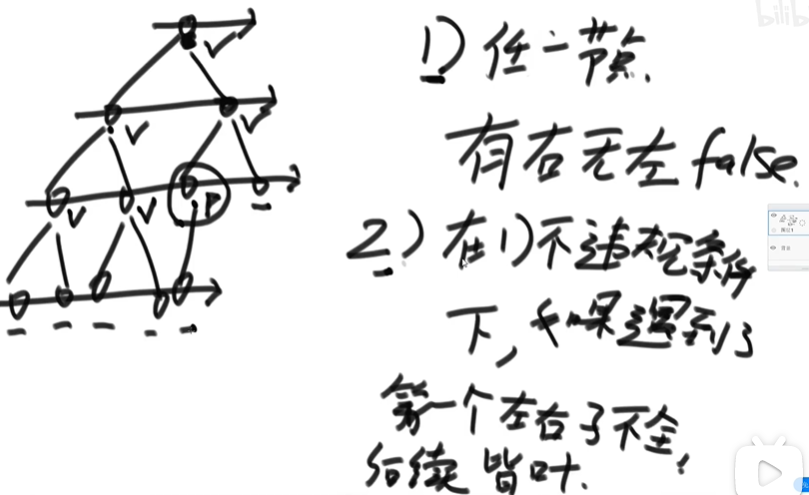
After the first node with a circle is encountered, the following nodes must be leaf nodes.
Full binary tree
The maximum depth d and the number of nodes n satisfy n=2^d-1
Balanced binary tree (summarize the routine of binary tree)
(the height difference between the left and right subtrees shall not exceed 1)
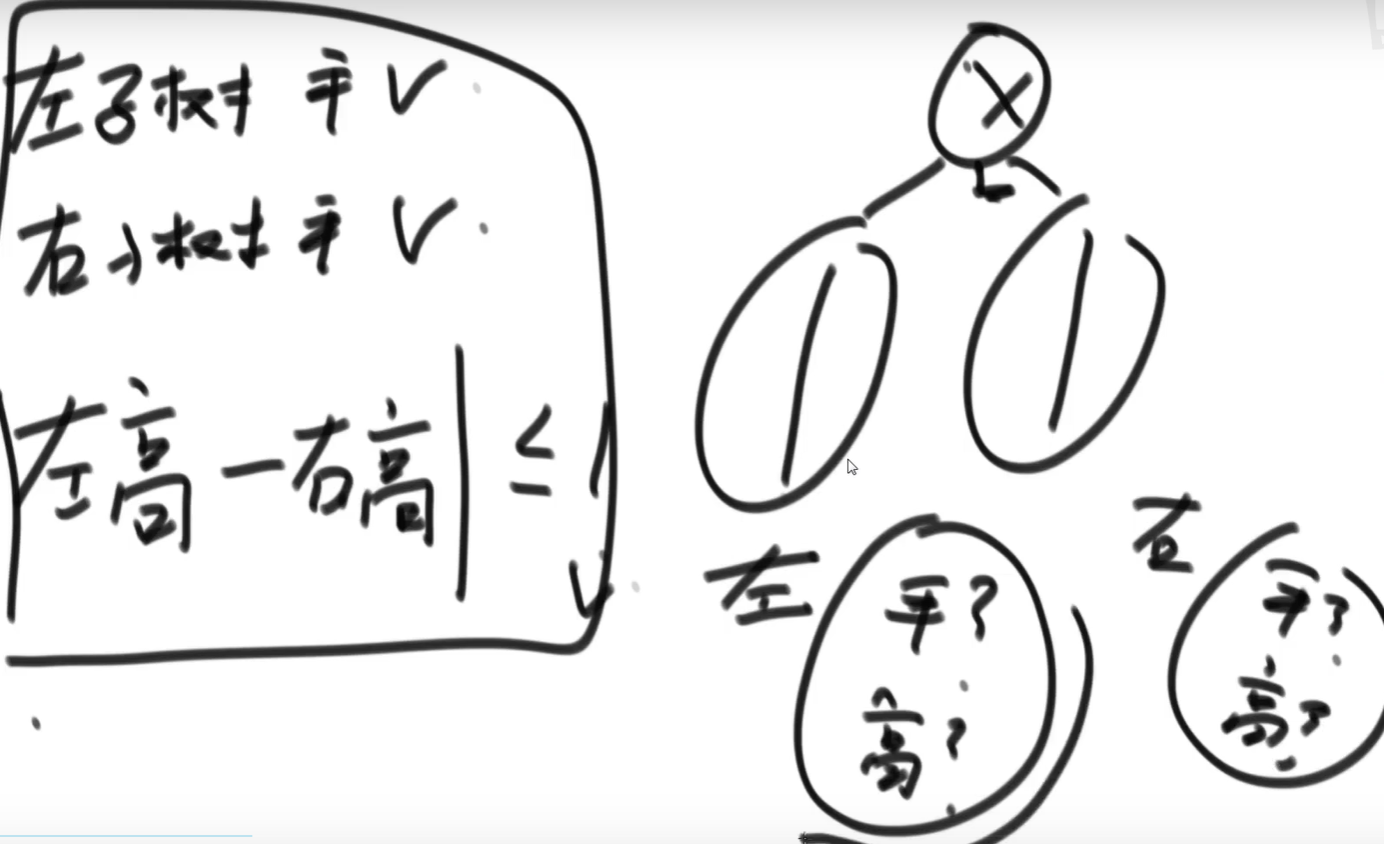
Routine: the left tree needs information (bool isBalanced, int high), the right tree needs information, and the intersection of three conditions is taken.
tricks
Routine (solve all tree DP, dynamic programming (the most difficult binary tree interview))
For: ask the left tree for information and the right tree for information to solve the problem
This routine cannot be solved by finding the median in the tree
The interview questions are designed to optimize, so it's easy to use.
1> BST
(left number BST)
&&Right number BST
&&Left Max < cur.val < right min)
!! Note: in the recursive routine, the returned items should be the same, so the left and right numbers should return three information (bool isBST, int max, int min)
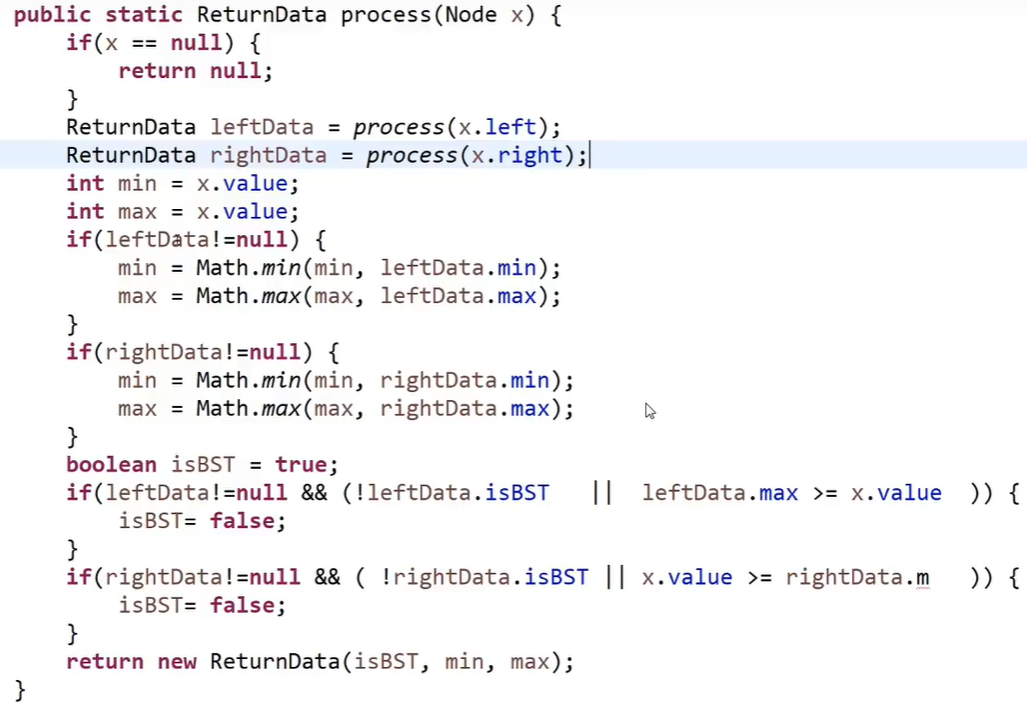
2> Full binary tree
(int height, int nodes)
Nodes = = (1 < < height) - 1 / / - has higher priority than < <
Topic 1
o1, o2 lowest common ancestor
1> HashMap(self, father)
Enter all nodes into HashMap first

Then use a HashSet to store the parent node path of o1 to the root node
Index the ancestor with o2 until there is a node that coincides with the parent node path (HashSet) of o1
2> Analysis:
1. o1 is directly the ancestor of o2, or o2 is directly the ancestor of o1.
2. o1 and o2 meet back
public static Node lowestAncestor(Node head, Node o1, Node o2) {
if (head == null || head == o1 || head == o2) {
return head;
}
Node left = lowestAncestor(head.left, o1, o2);//Lower left
Node right = lowestAncestor(head.right, o1, o2);//lower right
//Both left and right have return values, i.e. 2. Returns the current value
if (left != null && right != null) {
return head;
}
return left != null ? left : right;//Both the left and right numbers do not have return values, and the return value is not empty
}
Topic 2 successor nodes
There is one more parent attribute than an ordinary binary tree, and the parent of head is empty
The last node of the middle order traversal result is null
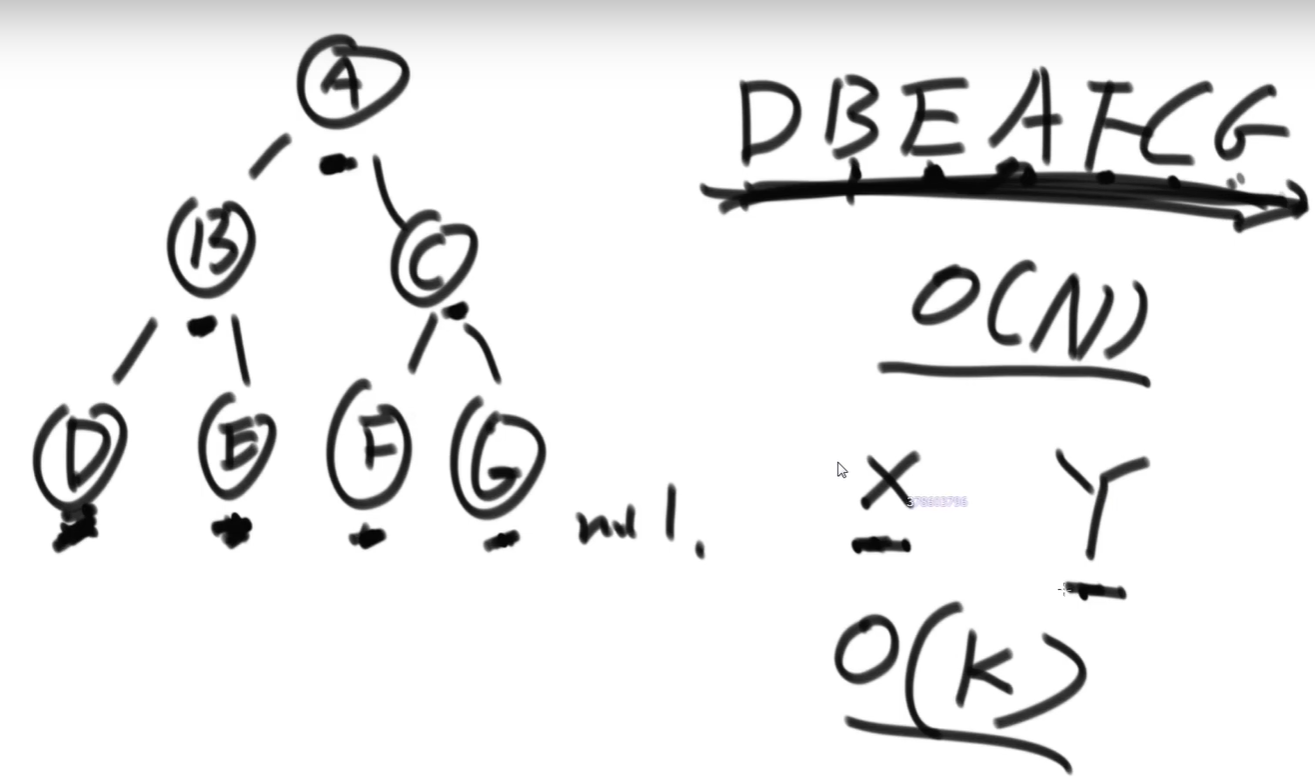
There is a right tree, = "find the one at the bottom left of the right number
If there is no right number, = "go back to become a left child and return to its parent node. (the rightmost one will not meet this condition, but the father of the head is just empty and will not be affected.)
Topic 3 serialization and deserialization
Traversing the tree,
//Serialization and deserialization of preorder traversal
//serialize
public static String serialByPre(Node head) {
if (head == null) {//#--Null,! -- split, value -- value
return "#!";
}
String res = head.value + "!";
res += serialByPre(head.left);
res += serialByPre(head.right);
return res;
}
//Deserialize. Split
public static Node reconByPreString(String preStr) {
String[] values = preStr.split("!");
Queue<String> queue = new LinkedList<String>();
for (int i = 0; i != values.length; i++) {
/*offer,add; poll,remove; peek,element
The former returns null, while the latter is abnormal
*/
queue.offer(values[i]);
}
return reconPreOrder(queue);
}
//Deserialization
public static Node reconPreOrder(Queue<String> queue) {
String value = queue.poll();
if (value.equals("#")) {
return null;
}
Node head = new Node(Integer.valueOf(value));
head.left = reconPreOrder(queue);
head.right = reconPreOrder(queue);
return head;
}
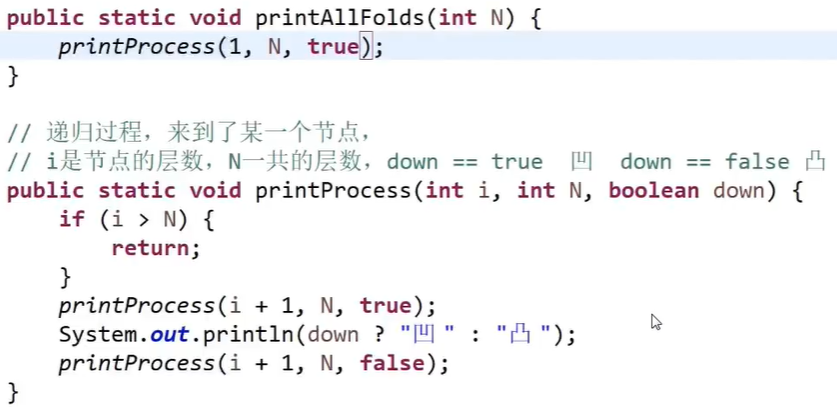
Topic 4 origami problem
Print crease direction = concave, convex
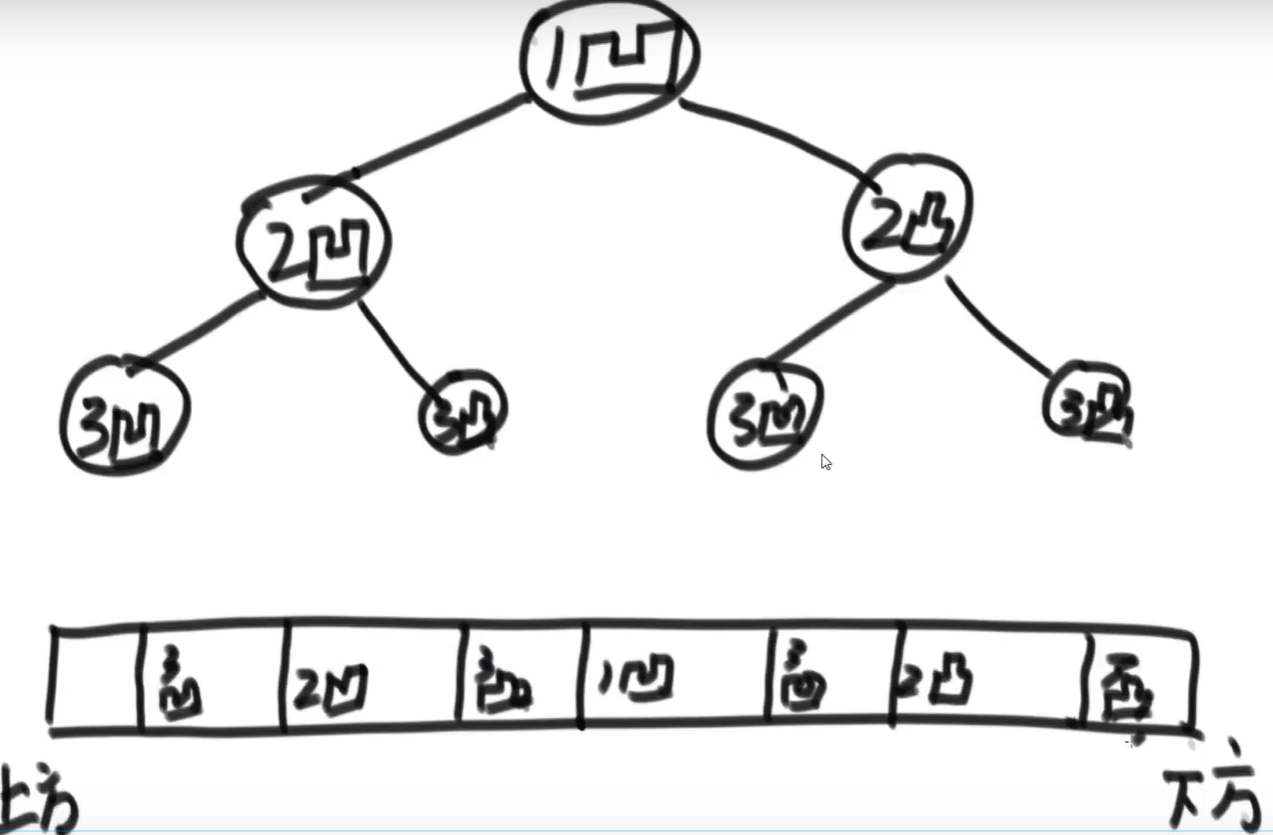
Middle order traversal
//space