- This article has a total of about 10000 words and takes about 40 minutes to read.
preface
Last note Tarjan's algorithm notes talk about the algorithms for finding cut points and cut edges in undirected graphs. This note will introduce the theoretical algorithm for finding strongly connected components in directed graphs.
In most cases, the algorithm of strongly connected component will not be directly examined in OI, but it has a wide range of other uses: for example, in some dp problems, it is necessary to shrink a ring directed graph into points one by one to become a DAG (directed acyclic graph), and then perform topological sorting. This paper not only introduces the strongly connected component, but also introduces the method of realizing the above steps - shrinking point.
By the way, shrinking point is really disgusting. After writing the code, it's like a mouthful of old blood gushing out of QAQ
In addition, the author will also introduce another application of Tarjan algorithm, finding the LCA (nearest common ancestor) on the tree: using the multiplication method to find the preprocessing with the time complexity of \ (\ mathcal{O}(n\log n) \) and the online query of \ (\ mathcal{O}(\log n) \); If the Tarjan algorithm is used to calculate the LCA, the offline query of \ (\ Theta(n+q) \) can be realized. This is an excellent time complexity optimization.
Problem introduction
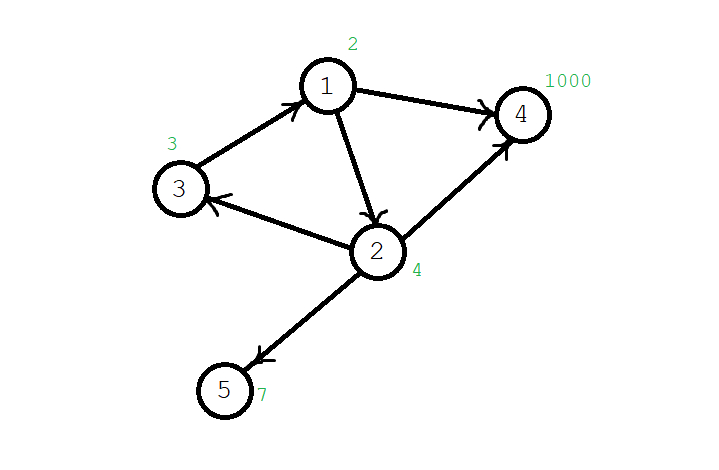
Little \ (P \) loves adventure. One day, he came to a huge tomb. There are \ (V \) rooms in this tomb, numbered \ (1,2,\cdots,V \), and there are treasures worth \ (a_i \) in the \ (I \) room. There are \ (|E124\) corridors connecting these \ (V \) rooms. However, the mechanism of the tomb is cleverly designed, and the corridor only allows one-way traffic. Now small \ (P \) can enter the tomb from any room or come out of any room.
Xiao \ (P \) can take all the treasures in his room when stealing the tomb and exploring the tomb, but if he repeatedly passes through a room, of course, there are no two treasures for him. So little \ (P \) wants to ask you, how much treasure can he take before leaving the exit?
Formally describe the topic: given a directed graph \ (G(V,E) \), point with weight, find a path to maximize the sum of node weights. You can pass through a point repeatedly, but the point weight is calculated only once.
For example, in the following figure, black numbers represent the room number and green represents the value of the treasure in the room. Small \ (P \) can take path 1 - > 2 - > 3 - > 1 - > 4, so the maximum value obtained is \ (a_1+a_2+a_3+a_4=2+3+4+1000=1009 \).
Tarjan finding strongly connected components
Ideas and steps of finding strongly connected components
Let's review the definition of strongly connected components:
In a directed graph, if we can find several nodes to form a point set \ (X \) so that these nodes can reach each other, the point set \ (X \) is called a connected component of the graph; Meanwhile, if there is no node \ (u\notin X \) for a connected component \ (X \), so that \ (X \) and \ (u \) still form connected components, then \ (X \) is called a strongly connected component of the graph.
(this concept seems a little awkward, but I don't know how to simply describe QwQ. I'm too konjac)
If Tarjan algorithm is used, all strongly connected components can still be found within the time complexity of \ (\ mathcal{O}(|V|+|E |). However, it is not the same as the algorithm for finding cut points and edges. We need to maintain the stack of the order in which a node is found. Its steps are as follows:
- Search from the source. When searching, put the searched nodes on the stack;
- Maintain the \ (\ textit{dfn} \) and \ (\ textit{low} \) values of the current node. Note that the maintenance method is different from the cut point and cut edge algorithms: if the node pointed to by the edge (V) of the current node \ (U \) is still in the stack, let \ (\ textit{low}[u]=\min(\textit{low}[u],\textit{low}[v]) \;
- Trace back when all outgoing edges of the current node have been searched (or the basic outgoing degree of the current node is \ (0 \)), but do not return to the stack.
- Until the \ (\ textit{low} \) value of the current backtracked node is equal to the \ (\ textit{dfn} \) value, dye the node with a color. At the same time, from the top of the stack to the node being ejected, each ejected node must be colored with the same color.
- After searching the whole graph, all nodes of the same color form a strongly connected component.
It seems that it's still not easy to understand QwQ? Let's take the following graph as an example to calculate all strongly connected components.
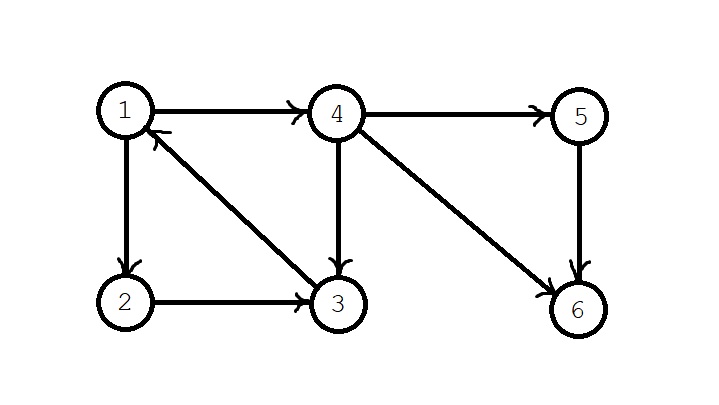
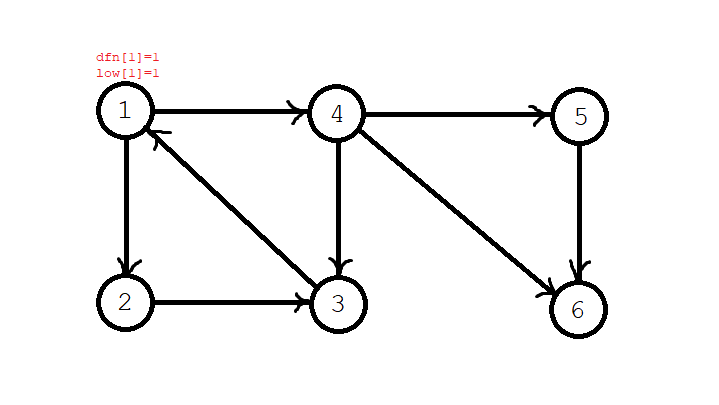
In the first step, we start searching from node 1, \ (\ textit{dfn}[1]=\textit{low}[1]=1 \), and the node \ (1 \) is stacked. Current stack sequence: \ (1 \);
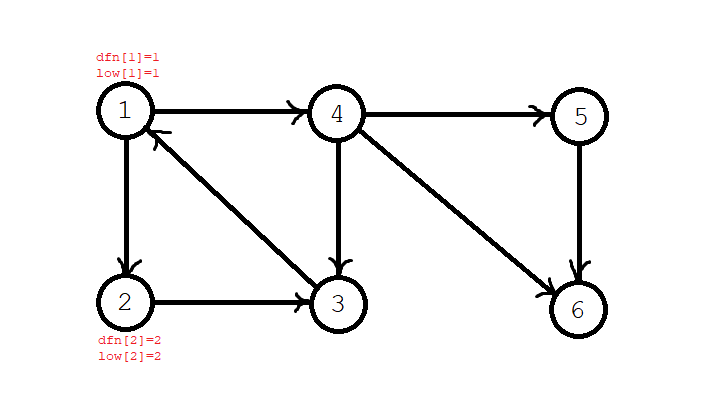
In the second step, we found node 2, and then \ (\ textit{dfn}[2]=\textit{low}[2]=2 \), node \ (2 \) is put into the stack. Current stack sequence: \ (1,2 \);
Step 3: when searching node 3, we find that node 3 can return to node \ (1 \), so \ (\ textit{dfn}[3]=3 \), \ (\ textit{low}[3]=\textit{low}[1]=1 \), node \ (3 \) is stacked, and the current stack sequence is \ (1,2,3 \).

The fourth step is backtracking, but because \ (\ textit{dfn} \) and \ (\ textit{low} \) of \ (3 \) are not equal, it means that it can return to a \ (1 \) node, which may form a strong connected component with the \ (1 \) node, so it does not back off the stack. Only update node \ (2 \), \ (\ textit{low}[2]=\min(\textit{low}[2], \textit{low}[3])=1 \). The stack sequence is still: \ (1,2,3 \).
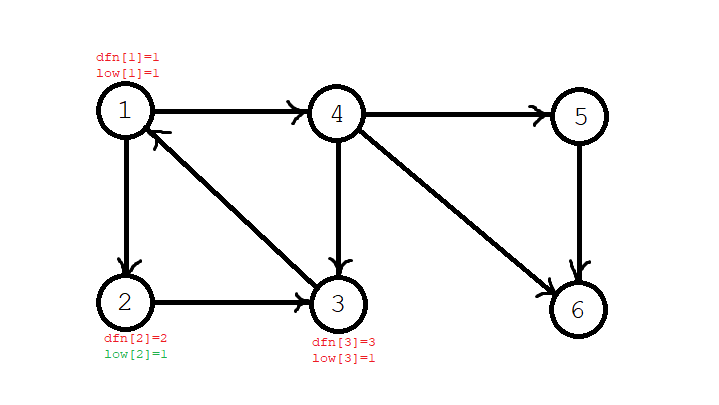
Step 5: search for node \ (4 \) and find that node \ (4 \) can reach node \ (3 \), so \ (\ textit{dfn}[4]=4 \), \ (\ textit{low}[4]=\textit{low}[3]=1 \), node \ (4 \) is stacked, and the current stack sequence is \ (1,2,3,4 \).
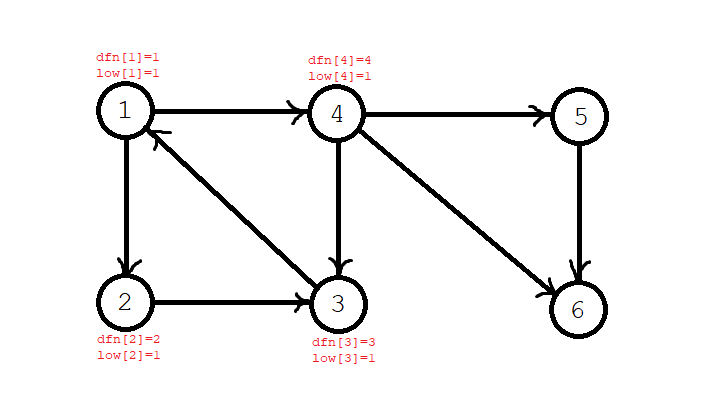
Step 6: search for the \ (5,6 \) node in sequence, \ (\ textit{dfn}[5]=\textit{low}[5]=5 \), \ (\ textit{dfn}[6]=\textit{low}[6]=6 \), the node \ (5,6 \) into the stack, and the current stack sequence \ (1,2,3,4,5,6 \).
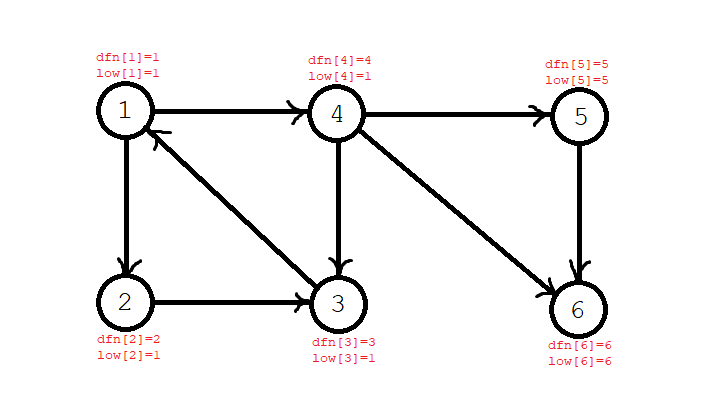
Step 7: it is found that the header has been searched. Backtracking, at this time \ (\ textit{low}[6]=\)\textit{dfn}[6] \ (, \) \ textit{low}[5]=\(\textit{dfn}[5] \) indicates that \ (6 \) and \ (5 \) form a separate strongly connected component, dye them, and return them to the stack. Current stack sequence: \ (1,2,3,4 \).
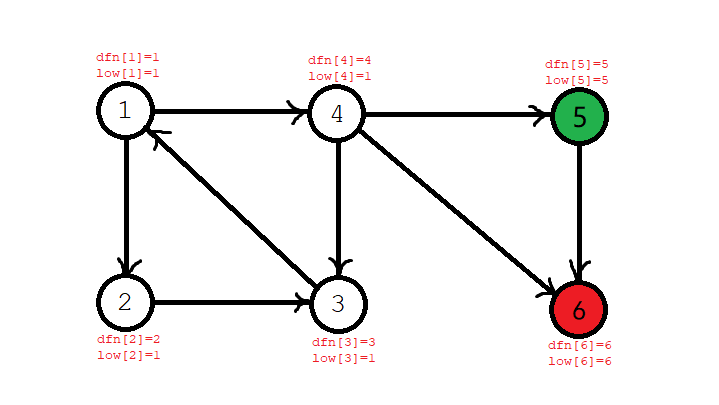
Next, go back to the \ (4 \) node. The \ (4 \) node found \ (6 \), but \ (6 \) is not in the stack, so it doesn't matter. Moreover, the \ (\ textit{low} \) value and \ (\ textit{dfn} \) value of \ (4 \) are not equal, so it's not back on the stack. The stack sequence is still: \ (1,2,3,4 \).
Tracing back to node \ (1 \), it is found that \ (\ textit{dfn}[1]=\textit{low}[1] \), so \ (1 \) is a root of strongly connected components. Pop up elements from the top of the stack until \ (1 \) is popped. At this time, dye all pop-up elements.
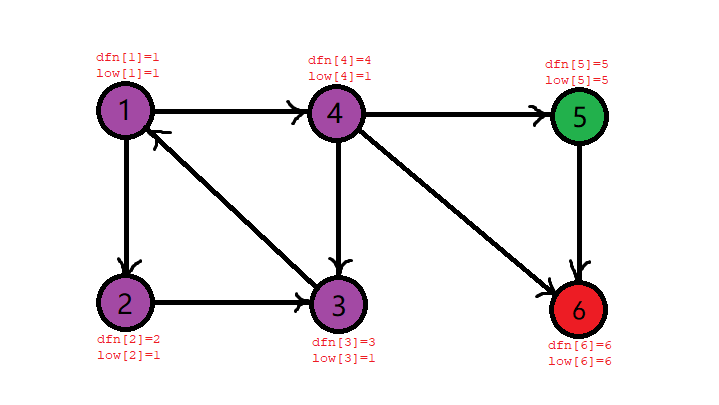
In this way, all nodes with the same color constitute a strongly connected component, and we find all the strongly connected components in the whole graph.
code
Still simulate the above steps:
#include <cstdio>
#include <stack>
using namespace std;
const int maxN = 2000001;
int top, n, m, cur, tot;
int head[maxN], dfn[maxN], low[maxN], color[maxN];
bool vis[maxN];
stack <int> stac; //STL is used here. If you want high performance, please use handwriting stack or O2 optimization
struct Edge {
int to;
int next;
} edge[maxN];
inline void add_edge(int u, int v) {
edge[++top].to = v;
edge[top].next = head[u];
head[u] = top;
}
void tarjan(int u) { //Tarjan finding strongly connected components
dfn[u] = low[u] = ++cur;
vis[u] = true;
stac.push(u); //Each time a new node is searched, it is stacked
for(int ptr = head[u]; ptr; ptr = edge[ptr].next) {
int curv = edge[ptr].to;
if(!dfn[curv]) {
tarjan(curv);
low[u] = min(low[u], low[curv]); //Update low value through child node
}
else if(vis[curv]) { //If the found node is not in the stack, it means that the node is already in the strongly connected component, and there is no need to update the low value
low[u] = min(low[u], low[curv]);
}
}
if(dfn[u] == low[u]) { //dfn[u] == low[u] means that this point is a strongly connected component, divided into a "root" node
color[u] = ++tot; //dyeing
vis[u] = false; //Back stack operation
while(stac.top() != u) {
color[stac.top()] = tot;
vis[stac.top()] = false;
stac.pop();
}
stac.pop();
}
}
int main(void) {
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; ++i) {
int ui, vi;
scanf("%d%d", &ui, &vi);
add_edge(ui, vi);
}
for(int i = 1; i <= n; ++i) {
if(!dfn[i]) { //A directed graph is not necessarily a strongly connected graph
tarjan(i);
}
}
for(int i = 1; i <= n; ++i) {
printf("%d ", color[i]); //Output the number of the strongly connected component where each point is located
}
return 0;
}
//by CaO
Shrinking point -- the reference of strongly connected components
Purpose of shrinking point
Back to the question in topic introduction:
If all the doors in the tomb in the title can't go back to the tomb that has passed, based on the greedy thought: we should choose to enter from the room without a room in front and leave from the room without a way - if you enter from a place with a room in front, why don't you enter in the previous room.
In this case, the first thing we think of is topological sorting: find the nodes with a penetration of \ (0 \) every time, delete these points, and search their "child" nodes in memory. (if I have time, I will open a pit and focus on topology sorting QwQ, but I'm still lazy now)
However, the problem does not guarantee that this graph is a DAG (directed acyclic graph). Therefore, if you use extension arrangement directly, you will get the answer of "no solution" if you encounter a ring.
We will think that if several points are connected into a strongly connected component, it is still based on the idea of greed. Of course, we walk through all the points in the strongly connected component. Why not take it if we can.
In that case, all strongly connected components are equivalent to points. The weight of this point is the sum of the weights of all points in the strongly connected component, as shown in the following figure.
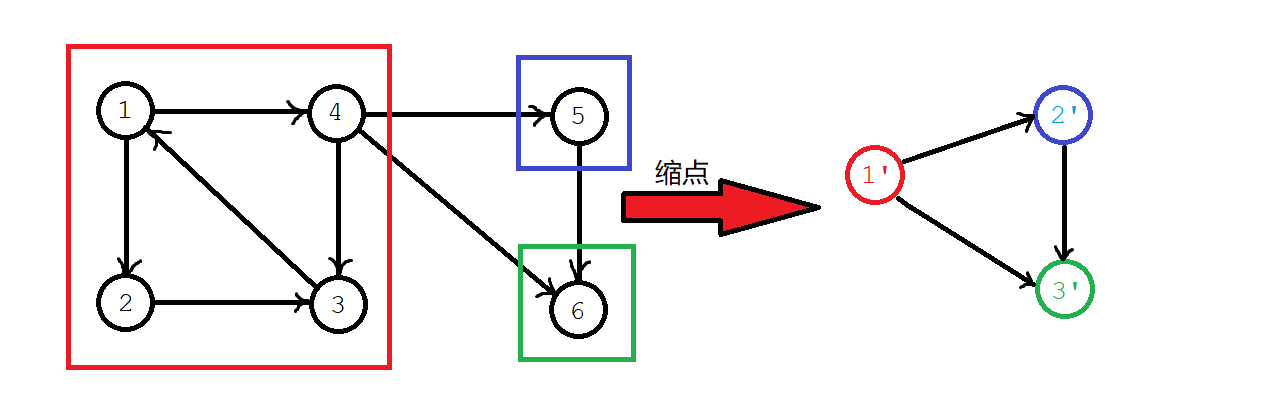
In this way, after finding all the strongly connected components and reducing them to points, we can get a DAG, and we can expand and arrange on it! QwQ
code
To tell you the truth, I really don't want to post this code. I feel refreshed when I write it. Finally, I finished the board question A on Luogu. However, because it is too messy, I really don't dare to optimize QwQ. Just make do with it.
/***After writing, even I dare not adjust the shrinking point QAQ***/
#include <cstdio>
#include <stack>
#include <queue>
using namespace std;
const int maxN = 2000001;
int top, n, m, cur, tot, ans;
int head[maxN], newhead[maxN];
int dfn[maxN], low[maxN];
int fa[maxN], color[maxN], index[maxN];
int dp[maxN], arr[maxN];
bool vis[maxN];
stack <int> stac;
queue <int> que;
struct Edge {
int to;
int next;
} edge[maxN], newedge[maxN];
inline void add_edge(int u, int v) {
edge[++top].to = v;
edge[top].next = head[u];
head[u] = top;
}
inline void add_new(int u, int v) {
newedge[++top].to = v;
newedge[top].next = newhead[u];
newhead[u] = top;
}
void tarjan(int u) { //Tarjan finding strongly connected components
dfn[u] = low[u] = ++cur;
vis[u] = true;
stac.push(u); //Each time a new node is searched, it is stacked
for(int ptr = head[u]; ptr; ptr = edge[ptr].next) {
int curv = edge[ptr].to;
if(!dfn[curv]) {
tarjan(curv);
low[u] = min(low[u], low[curv]); //Update low value through child node
}
else if(vis[curv]) { //If the found node is not in the stack, it means that the node is already in the strongly connected component, and there is no need to update the low value
low[u] = min(low[u], low[curv]);
}
}
if(dfn[u] == low[u]) { //dfn[u] == low[u] means that this point is a strongly connected component, divided into a "root" node
color[u] = ++tot; //dyeing
vis[u] = false; //Back stack operation
while(stac.top() != u) {
color[stac.top()] = tot;
vis[stac.top()] = false;
fa[stac.top()] = u;
stac.pop();
}
stac.pop();
}
}
void toposort(void) {
for(int i = 1; i <= n; ++i) {
if(index[fa[i]] == 0 && !vis[fa[i]]) {
vis[fa[i]] = true;
dp[fa[i]] = arr[i];
ans = max(dp[fa[i]], ans); //Update the ans value with a point with a penetration of 0
que.push(fa[i]); //Stack points with a degree of 0
}
}
while(!que.empty()) { //Topology sorting template
int curu = que.front();
que.pop();
for(int ptr = newhead[curu]; ptr; ptr = newedge[ptr].next) {
int curv = newedge[ptr].to;
--index[curv];
if(!index[curv]) {
que.push(curv);
}
dp[curv] = max(dp[curv], dp[curu] + arr[curv]); //The answer is updated each time the dp value of the node is updated.
ans = max(ans, dp[curv]);
}
}
}
int main(void) {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++i) {
scanf("%d", &arr[i]);
fa[i] = i;
}
for(int i = 1; i <= m; ++i) {
int ui, vi;
scanf("%d%d", &ui, &vi);
add_edge(ui, vi);
}
top = 0;
for(int i = 1; i <= n; ++i) {
if(!dfn[i]) { //A directed graph is not necessarily a strongly connected graph
tarjan(i);
}
}
for(int i = 1; i <= n; ++i) {
if(fa[i] != i) {
arr[fa[i]] += arr[i]; //Shrinking point
}
for(int ptr = head[i]; ptr; ptr = edge[ptr].next) { //Create new map
if(fa[edge[ptr].to] != fa[i]) {
add_new(fa[i], fa[edge[ptr].to]);
++index[fa[edge[ptr].to]];
}
}
}
toposort(); //Topological sorting
printf("%d", ans); //Output the maximum weight and
return 0;
}
//by CaO
Tarjan and LCA algorithm
LCA problem introduction
The so-called LCA is the Least Common Ancestors on the tree. The content of the problem is: given a rooted tree with \ (n \) nodes, the node number is \ (1,2,\cdots,n \)\ (m \) ask a pair of nodes numbered \ (a_i,b_i \) which point is the nearest common ancestor on the tree.
Tarjan algorithm for LCA
Tarjan algorithm can complete the offline algorithm of LCA within the complexity of \ (\ Theta(n) \) and \ (\ mathcal{O}(1) \) query. The algorithm process is as follows:
- Save all point pair numbers to be queried;
- Search the tree from the root node, and mark it as visited when searching a point; And merge all its child nodes with it during backtracking (you need to use union search set here);
- Traverse all nodes \ (V \) that have query relationship with the current node \ (u \). If \ (V \) has been accessed, the LCA of \ (u \) and \ (V \) is \ (\ textit{fa}[v] \).
As shown in the figure above, take this figure as an example and find \ (\ operatorname{LCA}(4,6) \) (for convenience, the operations accessed by the tag node are regarded as dyed green below):
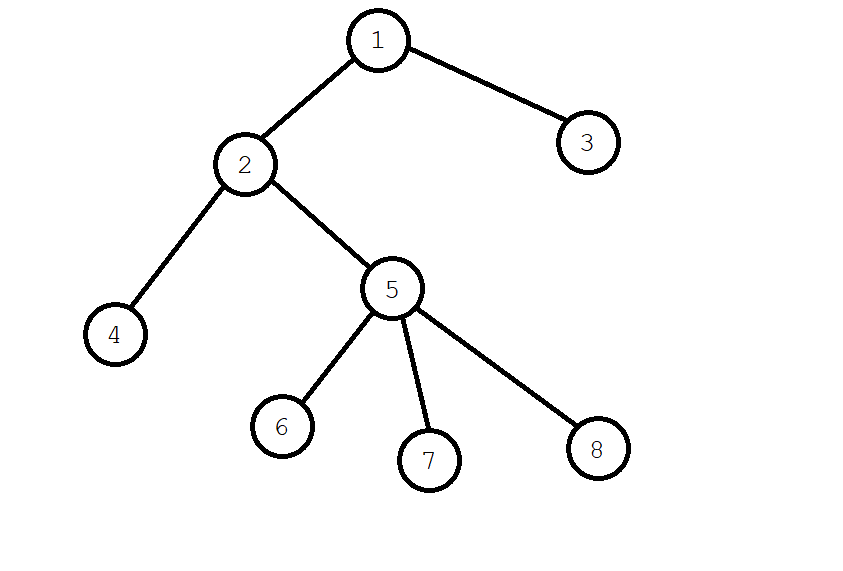
Start the search from node 1, dye node 1, and recursively search node \ (2 \).
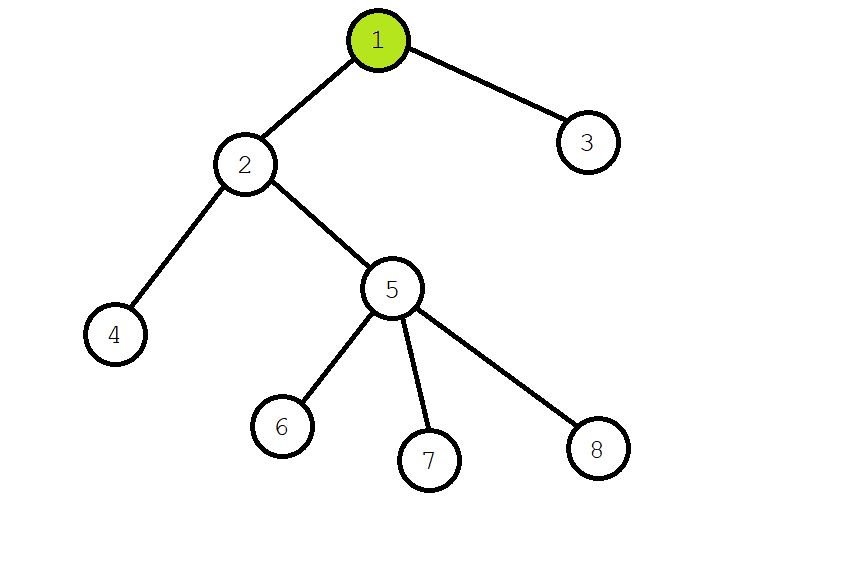
After node 2 is dyed green, traverse its subtree and meet node 4. The query relationship with node 4 is \ (6 \), but it has not been queried, regardless of it.
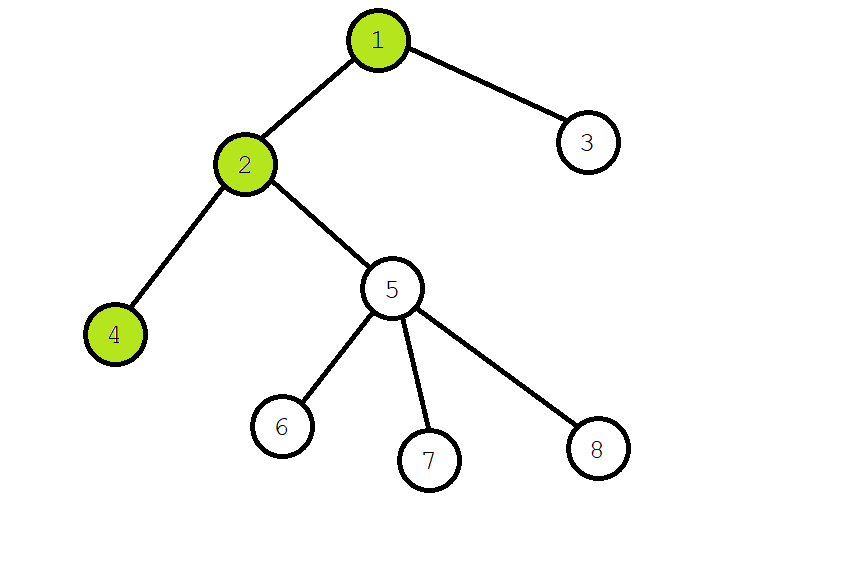
When tracing back, merge node 4 and node 2.
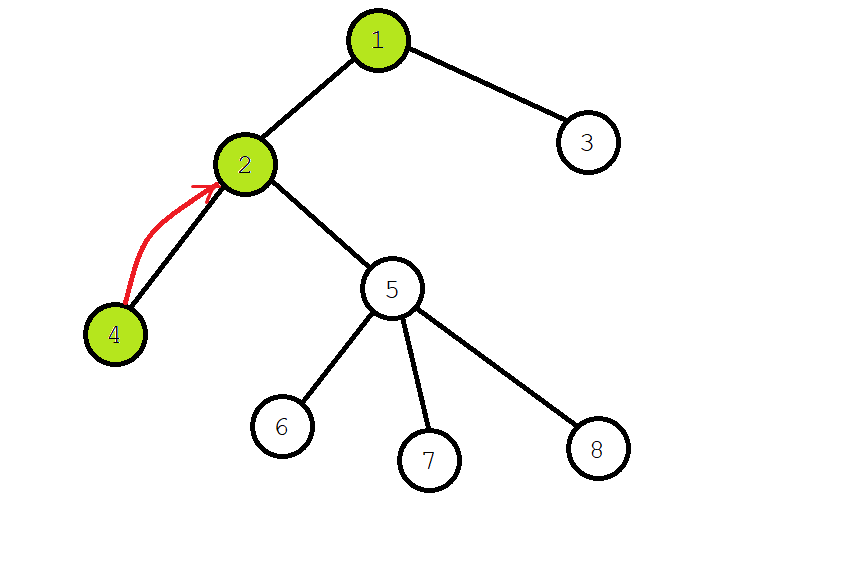
Search another subtree of \ (2 \), dye \ (5 \), recursively find the node of \ (6 \), and dye \ (6 \).
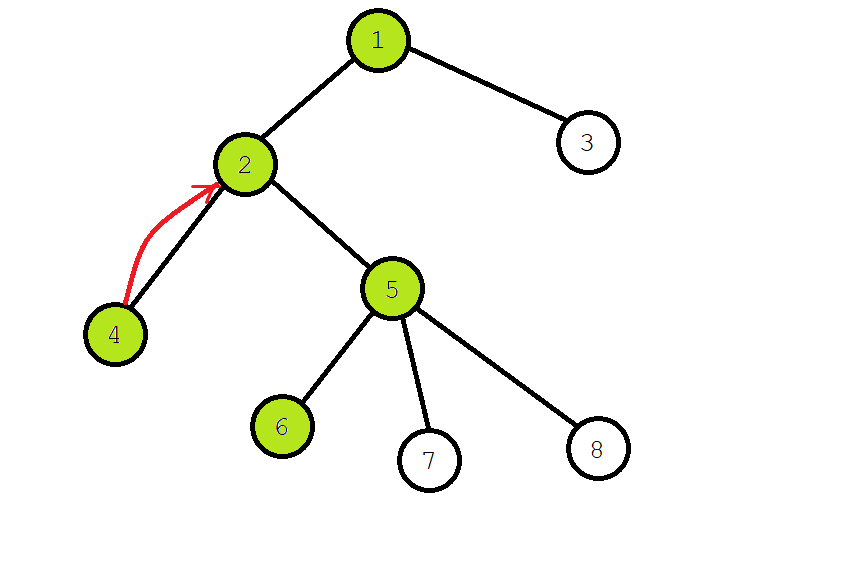
We found that \ (6 \) has a query relationship with \ (4 \), and \ (4 \) has been accessed, so we can know \ (\ operatorname{LCA}(6,4)=\textit{fa}[4]=2 \).
An algorithm like this can find the LCA of any two nodes in one DFS, which is more efficient than multiplication. You can try to simulate it with your own pen.
code
#include <cstdio>
using namespace std;
const int maxN = 200001;
int head[maxN], query[maxN], fa[maxN];
int n, m, top;
bool isRoot[maxN], vis[maxN], answered[maxN];
struct Edge {
int to;
int next;
int num;
} edge[maxN], ans[maxN]; //edge records the original tree, and answer records all the point pairs to be queried
inline void add_edge(int u, int v) {
edge[++top].to = v;
edge[top].next = head[u];
head[u] = top;
}
inline void add_query(int u, int v, int num) { //Add query team
ans[++top].to = v;
ans[top].next = query[u];
ans[top].num = num;
query[u] = top;
}
//Query set template
inline void init(int n) {
for(int i = 1; i <= n; ++i) {
fa[i] = i;
isRoot[i] = true;
}
}
int find(int x) {
if(fa[x] == x) {
return x;
}
else {
fa[x]=find(fa[x]);
return fa[x];
}
}
inline void merge(int x, int y) {
fa[find(x)] = find(y); //Notice that the direction of the merge is x and y
}
void tarjan(int x) {
vis[x] = true; //Mark that the point has been accessed
for(int ptr = head[x]; ptr; ptr = edge[ptr].next) {
int curv = edge[ptr].to;
tarjan(curv);
merge(curv, x); //Merge child nodes
}
for(int ptr = query[x]; ptr; ptr = ans[ptr].next) {
int curv = ans[ptr].to, num = ans[ptr].num;
if(vis[curv] && !answered[num]) {
printf("LCA(%d, %d) = %d\n", x, curv, find(curv)); //Output answers offline
answered[num] = true; //You don't have to answer the same question twice
}
}
}
int main(void) {
scanf("%d%d", &n, &m);
init(n);
for(int i = 1; i < n; ++i) {
int ui, vi;
scanf("%d%d", &ui, &vi);
add_edge(ui, vi);
isRoot[vi] = false;
}
top = 0;
for(int i = 1; i <= m; ++i) {
int ui, vi;
scanf("%d%d", &ui, &vi);
add_query(ui, vi, i);
add_query(vi, ui, i);
}
for(int i = 1; i <= n; ++i) {
if(isRoot[i]) { //DFS from root node
tarjan(i);
}
}
return 0;
}
//by CaO
Examples
This list of topics will be continuously updated.
- Luogu P3379 [template] nearest common ancestor (LCA)
This question is the template question of LCA, but it can't be AC with the above code. It can be doubled or Tarjan. - Luogu P3387 [template] shrinking point
The simplest application of shrinking point + expanding dp is that the code is really dizzy( - Luogu P2341 [USACO03FALL][HAOI2006] popular cattle G
The simple application of shrinking points is still the idea of expanding and arranging after shrinking points. You can try to do it. - Luogu P2863 [USACO06JAN]The Cow Prom S
This problem is very basic to find the strongly connected component, but pay attention to output points greater than \ (1 \).