1. Recursion

1. Find duplicate

   • Find a way to divide
   • Find recursive formula or equivalent transformation

2. Find change

   The variable is usually used as a parameter

3. Find boundary

Simple basic questions (practice three steps)

• Find the factorial of n

  public class demo01 {
  	public static void main(String[] args) {
  		int a = f1(4);
  		System.out.println(a);
  	}
  	
  	// Calculate factorial value
  	public static int f1(int n) {
  		if(n == 1)
  			return 1;
  		return n*f1(n-1);
  	}
  }
  

• Print i to j

  public class demo02 {
  	public static void main(String[] args) {
  		f2(4,8);
  	}
  
  	// Print out i to j
  	public static void f2(int i, int j) {
  		if(i > j)
  			return;
  		System.out.print(i+" ");
  		f2(i+1,j);
  	}
  }
  

• Sum all elements of arr

  public class demo03 {
  	public static void main(String[] args) {
  		int[] arr = new int[]{1, 2, 3, 4, 5};
  		int res = f3(arr, 0);
  		System.out.println(res);
  	}
  	
  	// Sum all elements of arr
  	public static int f3(int[] arr, int begin) {
  		if(begin == arr.length-1)
  			return arr[begin];
  		return arr[begin] + f3(arr, begin+1);
  	}
  }
  

• Flip string

  public class demo04 {
  	public static void main(String[] args) {
  		String s = "a54s5d";
  		System.out.println(f4(s, s.length()-1));
  	}
  
  	// Flip string
  	public static String f4(String s, int end) {
  		if (end == 0) {
  			return "" + s.charAt(0);
  		}
  		return s.charAt(end)+f4(s, end-1);
  	}
  }
  

Basic questions (change in repetition, repetition in change)

Recursion:

The above example is the direct quantity + small gauge mold problem

The following examples are multiple small gauge mold problems

● Fibonacci series

Find the recurrence formula f(n) = f(n-1) + f(n-2)

public class demo05 {
    // test
	public static void main(String[] args) {
		System.out.println(fib(3));
	}
	
    // Fibonacci sequence 
	public static int fib(int n) {
		if(n == 1 || n == 2)
			return 1;
		return fib(n-1) + fib(n-2);	// Recursive tree, when n is large, the scale is large
	}
}

● maximum common divisor

Rolling division method m% n = k

If k = 0, then n is the greatest common divisor

If K ≠ 0, then n% k = k ` (repeat this until the remainder is 0)

public class demo03 {
    // test
	public static void main(String[] args) {
		System.out.println(gcd(15, 9));
	}
	
    // greatest common divisor  
	public static int gcd(int m, int n) {
		if (n == 0) {
			return m;
		}
		return gcd(n, m % n);
	}
}

● insert sort recursively

Insert sort is to treat the array as an ordered table and an unordered table. One number is taken out of the unordered table each time and sorted in the ordered table.

public class demo04 {
	public static void main(String[] args) {
		int[] arr = new int[]{5,8,3,4,1};
		insertSort(arr, arr.length-1);
		for (int i : arr) {
			System.out.print(i+" ");
		}
	}
	
	public static void insertSort(int[] arr, int k) {
		if(k == 0)
			return;
		
		// Sort the first k-1 elements
		insertSort(arr, k-1);
		
		// Insert the element of position k into the previous part
		int x = arr[k];
		int index = k - 1;
		while(index > -1 && x < arr[index]) {
			arr[index+1] = arr[index--];
		}
		arr[index+1] = x;
	}
}

● tower of Hanoi 🔺

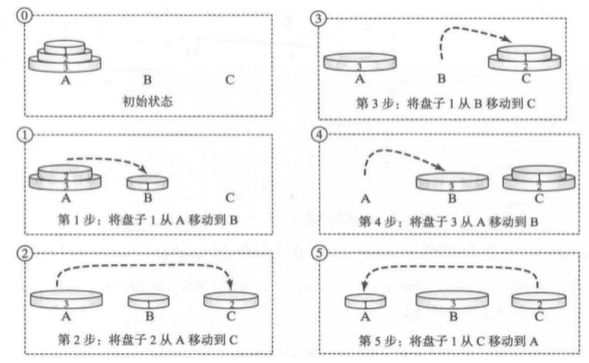
1 ~ N move from A to B, C as auxiliary

Equivalent to:

• Move 1 ~ N-1 from A to C and B as auxiliary
• Move N from A to B
• Move 1 ~ N-1 from C to B, A as auxiliary

// Hanoi Tower recursive solution

public class demo05 {
	public static void main(String[] args) {
		HanoiTower(3, "A", "B", "C");
	}
	
  /**
   * Print the path of moving N plates from source to target
   * @param N       The initial n plates arrive from childhood, and N is the maximum number
   * @param from 	Original column
   * @param to 		Target column
   * @param help    Auxiliary column
   */
	public static void HanoiTower(int N, String from, String to, String help){
		if(N == 1) {
			System.out.println("move " + N + " from " + from + " to " + to);
			return;
		}
		
		// Move 1 ~ N-1 to the auxiliary column
		HanoiTower(N - 1, from, help, to);
		// N successfully reached target
		System.out.println("move " + N + " from " + from + " to " + to);
		// Move 1 ~ N-1 from the auxiliary column to the target column
		HanoiTower(N - 1, help, to, from);
	}
}

2. Find

Binary search

public class binarySearch {
	public static int BinarySearch(int[] arr, int low, int high, int target) {
		if(low > high)
			return -1;
		int mid = low + ((high- low) >> 1);
//		int mid = (low + high) >>> 1; 	 Prevent overflow and shift efficiently
		if(arr[mid] > target)
			return BinarySearch(arr, low, mid-1, target);
		else if(arr[mid] < target)
			return BinarySearch(arr, mid+1, high, target);
		else 
			return mid;
	}
	
	// test
	public static void main(String[] args) {
		int[] arr = new int[] {1,5,8,10,13,21,55};
		System.out.println(BinarySearch(arr, 0, arr.length-1, 13));
	}
}

3. Sorting

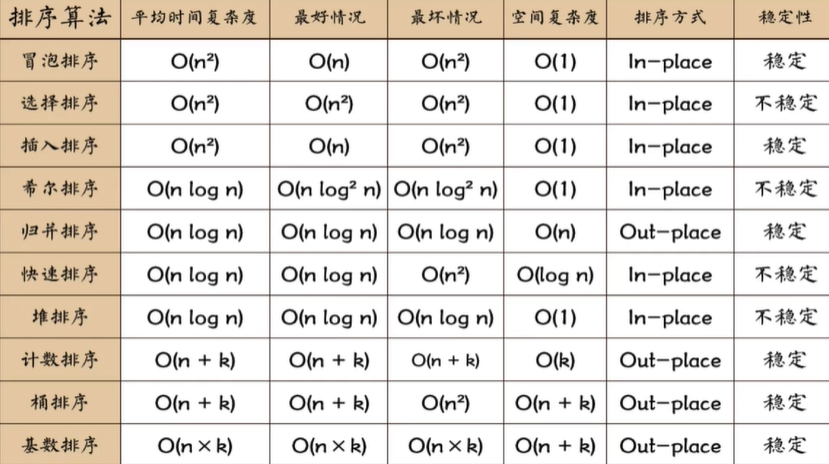
Bubble sorting

• Time complexity: O(n) ²)

• Space complexity: O(1)
• Stability: the relative position of the same element will not change before and after sorting, that is, it is stable

import java.util.Arrays;

public class bubbleSort {
	public static void BubbleSort1(int[] arr) {
        if (arr == null || arr.length <= 1) {
			return;
		}
        
		for(int i = 0; i < arr.length - 1; i++) {	// Number of cycles, i.e. bubbling in the i-th cycle
			for(int j = 0; j < arr.length - 1 - i; j++) {	// Pairwise comparison sort
				if(arr[j] > arr[j + 1]) {
					int temp = arr[j];
					arr[j] = arr[j + 1];
					arr[j + 1] = temp;
				}
			}
		}
	}
	
	// improvement
	public static void BubbleSort2(int[] arr) {
		for(int i = 0; i < arr.length - 1; i++) {
			// Mark whether there is exchange on this trip. If there is no exchange, the order has been arranged
			// At the beginning of each round, it is assumed that the order has been arranged
			boolean flag = true;
			for(int j = 0; j < arr.length - 1 - i; j++) {
				if(arr[j] > arr[j + 1]) {
					int temp = arr[j];
					arr[j] = arr[j + 1];
					arr[j + 1] = temp;
					flag = false;	// An exchange indicates that this round is not in order
				}
			}
			
			// If there is no exchange, the order is already arranged, and there is no need to carry out the next round of bubbling
			if(flag) {
				break;
			}
		}
	}
	
	// test
	public static void main(String[] args) {
		int[] array1 = new int[]{55, 33, 22, 66, 11};
        System.out.print("Before sorting:");
        System.out.println(Arrays.toString(array1));
        
        // Call the BubbleSort1 method to sort the array
        BubbleSort1(array1);
        System.out.print("BubbleSort1 After sorting:");
        System.out.println(Arrays.toString(array1));
        
        // Call the improved BubbleSort2 method to sort the array
        int[] array2 = new int[]{55, 33, 22, 66, 11};
        BubbleSort2(array2);
        System.out.print("BubbleSort2 After sorting:");
        System.out.println(Arrays.toString(array2));
        
        // Array.sort()
        int[] array3 = new int[]{55, 33, 22, 66, 11};
        Arrays.sort(array3);
        System.out.print("Arrays.sort After sorting:");
        System.out.println(Arrays.toString(array3));
        
        // You can use long now = system currentTimeMillis();
	}
}

 

Select sort

• Time complexity: O(n) ²)
• Space complexity: O(1)
• Stability: unstable

import java.util.Arrays;

public class selectionSort {
	// Select sort
	public static void SelectionSort(int[] arr) {
        if (arr == null || arr.length <= 1) {
			return;
		}
        
		// Select the smallest (or largest) element from the data elements to be sorted in each trip as the first element until all elements are arranged
		for(int i = 0; i < arr.length - 1; i++) {	
			int min = i;	
			for(int j = i + 1; j < arr.length; j++) {
				if(arr[min] > arr[j])
					min = j;
			}
			if(min != i)
				swap(arr, i, min);
		}
	}
	
	// exchange
	public static void swap(int[] arr, int a, int b) {
		int temp = arr[a];
		arr[a] = arr[b];
		arr[b] = temp;
	}
	
	// test
	public static void main(String[] args) {
		int[] arr = {4, 5, 6, 3, 2, 1};
		System.out.print("Before sorting:");
        System.out.println(Arrays.toString(arr));
		SelectionSort(arr);
		System.out.print("SelectionSort After sorting:");
		System.out.println(Arrays.toString(arr));

		int[] arr2 = {4, 5, 6, 3, 2, 1};
		Arrays.sort(arr2);
        System.out.print("Arrays.sort After sorting:");
        System.out.println(Arrays.toString(arr2));
	}
}

 

Insert sort

• Time complexity: O(n) ²)
• Space complexity: O(1)
• Stability: stable

import java.util.Arrays;

public class insertSort {
	// Insert sort
	public static void InsertSort(int[] arr) {
		if (arr == null || arr.length <= 1) {
			return;
		}
		
		for(int i = 1; i < arr.length; i++) {	// The first element is ordered, starting with the second
			int temp = arr[i];	// Number of to insert
			int j = i - 1;		// Scan the sorted part forward for insertion
			while(j >= 0 && arr[j] > temp) {
				arr[j + 1] = arr[j];	// temp is smaller than arr[j]. Move arr[j] backward
				j--;
			}
			arr[j + 1] = temp;
		}
	}
	
	// test
	public static void main(String[] args){
        int[] arr = {51,2,35,64,55,14,34,28,9};
        
        System.out.print("Before sorting:");
        System.out.println(Arrays.toString(arr));
        InsertSort(arr);
		System.out.print("SelectionSort After sorting:");
		System.out.println(Arrays.toString(arr));

		int[] arr2 = {51,2,35,64,55,14,34,28,9};
		Arrays.sort(arr2);
        System.out.print("Arrays.sort After sorting:");
        System.out.println(Arrays.toString(arr2));
    }
}

 

Shell Sort

• Time complexity: in O (nlogn) ～ o (n) ²) between
• Space complexity: O(1)
• Stability: unstable

import java.util.Arrays;

public class shellSort {
	// Shell Sort 
	public static void ShellSort(int[] arr) {
		if(arr == null || arr.length <= 1)
			return;
		
		// Change of control increment of outer loop
		for(int interval = arr.length/2; interval > 0; interval/=2) {
			// The inner loop performs insertion sorting with an increment of interval
			for(int i = interval; i < arr.length; i++) {
				int temp = arr[i];
				int idx = i - interval;
				while(idx >= 0 && arr[idx] > temp) {
					arr[idx + interval] = arr[idx];
					idx -= interval;
				}
				arr[idx + interval] = temp;
			}
		}
	}
	
	// test
	public static void main(String[] args){
        int[] arr = {51,2,35,64,55,14,34,28,9};
        
        System.out.print("Before sorting:");
        System.out.println(Arrays.toString(arr));
        ShellSort(arr);
		System.out.print("SelectionSort After sorting:");
		System.out.println(Arrays.toString(arr));

		int[] arr2 = {51,2,35,64,55,14,34,28,9};
		Arrays.sort(arr2);
        System.out.print("Arrays.sort After sorting:");
        System.out.println(Arrays.toString(arr2));
    }
}

 

Quick sort (divide and conquer)

Fast platoon - > Division

Array. In jdk Sorts () is a fast scheduling algorithm used

● one pass unidirectional scanning method

Idea:

Array with two pointers:

• Scan_pos - sp, from left to right, confirm that the value is less than or equal to the principal element;
• The matrix on the right - rp, from the right interval to the left, confirms the elements whose value is greater than the principal element;

It is divided into three sections:

• The interval swept by sp is the interval less than or equal to the principal element;
• The interval swept by rp is the interval larger than the principal component;
• The interval between sp and rp is not unknown.

import java.util.Arrays;

public class quickSort {
	public static void QuickSort1(int[] arr, int l, int r) {
		if(l < r) {
			int q = Partition(arr, l, r);
			QuickSort1(arr, l, q - 1);
			QuickSort1(arr, q + 1, r);
		}
	}

	public static int Partition(int[] arr, int p, int r) {
		int pivot = arr[p];
		int sp = p + 1;		// Scan pointer
		int rp = r;			// Right hand pointer
		while(sp <= rp) {
			if(arr[sp] <= pivot)
				sp++;
			else {
				swap(arr, sp, rp);
				rp--;
			}
		}
		swap(arr, p, rp);
		return rp;
	}

	public static void swap(int[] arr, int a, int b) {
		int temp = arr[a];
		arr[a] = arr[b];
		arr[b] = temp;
	}
    
    // test
	public static void main(String[] args){
        int[] arr = {51,2,35,64,55,14,34,28,9};
        
        System.out.print("Before sorting:");
        System.out.println(Arrays.toString(arr));
		System.out.print("QuickSort1 After sorting by one-way scanning method:");
        QuickSort1(arr, 0, 8);
		System.out.println(Arrays.toString(arr));

		int[] arr2 = {51,2,35,64,55,14,34,28,9};
		Arrays.sort(arr2);
        System.out.print("Arrays.sort After sorting:");
        System.out.println(Arrays.toString(arr2));
    }
}

● bidirectional scanning zoning method

Idea:

Scan the head and tail pointer to the middle, find the elements larger than the principal element from the left, find the elements less than or equal to the principal element from the right, exchange them, and continue scanning until there are no large elements on the left and small elements on the right.

Modify the Partition:

public static int Partition2(int[] arr, int p, int r) {
    // Optimization, choose an intermediate value between P, R and mid as the principal component
    int mid = p + ((r - p) >> 1);	// Subscript in the middle of the array
    int midValIdx = -1;				// Of the three is the subscript of the median
    if((arr[p] >= arr[mid] && arr[p] <= arr[r]) || (arr[p] <= arr[mid] && arr[p] >= arr[r]))
        midValIdx = p;
    else if((arr[r] >= arr[mid] && arr[r] <= arr[p]) || (arr[r] <= arr[mid] && arr[r] >= arr[p]))
        midValIdx = r;
    else 
        midValIdx = mid;
    swap(arr, p, midValIdx);

    int pivot = arr[p];
    int lp = p + 1;		// Left hand pointer
    int rp = r;			// right
    while (lp <= rp) {
        while (lp <= rp && arr[lp] <= pivot) lp++;
        while (lp <= rp && arr[rp] > pivot) rp--;
        if(lp < rp)
            swap(arr, lp, rp);
    }
    swap(arr, p, rp);
    return rp;
}

● three pointer zoning method

Available when there are many repetitions in the primary element

Idea:

On the basis of unidirectional scanning, a pointer ep is added to point to the area with equal principal elements.

After ep points to the first element equal to pivot, sp points to the element:

• Less than the principal element, sp exchanges with ep, ep + +, sp + +;
• Equal to the principal element, sp + +;
• If it is larger than the principal element, sp exchanges with rp, rp –.

 

Merge sort (divide and conquer)

Merge - > merge

Idea: divide the array into left and right sub arrays, recursively call merge to sort, and then use the auxiliary merge function to merge the two ordered sub arrays into an overall ordered array

• Time complexity: O (nlogn)
• Space complexity: it is necessary to open up an auxiliary space, which can be reused. The size is array length N
• Stability: stable

import java.util.Arrays;

public class mergeSort {
	private static int[] helper;
	
	public static void MergeSort(int[] arr) {
		// Open up auxiliary space
		helper = new int[arr.length];
		MergeSort(arr, 0, arr.length - 1);
	}
	
	public static void MergeSort(int[] arr, int p, int r) {
		if(p < r) {
			int mid = p + ((r - p) >> 1);	
			MergeSort(arr, p, mid);			// Sort left
			MergeSort(arr, mid + 1, r);		// Sort right
			merge(arr, p, mid, r);	// merge
		}
	}
	/**
	 * @param arr Original array
	 * @param p   Low position
	 * @param mid Median
	 * @param r   high position
	 */
	public static void merge(int[] arr, int p, int mid, int r) {
		// Copy the original array to the corresponding position in the helper
		System.arraycopy(arr, p, helper, p, r-p+1);
		// Three pointers
		int left = p, right = mid + 1;
		int current = p;
		// Compare merge
		while(left <= mid && right <= r) {
			if(helper[left] <= helper[right]) {
				arr[current++] = helper[left++];
			}else {
				arr[current++] = helper[right++];
			}
		}
		
		// If the left row is finished and there are still items on the right that have not been compared, they need not be processed (they have been placed in the corresponding position in the arr)
		// If the row on the right side is finished and there are still items not compared on the left side, move the remaining items on the left side to the arr
		while(left <= mid) {
			arr[current++] = helper[left++];
		}
	}
	
	// test
	public static void main(String[] args){
        int[] arr = {51,2,35,64,55,14,34,28,9};
        
        System.out.print("Before sorting:");
        System.out.println(Arrays.toString(arr));
		System.out.print("MergeSort After sorting:");
		MergeSort(arr);
		System.out.println(Arrays.toString(arr));

		int[] arr2 = {51,2,35,64,55,14,34,28,9};
		Arrays.sort(arr2);
        System.out.print("Arrays.sort After sorting:");
        System.out.println(Arrays.toString(arr2));
    }
}

 

Heap sort

• Binary reactor

  • The key value of the parent node is always ≥ (≤) the key value of any child node
  • The left and right subtrees of each node are a binary heap (both the maximum heap or the minimum heap).

• The value of any node is greater than the value of its child node - large top heap

  The value of any node is less than the value of its child node - small top heap

• Heap sort

  1. Heap, reverse adjustment so that each sub number is a large top heap or a small top heap

     Start from n/2-1 elements to repair downward, and repair each node into a small (large) top heap

  2. Output elements in sequence: swap the top and the last elements, then adjust the top elements.

     The small top heap can sort the array in reverse order. Each time the top and end elements of the stack are exchanged, the top of the stack is repaired downward, so that the small elements reach the top of the heap again

• Small top pile

// Heap
public static void makeMinHeap(int[] arr) {	// Small top pile
    int n = arr.length;
    for(int i = n/2-1; i >= 0; i--) {
        minHeapFixDown(arr, i, n);
    }
}
// Generate small top pile
public static void minHeapFixDown(int[] arr, int i, int n) {
    // Left and right children of node i
    int left = 2 * i + 1;
    int right = 2 * i + 2;
    // Judge whether the boundary is crossed
    if(left >= n)	return;	// The left child crosses the boundary, that is, there is no left child, and i is the leaf node
    int min = left;		
    if(right >= n) {	// If the right child crosses the boundary, there is no right child
        min = left;
    }else {		// If both left and right children exist
        if(arr[left] > arr[right])
            min = right;
    }
    // min points to the younger of the left and right children

    // Judge the size relationship between i node and left and right child nodes
    if(arr[i] <= arr[min])	return;	 // If i is less than children, no exchange is made
    // If i is greater than children, exchange with younger children
    swap(arr,i,min);
    // Check and adjust the small top heap of the exchanged child nodes
    minHeapFixDown(arr, min, n);
}

public static void sort(int[] arr) {
    // Heap
    makeMinHeap(arr);
    // sort
    for(int x = arr.length - 1; x >= 0; x--) {
        // Swap the top of the heap (element 0) with the last element
        swap(arr, 0, x);
        // Reduce the scope of the heap (- 1 each time) and make the minimum heap adjustment for the elements at the top of the heap
        minHeapFixDown(arr, 0, x);
    }
}

• Large top pile

// Large top pile
public static void makeMaxHeap(int[] arr) {
    int n = arr.length;
    for(int i = n/2-1; i >= 0; i--) {
        MaxHeapFixDown(arr, i, n);
    }
}
public static void MaxHeapFixDown(int[] arr, int i, int n) {
    // Left and right children
    int left = i * 2 + 1;
    int right = i * 2 + 2;

    // Is it out of bounds
    if(left >= n) return;
    int max = left;
    if(right >= n) {
        max = left;
    }else {
        if(arr[left] < arr[right])
            max = right;
    }
    // max points to the older of the left and right children

    // i node and child node to judge
    if(arr[i] >= arr[max])	return;
    swap(arr, i, max);
    // Check and adjust the exchanged nodes
    MaxHeapFixDown(arr, max, n);
}
public static void sort2(int[] arr) {
    // Heap
    makeMaxHeap(arr);
    // sort
    for(int x = arr.length-1; x >= 0; x--) {
        swap(arr, 0, x);
        MaxHeapFixDown(arr, 0, x);
    }
}

For testing:

public static void main(String[] args) {
    int[] arr = {36,6,34,11,81,18,61,47,99,7};

    System.out.print("Before sorting:");
    System.out.println(Arrays.toString(arr));
    System.out.print("After heap sorting(Reverse order): ");
    sort1(arr);
    System.out.println(Arrays.toString(arr));
    System.out.print("After heap sorting(positive sequence): ");
    sort2(arr);
    System.out.println(Arrays.toString(arr));
}

 

Count sort

Idea:

Open up a new space with the size of max(source), scan the source, take value as the subscript of the auxiliary space, and record the number of value with the change position element of the auxiliary space.

After that, you can repair the source to be arranged in ascending order by traversing the helper:

• If the value of this bit (index) is 0, it means that index has not appeared in source;

• If the value of this bit (index) is 1, it means that the index appears once in the source. If it is 2, it naturally appears twice.

Time complexity: scan the source once and the helper once, and the complexity is N+k;

Space complexity: auxiliary space K, k=maxOf(source).

Existing problems:

1. Repeating element

   // Count sort (the original array has duplicate values)
   public static void sort(int[] source) {
       int[] helper = new int[maxOf(source) + 1];
       for(int e : source) {
           helper[e]++;
       }
   
       int current = 0; //Location of data backfill
       for(int i = 0; i < helper.length; i++) {
           while(helper[i] > 0) {
               source[current++] = i;
               helper[i]--;
           }
       }
   }
   

2. Negative number

   Find out the max value and min value of the original array. The space size of the auxiliary array is max min + 1, with source[i]-min as the subscript.

   // Count sort (the original array has a negative number)
   public static void CountSort(int[] source) {
       int min = minOf(source);
       int max = maxOf(source);
       int[] helper = new int[max - min + 1];
       for(int e : source) {
           helper[e - min]++;
       }
   
       int current = 0;
       for(int i = 0; i < helper.length; i++) {
           while (helper[i] > 0) {
               source[current++] = i + min;
               helper[i]--;
           }
       }
   }
   

Test:

// Array maximum
public static int maxOf(int[] arr) {
    int max = 0;
    for(int i = 1; i < arr.length; i++) {
        if(arr[i] > arr[max])
            max = i;
    }
    return arr[max];
}
// Array minimum
public static int minOf(int[] arr) {
    int min = 0;
    for(int i = 1; i < arr.length; i++) {
        if(arr[i] < arr[min])
            min = i;
    }
    return arr[min];
}
// test
public static void main(String[] args){
    int[] arr = {51,2,2,55,2,14,34,28,9};

    System.out.print("Before sorting:");
    System.out.println(Arrays.toString(arr));
    System.out.print("After counting and sorting(Array value is repeatable,Cannot be negative): ");
    sort(arr);
    System.out.println(Arrays.toString(arr));

    System.out.println("=====================");

    int[] arr2 = {51,2,2,55,2,14,34,28,-9};
    System.out.print("Before sorting:");
    System.out.println(Arrays.toString(arr2));
    System.out.print("After counting and sorting(Array value is repeatable,Can also be negative): ");
    CountSort(arr2);
    System.out.println(Arrays.toString(arr2));
}

 

Bucket sorting

• Assign & collect
• Idea: Design K buckets (No. 0 ~ k-1), then distribute n input numbers to each bucket, sort the numbers in each bucket, and then list the elements in each bucket in order.

 

Cardinality sort

• Assign & collect
• Idea: for decimal numbers, the number of each bit is in [0,9], and the number of d bits has column D. Cardinality sorting: sort according to the lower significant digits, and then sort up one by one until the end of the highest ranking sorting.
• Question: there is no 0 or negative number in the number to be arranged

import java.util.ArrayList;
import java.util.Arrays;

public class radixSort {
	// Generate 10 buckets, and the number of each bucket is variable: use array + ArrayList
	private static ArrayList[] bucket = new ArrayList[10];
	
	// Initialization bucket (static block initialization bucket, which is executed when the class is generated)
	static {
		for(int i = 0; i < bucket.length; i++) {
			bucket[i] = new ArrayList();
		}
	}
	
	// For each round of sorting, arr is the original array and d is the number of bits
	public static void sort(int[] arr, int d) {
		// Barrel in
		for(int i = 0; i < arr.length; i++) {
			putInBucket(arr[i], getDigitOn(arr[i], d));
		}
		
		// Barrel out
		int current = 0;
		for(int j = 0; j < bucket.length; j++) {
			for(Object o : bucket[j]) {
				arr[current++] = (Integer) o;
			}
		}
		
		// Empty bucket
		clearAll();
	}
	
	// Barrel in
	public static void putInBucket(int data, int digitOn) {
		switch (digitOn) {
		case 0:
			bucket[0].add(data);
			break;
		case 1:
			bucket[1].add(data);
			break;
		case 2:
			bucket[2].add(data);
			break;
		case 3:
			bucket[3].add(data);
			break;
		case 4:
			bucket[4].add(data);
			break;
		case 5:
			bucket[5].add(data);
			break;
		case 6:
			bucket[6].add(data);
			break;
		case 7:
			bucket[7].add(data);
			break;
		case 8:
			bucket[8].add(data);
			break;
		default:
			bucket[9].add(data);
			break;
		}
	}
	
	// empty
	public static void clearAll() {
		for(ArrayList b : bucket) {
			b.clear();
		}
	}
	
	// sort
	public static void radixSort(int[] arr) {
		int d = 1;	// The bit into the bucket is initialized to 1, that is, the lowest bit
		int max = maxOf(arr);	// Array maximum
		
		// Number of digits of maximum value
		int dNum = 1;
		while(max / 10 != 0) {
			dNum++;
			max /= 10;
		}
		
		// Enter and exit the barrel according to the digit cycle
		while (d <= dNum) {
			sort(arr, d++);
		}
	}
	
	// Array maximum
	public static int maxOf(int[] arr) {
		int max = 0;
		for(int i = 1; i < arr.length; i++) {
			if(arr[i] > arr[max])
				max = i;
		}
		return arr[max];
	}
	
	// The i-th digit of a number (from the lower digit)
	public static int getDigitOn(int x, int i) {
		int e = 0;
		while(i >= 1) {
			e = x % 10;
			x /= 10;
			i--;
		}
		return e;
	}
	
	// test
	public static void main(String[] args){
        int[] arr = {51,2,2,55,2,14,34,28,9};
        
        System.out.print("Before sorting:");
        System.out.println(Arrays.toString(arr));
		System.out.print("Cardinality sorting:");
		radixSort(arr);
		System.out.println(Arrays.toString(arr));

    }
}