Algorithm series (II) parallel search set
preface
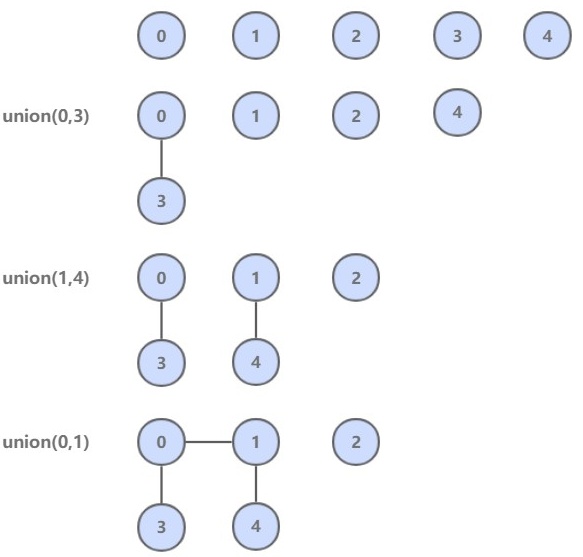
It is used to solve the problem of dynamic connectivity. It can dynamically connect two points and judge whether the two points are connected.
| method | describe |
|---|---|
| UF(int N) | Construct a union search set with size N |
| void union(int p, int q) | Connecting p and q nodes |
| int find(int p) | Find the connected component number where p is located |
| boolean connected(int p, int q) | Judge whether the p and q nodes are connected |
public abstract class UF {
protected int[] id;
public UF(int N) {
id = new int[N];
for (int i = 0; i < N; i++) {
id[i] = i;
}
}
public boolean connected(int p, int q) {
return find(p) == find(q);
}
public abstract int find(int p);
public abstract void union(int p, int q);
}
Quick Find
You can quickly find, that is, you can quickly judge whether the two nodes are connected.
To ensure that the id values of all nodes of the same connected component are equal, we can judge whether the id values of two nodes are equal, so as to judge their connectivity.
However, the cost of union operation is very high. It is necessary to modify the id values of all nodes in one connected component to the id values of another node.
public class QuickFindUF extends UF {
public QuickFindUF(int N) {
super(N);
}
@Override
public int find(int p) {
return id[p];
}
@Override
public void union(int p, int q) {
int pID = find(p);
int qID = find(q);
if (pID == qID) {
return;
}
for (int i = 0; i < id.length; i++) {
if (id[i] == pID) {
id[i] = qID;
}
}
}
}
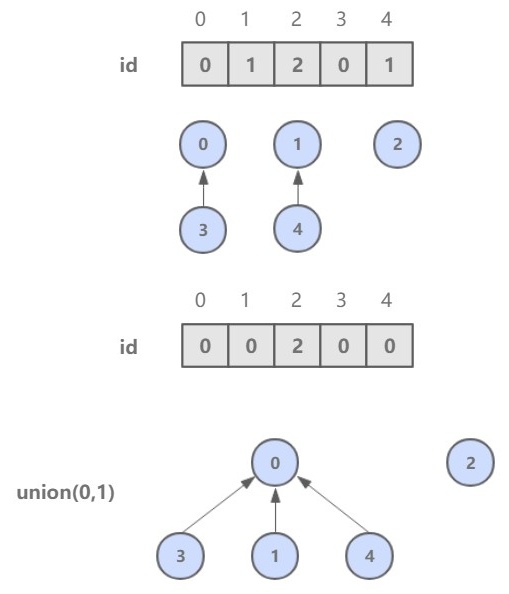
Quick Union
The union operation can be carried out quickly. You only need to modify the id value of a node.
However, the find operation costs a lot, because the node id values of the same connected component are different, and the id value is only used to point to another node. Therefore, you need to look up until you find the top node.
public class QuickUnionUF extends UF {
public QuickUnionUF(int N) {
super(N);
}
@Override
public int find(int p) {
while (p != id[p]) {
p = id[p];
}
return p;
}
@Override
public void union(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot != qRoot) {
id[pRoot] = qRoot;
}
}
}
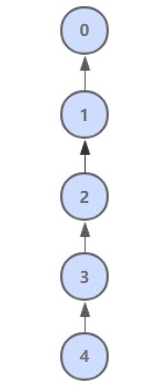
This method can perform union operation quickly, but the find operation is directly proportional to the tree height. In the worst case, the height of the tree is the number of nodes.
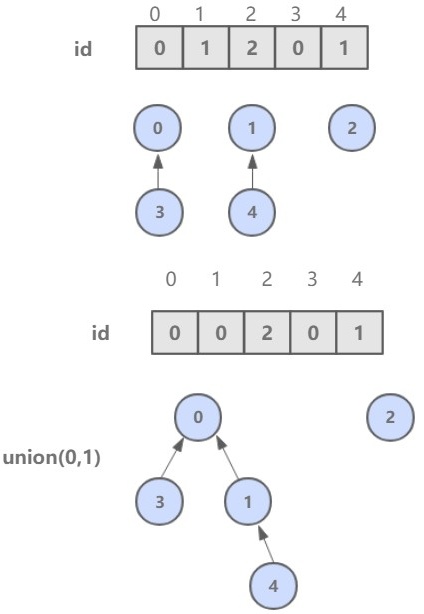
Weighted Quick Union
In order to solve the problem that the tree of quick union is usually very high, weighted quick Union will connect smaller trees to larger trees during union operation.
Theoretical research shows that the depth of the tree constructed by the weighted quick union algorithm does not exceed logN at most.
public class WeightedQuickUnionUF extends UF {
// Save node quantity information
private int[] sz;
public WeightedQuickUnionUF(int N) {
super(N);
this.sz = new int[N];
for (int i = 0; i < N; i++) {
this.sz[i] = 1;
}
}
@Override
public int find(int p) {
while (p != id[p]) {
p = id[p];
}
return p;
}
@Override
public void union(int p, int q) {
int i = find(p);
int j = find(q);
if (i == j) return;
if (sz[i] < sz[j]) {
id[i] = j;
sz[j] += sz[i];
} else {
id[j] = i;
sz[i] += sz[j];
}
}
}
Weighted Quick Union for path compression
While checking the nodes, link them directly to the root node, just add a loop in find.
compare
| algorithm | union | find |
|---|---|---|
| Quick Find | N | 1 |
| Quick Union | Tree height | Tree height |
| Weighted Quick Union | logN | logN |
| Weighted Quick Union for path compression | Very close to 1 | Very close to 1 |