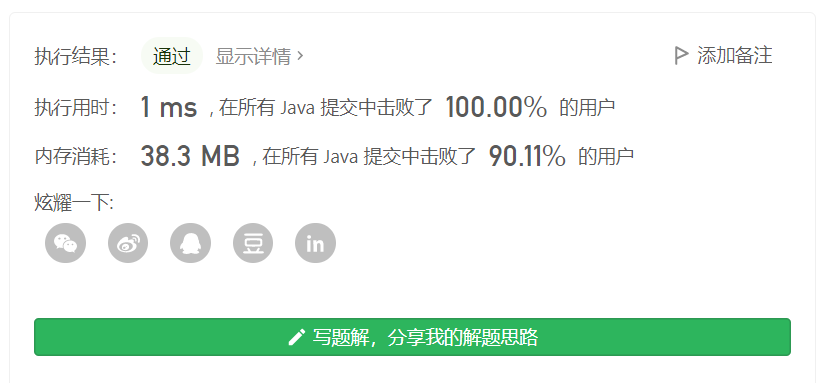
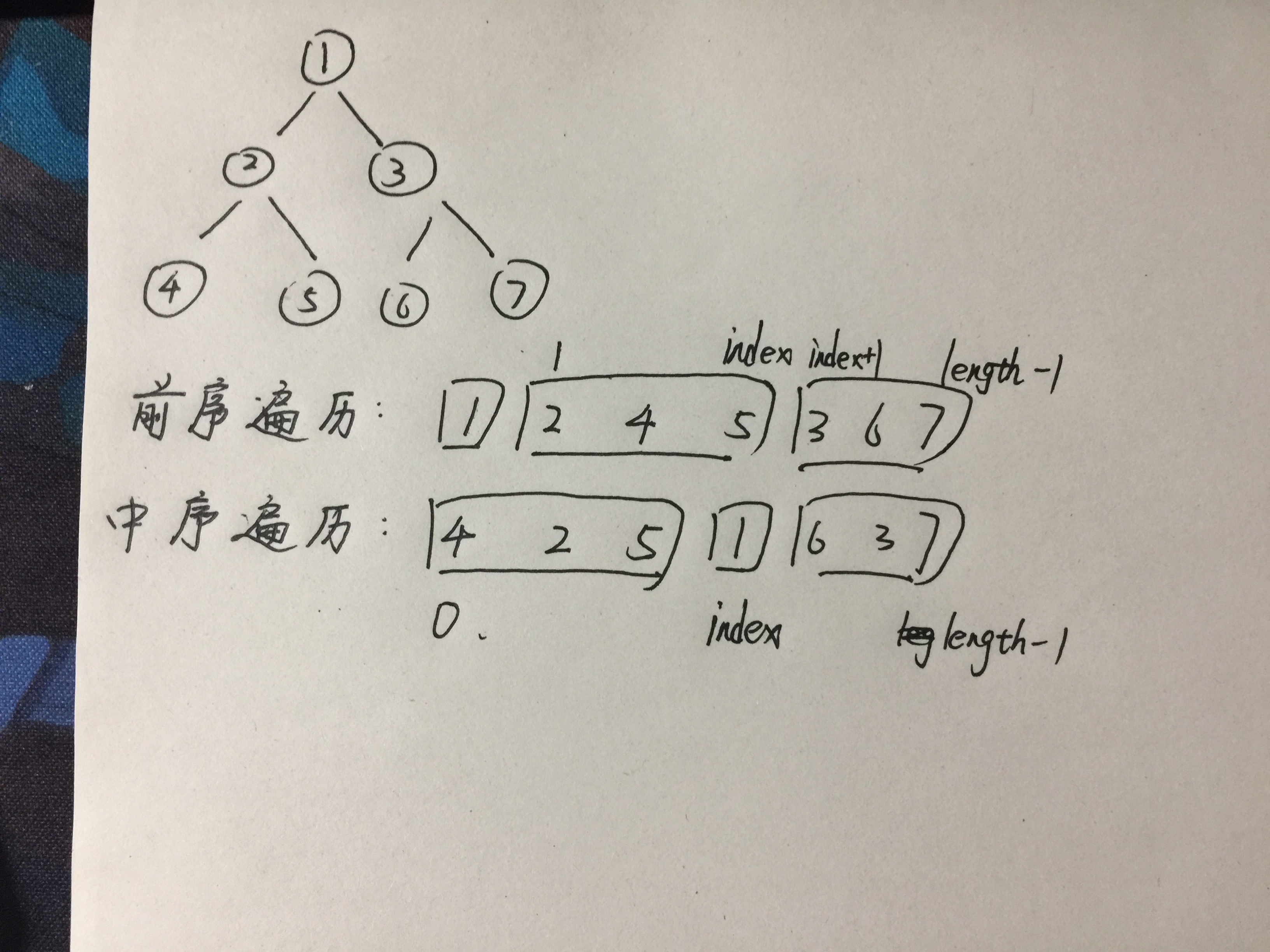
Method 1: recursion, starting from the root node, regards each node under the root node as the root node (the idea of recursion), and then according to the characteristics of preorder traversal, the first value of the traversal result is the value of the root node. Therefore, the recursive assignment process can be determined, and then the positions of preorder traversal and middle order traversal of the confirmation, The binary tree is constructed recursively for (pre order traversal of the left subtree, middle order traversal of the left subtree) and (pre order traversal of the right subtree, middle order traversal of the right subtree). Another important point here is to find the index of the value of the root node in the middle order traversal through the value of the root node in the previous order traversal, so as to divide the left subtree and right subtree in the middle order traversal.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if(preorder == null || preorder.length == 0){
            return null;
        }
        TreeNode root = new TreeNode(preorder[0]);
        
        int index = getIndex(preorder,inorder);

        //Note that copyOfRange() is a left closed right open interval
        root.left = buildTree(Arrays.copyOfRange(preorder,1,index+1),Arrays.copyOfRange(inorder,0,index));
        root.right = buildTree(Arrays.copyOfRange(preorder,index+1,preorder.length),Arrays.copyOfRange(inorder,index+1,inorder.length));
        return root;
    }
    public int getIndex(int[] preorder,int[] inorder){
        int index = 0;
        for(int i = 0;i<inorder.length;i++){
            if(inorder[i] == preorder[0]){
                index = i;
            }
        }
        return index;
    }
    
}

Time complexity: O(n), number of tree nodes
Space complexity: O(1)

Method 2: using iterative method

What is iterative method? Iterative method is to traverse the binary tree in a non recursive form. Like recursive method, iterative method is also divided into three iterative methods: pre order, middle order and post order. The specific method of iterative method is to use a stack to temporarily store the nodes in the binary tree and a result array to store the final traversal results.

Use the iterative method to realize the preorder traversal of binary tree (about the root)

	public List<Integer> preorderTraversal(TreeNode root){
		Deque<TreeNode> stack = new LinkedList<TreeNode>();
		if(root == null){return result;}
		List<Integer> result = new ArrayList<Integer>();
		stack.push(root);
		while(!stack.isEmpty()){
			TreeNode node = stack.peek();
			result.add(node.val);
			if(node.right!=null){stack.push(node.right);}
			if(node.left!=null){stack.push(node.left);}
		}
		return result;
	}

Application of iterative method in this problem: use a stack to temporarily store the elements in the pre order traversal. When it is necessary to build the left subtree, the top element of the stack has a feature that the top element of the stack is not equal to the inorder(index), so there is the following idea.

1. Go through preorder from 1, and [compare whether the elements at the top of the stack and inorder[index] are equal each time],
2. If not equal: preorder[i] is stacked and becomes a left subtree;
3. If equal: pop up the stack top element, index + 1;
4. In this way, it pops up until the top element of the stack is not equal to inorder[index], and the preorder[I] becomes a right subtree. (indicates the leftmost side of a left subtree)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if(preorder.length == 0|| inorder.length == 0){
            return null;
        }
        //Build root node
        TreeNode root = new TreeNode(preorder[0]);
        //Use stack as auxiliary
        Deque<TreeNode> stack = new LinkedList<TreeNode>();

        //Initialize the stack and put the root node into the stack
        stack.push(root);
        //Traversal index of medium order traversal
        int index = 0; 

        //Traverse the pre order array from 1
        for(int i = 1;i < preorder.length;i++){
    
            //Take out the top element of the stack
            TreeNode node = stack.peek();
        //When the values of the top node of the stack and the inorder index are not equal, preorder[i] is the left child node of the top node of the stack
            if(node.val != inorder[index]){
                node.left = new TreeNode(preorder[i]);
                stack.push(node.left);
            }else{
                    //When the value of the top node of the stack is equal to that of the inorder index, it indicates that it has reached the far left. Therefore, pop up the top node of the stack to make room for the right node. At the same time, move the inorder index until the value of the top node of the stack is not equal to that of the inorder[index], you can start to build the right node
                while(!stack.isEmpty() && stack.peek().val == inorder[index]){
                        node = stack.pop();
                        index++;
                    }
                    //
                    node.right = new TreeNode(preorder[i]);
                    stack.push(node.right);
                }
            }
        return root;
    }
}

Method 3: recursive + hash optimization

class Solution {
    private Map<Integer, Integer> indexMap;

    public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
        if (preorder_left > preorder_right) {
            return null;
        }

        // The first node in the preorder traversal is the root node
        int preorder_root = preorder_left;
        // Locate the root node in the middle order traversal
        int inorder_root = indexMap.get(preorder[preorder_root]);
        
        // First establish the root node
        TreeNode root = new TreeNode(preorder[preorder_root]);
        // Get the number of nodes in the left subtree
        int size_left_subtree = inorder_root - inorder_left;
        // The left subtree is constructed recursively and connected to the root node
        // The elements "size_left_subtree starting from the left boundary + 1" in the preorder traversal correspond to the elements "from the left boundary to the root node location - 1" in the inorder traversal
        root.left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
        // The right subtree is constructed recursively and connected to the root node
        // The element "starting from the left boundary + 1 + number of left subtree nodes to the right boundary" in the preorder traversal corresponds to the element "locating from the root node + 1 to the right boundary" in the preorder traversal
        root.right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
        return root;
    }

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = preorder.length;
        // Construct hash mapping to help us quickly locate the root node
        indexMap = new HashMap<Integer, Integer>();
        for (int i = 0; i < n; i++) {
            indexMap.put(inorder[i], i);
        }
        return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
    }
}

Use hash table to establish mapping and change space for time. If method 1 is used, two new pre order traversal arrays and middle order traversal arrays are passed in each recursion. It is inconvenient to obtain the index, because the obtained index is the index of the new preorder[0] in the old inorder, and what we need is a new index. My ability is insufficient, I haven't thought of how to build a map index on the basis of Fayi for the time being. If anyone thinks of it, please leave a message in the comment area. Thank you!!!

Iterative method: reduction
In fact, the fourth method is the recursive form of idea 3. We don't need an auxiliary stack to maintain the parent node. We can only ensure that the recursive order is left first and then right, and then pass in the value of the parent node as a parameter. This idea is more concise than idea 3 and has a deeper understanding of recursion

class Solution {
    private int in = 0;
    private int pre = 0;
    private int[] preorder;
    private int[] inorder;

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        this.preorder = preorder;
        this.inorder = inorder;
        return build(Integer.MIN_VALUE);
    }

    private TreeNode build(int stop) {
        if (pre >= preorder.length)
            return null;
        if (inorder[in] == stop) {
            in++;
            return null;
        }
        TreeNode node = new TreeNode(preorder[pre++]);
        node.left = build(node.val);
        node.right = build(stop);
        return node;
    }
}

Method 4 Author: Yun Yu Chen
Link: https://leetcode-cn.com/problems/zhong-jian-er-cha-shu-lcof/solution/si-chong-si-lu-shen-ru-yu-qian-chu-di-gu-53eh/