Algorithms Series 15 Days Quick - Seven Classic Sorting on the Third Day

Posted by p4rsec on Fri, 17 May 2019 12:58:11 +0200

Algorithms Series 15 Days Quick - Seven Classic Sorting on the Third Day


From: http://blog.csdn.net/m13666368773/article/details/7506678

Today I'm going to talk about the last three sorts of sorting: direct insertion sort, Hill sort and merge sort.

 

Direct insertion sort:

This sort is quite understandable. A real example is that we fight against landlords. When we catch a hand of random cards, we have to sort out the cards according to their size. After 30 seconds,

After carding poker, 4 3, 5 s, wow... recall how we did it.

The leftmost card is 3, the second card is 5, and the third card is 3. Put it behind the first card and the fourth card is 3.

The fifth card is 3, ecstasy, haha, a gun came into being.

 

Well, there are algorithms everywhere in our life, which have already been integrated into our life and blood.

     

Following is the illustration of the above picture:

             

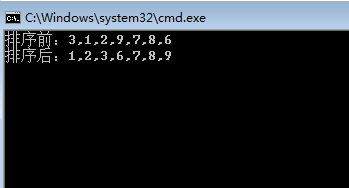
Look at this picture, I don't know if you can understand that in insertion sort, arrays are divided into two kinds: ordered array blocks and disordered array blocks.

     

Yes, on the first pass, a number 20 is extracted from the Unordered Array Block as an ordered array block.

On the second pass, an orderly number of 60 is extracted from the "disordered array block" and placed in the "ordered array block", that is, 20,60.

The third time, the same thing happens, except that 10 is found to be smaller than the value of an ordered array, so 20, 60 positions are moved backwards and a position is set aside for 10 to insert.

Then you can insert all of them according to this rule.

  

  1. using System;  
  2.  using System.Collections.Generic;  
  3.  using System.Linq;  
  4.  using System.Text;  
  5.    
  6.  namespace InsertSort  
  7.  {  
  8.      public class Program  
  9.      {  
  10.          static void Main(string[] args)  
  11.          {  
  12.              List<int> list = new List<int>() { 3, 1, 2, 9, 7, 8, 6 };  
  13.    
  14.              Console.WriteLine("Before sorting:" + string.Join(",", list));  
  15.    
  16.              InsertSort(list);  
  17.    
  18.              Console.WriteLine("After sorting:" + string.Join(",", list));  
  19.          }  
  20.    
  21.          static void InsertSort(List<int> list)  
  22.          {  
  23.              //No sequence  
  24.              for (int i = 1; i < list.Count; i++)  
  25.              {  
  26.                  var temp = list[i];  
  27.    
  28.                  int j;  
  29.    
  30.                  //Ordered sequence  
  31.                  for (j = i - 1; j >= 0 && temp < list[j]; j--)  
  32.                  {  
  33.                      list[j + 1] = list[j];  
  34.                  }  
  35.                  list[j + 1] = temp;  
  36.              }  
  37.          }  
  38.      }  
  39.  }  

 

Hill Sort:

Watch Insert Sort: It's not hard to see that she has a weakness:

If the data is "5, 4, 3, 2, 1", then we insert the records in the "disordered block" into the "ordered block", we estimate that we are going to crash.

Move the position every time you insert, and the efficiency of insertion sort can be imagined.

   

Based on this weakness, shell has improved its algorithm and incorporated an idea called "Reduced Incremental Sorting", which is actually quite simple, but a little noteworthy is that:

Increments are not arbitrary, but regular.

First of all, we need to clarify the method of increment.

The first increment is d=count/2;

The second increment is d=(count/2)/2;

Last until: d=1;

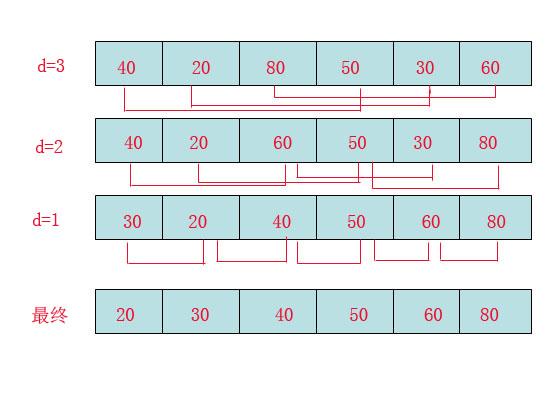
The phenomena observed in the picture above are as follows:

d=3:40 to 50, because 50 is big, no exchange.

Compare 20 to 30, because 30 is big, no exchange.

Compare 80 to 60, because 60 is small, exchange.

d=2:40 to 60, no exchange, 60 to 30, then 30 is smaller than 40, and 40 and 30 are exchanged, as shown above.

Make 20 to 50, no exchange, continue to make 50 to 80, no exchange.

d=1: This is the insertion sort mentioned earlier, but the sequence is almost ordered at this time, which brings a great performance improvement to the insertion sort.

 

Since Hill Sorting is an improved version of Insert Sorting, how much faster can we get in a wh number than that?

 

Here's a test:

View Code
  1. View Code   
  2.  using System;  
  3.  using System.Collections.Generic;  
  4.  using System.Linq;  
  5.  using System.Text;  
  6.  using System.Threading;  
  7.  using System.Diagnostics;  
  8.    
  9.  namespace ShellSort  
  10.  {  
  11.      public class Program  
  12.      {  
  13.          static void Main(string[] args)  
  14.          {  
  15.              //The 5 Comparison  
  16.              for (int i = 1; i <= 5; i++)  
  17.              {  
  18.                  List<int> list = new List<int>();  
  19.    
  20.                  //Insert 1w random numbers into the array  
  21.                  for (int j = 0; j < 10000; j++)  
  22.                  {  
  23.                      Thread.Sleep(1);  
  24.                      list.Add(new Random((int)DateTime.Now.Ticks).Next(10000, 1000000));  
  25.                  }  
  26.    
  27.                  List<int> list2 = new List<int>();  
  28.                  list2.AddRange(list);  
  29.    
  30.                  Console.WriteLine("\n The first" + i + "Secondary comparison:");  
  31.    
  32.                  Stopwatch watch = new Stopwatch();  
  33.    
  34.                  watch.Start();  
  35.                  InsertSort(list);  
  36.                  watch.Stop();  
  37.    
  38.                  Console.WriteLine("\n The time spent inserting sort:" + watch.ElapsedMilliseconds);  
  39.                  Console.WriteLine("Top Ten Numbers of Output:" + string.Join(",", list.Take(10).ToList()));  
  40.    
  41.                  watch.Restart();  
  42.                  ShellSort(list2);  
  43.                  watch.Stop();  
  44.    
  45.                  Console.WriteLine("\n Hill Sorting takes time:" + watch.ElapsedMilliseconds);  
  46.                  Console.WriteLine("Top Ten Numbers of Output:" + string.Join(",", list2.Take(10).ToList()));  
  47.    
  48.              }  
  49.          }  
  50.    
  51.          ///<summary>  
  52.  /// Hill sort  
  53.  ///</summary>  
  54.  ///<param name="list"></param>  
  55.          static void ShellSort(List<int> list)  
  56.          {  
  57.              //Increment  
  58.              int step = list.Count / 2;  
  59.    
  60.              while (step >= 1)  
  61.              {  
  62.                  //No sequence  
  63.                  for (int i = step; i < list.Count; i++)  
  64.                  {  
  65.                      var temp = list[i];  
  66.    
  67.                      int j;  
  68.    
  69.                      //Ordered sequence  
  70.                      for (j = i - step; j >= 0 && temp < list[j]; j = j - step)  
  71.                      {  
  72.                          list[j + step] = list[j];  
  73.                      }  
  74.                      list[j + step] = temp;  
  75.                  }  
  76.                  step = step / 2;  
  77.              }  
  78.          }  
  79.    
  80.          ///<summary>  
  81.  /// Insertion sort  
  82.  ///</summary>  
  83.  ///<param name="list"></param>  
  84.          static void InsertSort(List<int> list)  
  85.          {  
  86.              //No sequence  
  87.              for (int i = 1; i < list.Count; i++)  
  88.              {  
  89.                  var temp = list[i];  
  90.    
  91.                  int j;  
  92.    
  93.                  //Ordered sequence  
  94.                  for (j = i - 1; j >= 0 && temp < list[j]; j--)  
  95.                  {  
  96.                      list[j + 1] = list[j];  
  97.                  }  
  98.                  list[j + 1] = temp;  
  99.              }  
  100.          }  
  101.      }  
  102.  }  


The screenshots are as follows:

 

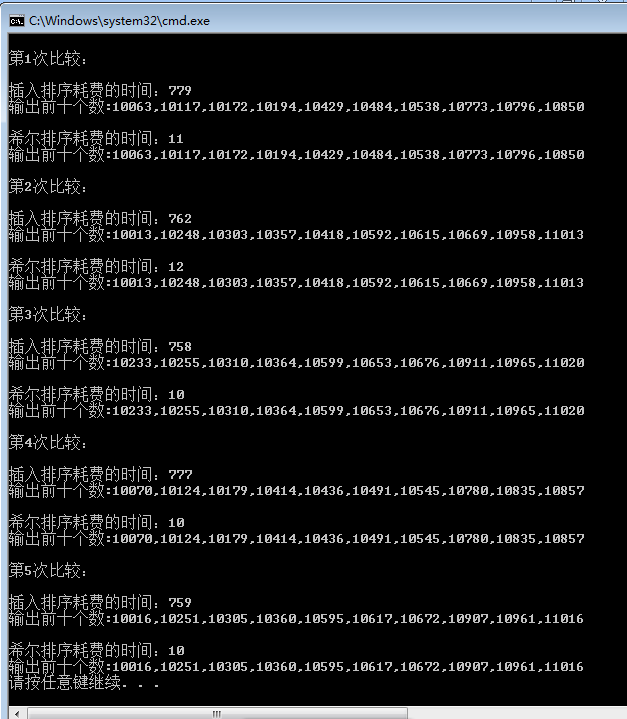
As you can see, Hill ranking has been optimized a lot. In w ranking, the difference is more than 70 times wow.

 

Merge Sort:

Personally, the sorting that we can easily understand is basically O (n^2), and the sorting that is more difficult to understand is basically N(LogN), so merge sorting is also more difficult to understand, especially in code.

Writing, I just did it all afternoon, giggling.

 

First look at the picture:

There are two things to do in merging and sorting:

The first is "score", which is to divide arrays as much as possible up to the atomic level.

The second is "union", which combines two or two atomic levels and produces results.

Code:

  1. using System;  
  2.  using System.Collections.Generic;  
  3.  using System.Linq;  
  4.  using System.Text;  
  5.    
  6.  namespace MergeSort  
  7.  {  
  8.      class Program  
  9.      {  
  10.          static void Main(string[] args)  
  11.          {  
  12.              int[] array = { 3, 2, 1, 8, 9, 0 };  
  13.    
  14.              MergeSort(array, new int[array.Length], 0, array.Length - 1);  
  15.    
  16.              Console.WriteLine(string.Join(",", array));  
  17.          }  
  18.    
  19.          ///<summary>  
  20.  /// Array partition  
  21.  ///</summary>  
  22.  /// <param-name="array">array to be sorted </param>  
  23.  /// <param-name="temparray">temporary storage array </param>  
  24.  /// <param-name="left">the starting position of sequence segment,</param>  
  25.  /// <param-name="right">end position of sequence segment </param>  
  26.          static void MergeSort(int[] array, int[] temparray, int left, int right)  
  27.          {  
  28.              if (left < right)  
  29.              {  
  30.                  //Segmentation location  
  31.                  int middle = (left + right) / 2;  
  32.    
  33.                  //Recursively partitioning the left sequence of arrays  
  34.                  MergeSort(array, temparray, left, middle);  
  35.    
  36.                  //Recursively partitioning the right sequence of arrays  
  37.                  MergeSort(array, temparray, middle + 1, right);  
  38.    
  39.                  //Number combination and operation  
  40.                  Merge(array, temparray, left, middle + 1, right);  
  41.              }  
  42.          }  
  43.    
  44.          ///<summary>  
  45.  /// Binary merging of arrays  
  46.  ///</summary>  
  47.  /// <param-name="array">array to be sorted </param>  
  48.  /// <param-name="temparray">temporary array </param>  
  49.  /// <param-name="left">the starting position of the first interval segment </param>  
  50.  /// <param. name="middle">the starting position of the second interval </param>  
  51.  /// <param-name="right">end position of the second interval </param>  
  52.          static void Merge(int[] array, int[] temparray, int left, int middle, int right)  
  53.          {  
  54.              //Left pointer end  
  55.              int leftEnd = middle - 1;  
  56.    
  57.              //Right finger needle  
  58.              int rightStart = middle;  
  59.    
  60.              //Subscription of Temporary Array  
  61.              int tempIndex = left;  
  62.    
  63.              //length Length after Combination of Numbers  
  64.              int tempLength = right - left + 1;  
  65.    
  66.              //The case where neither interval of the first cycle ends  
  67.              while ((left <= leftEnd) && (rightStart <= right))  
  68.              {  
  69.                  //If an ordered column is found to be large, it is placed in a temporary array  
  70.                  if (array[left] < array[rightStart])  
  71.                      temparray[tempIndex++] = array[left++];  
  72.                  else  
  73.                      temparray[tempIndex++] = array[rightStart++];  
  74.              }  
  75.    
  76.              //Judging whether the left sequence ends  
  77.              while (left <= leftEnd)  
  78.                  temparray[tempIndex++] = array[left++];  
  79.    
  80.              //Judging whether the right sequence ends  
  81.              while (rightStart <= right)  
  82.                  temparray[tempIndex++] = array[rightStart++];  
  83.    
  84.              //Exchange data  
  85.              for (int i = 0; i < tempLength; i++)  
  86.              {  
  87.                  array[right] = temparray[right];  
  88.                  right--;  
  89.              }  
  90.          }  
  91.      }  
  92.  }  

Results:

 

ps: The time complexity of insertion sort is: O(N^2)

The time complexity of Hill sort is: O(N^3/2)

Worst: O(N^2)

The time complexity of merge sort is O(NlogN)

Spatial complexity: O(N)


Topics: shell

Hot Topics

©2024 Programmer Think