All algorithms for breadth and depth traversal of binary tree

For the traversal of binary tree, there are two categories: breadth traversal and depth traversal. For depth traversal, it is divided into first order, middle order and second order. These three first, middle and second order can be written by recursive and non recursive algorithms. The following summarizes these two types of algorithms respectively. In case of this problem in the future, you can use the following template.

Breadth first traversal of binary tree

Breadth first traversal is also called hierarchy traversal, which traverses the binary tree from top to bottom, left to right, layer by layer.
The general flow of the algorithm is as follows:

• An empty queue is established to store the nodes to be traversed. Initially, the parameters of the function (usually the root node) are added to the queue
• When the queue is not empty, it enters the loop
  1. Take out the queue header node and perform relevant processing operations on the obtained node
  2. Judge that if the left child node of the node is not empty, the left child node will be added to the queue
  3. Judge that if the right child node of the node is not empty, the right child node will be added to the queue
• Exit the loop and return parameters if necessary
  Note: if the number of layers needs to be used, first calculate the queue length (number of nodes per layer) when entering the loop, and then put the operations in the above loop into a for loop, which is controlled by the number of nodes per layer
  For example 🌰 : 104. Maximum depth of binary tree
  In this problem, find the depth of the binary tree, that is, in order to find the number of layers of the binary tree, we can use the breadth traversal algorithm. For each layer, add 1 to the depth. I have explained the process above. Next, look at the code. If you encounter this type of problem in the future, you can use the following code as a template.

class Solution(object):
    def maxDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        """breadth-first search """
        if root is None:
        	return 0
        depth = 0
        queue = collections.deque()  # Create an empty queue to store the nodes to be traversed
        queue.append(root)  # Initially, the parameters of the function (usually the root node) are added to the queue
        # Enter the loop when the queue is not empty
        while queue:
        	# Find the number of nodes in each layer
        	size = len(queue)
        	# For each layer, add 1 to the depth
        	depth += 1
        	# Control a for loop with the number of nodes per layer
        	for i in range(size):
        		# Fetch queue header node
        		node = queue.pop()  
        		# Left child node of judgment node
        		if node.left:
        			queue.append(node.left)
        		# Right child node of judgment node
        		if node.right:
        			queue.append(node.right)
        return depth
        

Depth first traversal of binary tree

Depth first traversal of binary trees includes three types: first order (left and right roots), middle order (left and right roots), and second order (left and right roots). For the first order, the root node is processed first, and then to the left subtree of the root node, and then to the right subtree. The left subtree is also regarded as a binary tree, which is still processed according to the left and right of the root. For the middle order, first look at the left subtree of the root node. Similarly, the left subtree is also regarded as a binary tree, which is processed according to the left root and right. Similarly, the later order is first the left subtree, then the right subtree, and finally the root.
The following post order traversal is taken as an example. The post order traversal process is shown in figures (a)~(f). First, if the left subtree of root node 3 is a single node 9, it will directly output 9; Then look at the right subtree. As a whole, if the right subtree is a binary tree with 2 as the root node, first look at its left subtree. If the left subtree is a single node 1, it will output 1, then to the right is a single node 7, it will output 7, and finally to the root node 2. Here, the traversal of the right subtree with 3 as the root node is completed; Finally, go to root node 3 and output 3.

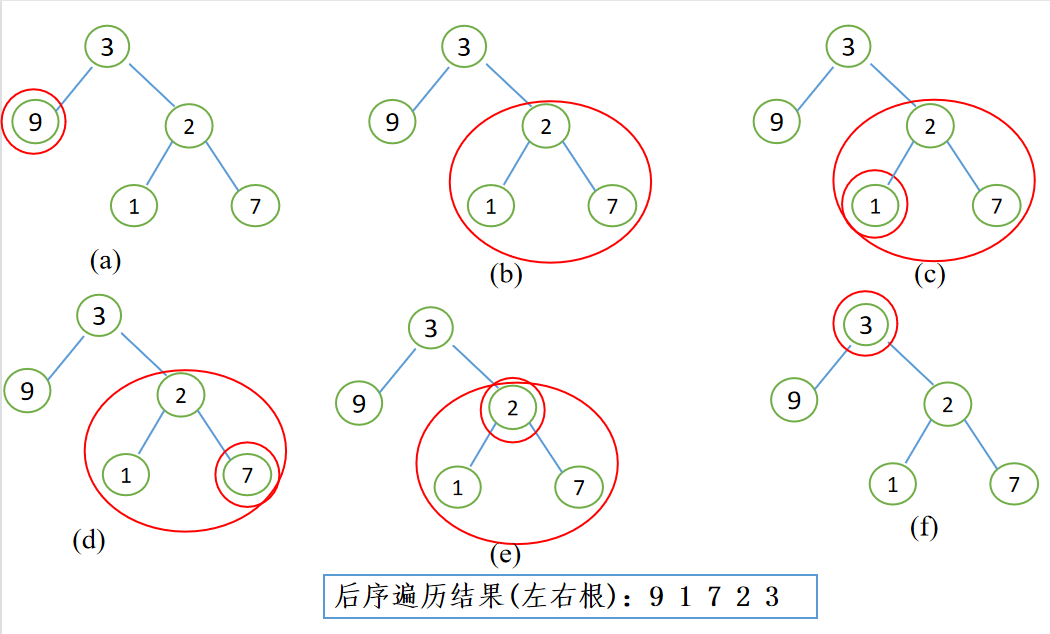
Recursive and non recursive algorithms are introduced below.

Recursive depth first traversal

Depth first traversal is relatively simple to write in recursive form. Generally, there are three main steps of recursion:

1. Recursive termination condition
2. Recursive parameters and return values
3. Single layer recursive logic

For first in order, it is obvious that the recursive termination condition is to terminate when the encountered node is empty; The parameter of the whole function is a node of the incoming binary tree (generally the root node), while the recursive parameter is the left (right) child node of the root node; The logic of recursion is related to the order of traversal.
The general flow of the algorithm is as follows:

• If the node node is empty, exit (recursive termination condition) is returned
• Recursively call itself, and the passed in parameter is node.left (left)
• Recursively call itself, and the passed in parameter is node.right (right)
• Process root node (root)
  The above is the general flow of the later order algorithm. If it is the first order, the root node is processed first, and then the left and right nodes are called recursively. If it is the middle order, the left node is recursive first, then the root node is processed, and then the right node is recursive. In fact, the above execution order is changed.

code

class Solution(object):
	def preorder(self, node):
		"""Recursive depth first traversal (about the first order root)"""
		if node is None:
			return
		print(node.item, end = '')  # Process root node
		self.preorder(node.left)  # Recursive left node
		self.preorder(node.right)  # Recursive right node
		
	def inorder(self, node):
		"""Recursive depth first traversal (middle order left root right)"""
		if node is None:
			return
		self.preorder(node.left)  # Recursive left node
		print(node.item, end = '')  # Process root node
		self.preorder(node.right)  # Recursive right node
		
	def postorder(self, node):
		"""Recursive depth first traversal (post order left and right roots)"""
		if node is None:
			return
		self.preorder(node.left)  # Recursive left node
		self.preorder(node.right)  # Recursive right node
		print(node.item, end = '')  # Process root node	
		

Non recursive depth first traversal

How to implement depth first traversal in a non recursive way? During recursion, the intermediate results of each recursion are actually saved in a stack inside the computer, so we can also use the stack as an auxiliary structure to save this data instead of recursion.
In many writing methods of non recursive depth traversal, there is no connection between the three methods of first middle and then order. It is still difficult to write one of them and the other two. Unlike recursive depth traversal, just write one of them and change the code order of the other two. In order to solve this problem, let's write a unified writing method, which unifies the front, middle and rear order, so as to facilitate everyone's understanding and memory. The key is: store the accessed node in the stack and the node to be processed (root node) in the stack, but then put a null pointer as a mark; When the element in the stack is popped, if the bounced element is not empty, it will be put into the stack. Only when the bounced element is empty, the next element will be output as the result.
The general flow of the post order algorithm is as follows:

• Initially, create a new list to store the traversal output results, create an empty stack to store nodes, and add the starting parameter node (when it is not empty) to the stack
• When the stack is not empty, enter the loop
  1. Take out the top node of the stack
  2. Judge if the node is not empty
     2.1. Add the node to the stack, and then add a null pointer to the stack (root)
     2.2. If the right child node of a node is not empty, add the right child node to the stack (right)
     2.3. If the left child node of the node is not empty, add the left child node to the stack (left)
  3. Otherwise, if the node is empty, the element at the top of the stack will be taken out and stored in the result list
• Exit the loop and return to the result list
  Pay attention to the stacking order in the above algorithm. If the post order (left and right root), the stacking order is opposite. The root is right and left. Because of the last in first out feature of the stack, it should be stacked in the opposite direction. As for the pre order and middle order, just change the above stacking order.

code

class Solution(object):
	def preorder(self, root)
		"""Non recursive depth first traversal (about the first order root)"""
		result = []
		stack = []
		if root:
			stack.append(root)
		while stack:
			node = stack.pop()
			if node:
				if node.right:
					stack.append(node.right)  # right
				if node.left:
					stack.append(node.left)  # Left
				stack.append(node)  # root
				stack.append(None)  # A null pointer is added after the root
			else:
				r = stack.pop()
				result.append(r.item)
		return result
		
	def inorder(self, root)
		"""Non recursive depth first traversal (middle order left root right)"""
		result = []
		stack = []
		if root:
			stack.append(root)
		while stack:
			node = stack.pop()
			if node:
				if node.right:
					stack.append(node.right)  # right
				stack.append(node)  # root
				stack.append(None)
				if node.left:
					stack.append(node.left)  # Left
			else:
				r = stack.pop()
				result.append(r.item)
		return result
		
	def postorder(self, root):
		"""Non recursive depth first traversal (post order left and right roots)"""
		result = []
		stack = []
		if root:
			stack.append(root)
		while stack:
			node = stack.pop()
			if node:
				stack.append(node)  # root
				stack.append(None)
				if node.right:
					stack.append(node.right) # right
				if node.left:
					stack.append(node.left)  # Left
			else:
				r = stack.pop()
				result.append(r)
		return result
		

Summary: let's summarize the non recursive depth first traversal, which is nothing more than using the stack to save the accessed node and the node to be processed (root node). When the stack is not empty, enter the loop, take out the top element of the stack for judgment, and enter the stack when the element is not empty (the stack entry is in the reverse order of the middle first and then the order. If the order first is about the root, the stack entry is the right and left root, and a null pointer is added after the root node as a mark). When the element is empty, the next element is taken out of the stack as the output result.