QuantLib Financial Calculations: A Case Study of Ordinary Interest Rate Interchange (2)
Summary
The functions involved in interest rate swap in QuantLib fall into two broad categories:
- Valuation of existing interest rate exchange contracts;
- Estimate the implied term structure based on the transaction quotation of interest rate swap contracts.
These two types of functions are closely linked, and the term structure derived from the latest quotation can often be used to estimate the viability of a contract.
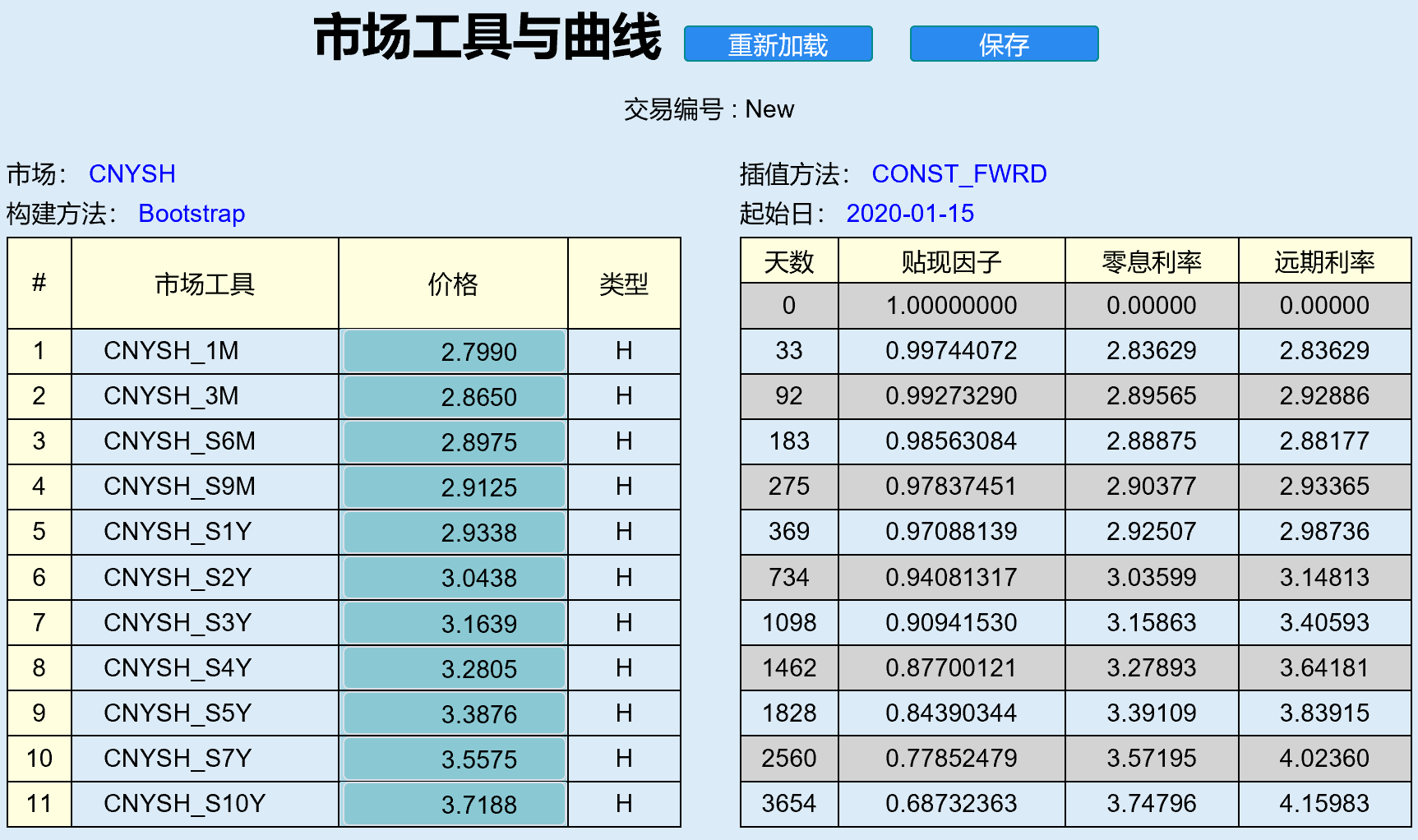
This paper then describes how to deduce the implied interest period structure based on the contract quotation and uses the Technical Documentation of CITIC Constructive Model of Interest Rate Exchange Discount Factor Curve The results of Figure 16 in Fig. 1 are used as a baseline.
Results of Figure 16:
Contract Terms
The process of calculating the term structure through contract quotation is called bootstrap, which is very similar in thought and practice to the mathematical induction used in theoretical proof. The general process is as follows:
- First, the known interest rates and financial instruments to be used are listed in ascending order by duration.
- Assume that the \(n\) value of the term structure has been obtained \(TS_n\), corresponding to the \(n\) quotation;
- Ling\(TS_{n+1}\) is a pending parameter \(x\) and is given an initial value;
- Using known term structure data \(TS_1,\dots,TS_n,x\), Value the \(n+1\) financial instrument;
- Adjust \(x\) so that the valuation results are consistent with the quotation and there is no arbitrage space;
- At this point, \(x\) is \(TS_{n+1}\
- And so on.
Among them, \(TS\) can be any of the three interest rates: spot interest rate, forward interest rate, discount factor, and there are many different interpolation methods available, such as linear interpolation, spline interpolation, logarithmic linear interpolation and constant interpolation.There are many combinations of the two dimensions, and QuantLib uses template technology to achieve a free combination of the two dimensions, depending on the business needs.
It is important to note that the valuation of interest rate swaps is sensitive to the terms of the contract.
The contracts in the example are all Shibor 3M rate exchanges with the following terms and conditions:
- Floating interest rate: Shibor 3M
- Spread: 0.0%
- Valuation date: 2020-01-15
- Settlement delay: 1 day
- Reset delay: 1 day
- Floating End Payment Frequency: Quarter
- Floating End Days Calculation Rule: ACT/360
- Fixed-end payment frequency: Quarterly
- Fixed End Days Calculation Rule: ACT/365
- Calendar: China Interbank Market
- Workday conversion rule: Modified Following (MFL)
practice
For complete code, see the QuantLibEx project's example.cpp File.
using namespace QuantLib;
using namespace std;
Calendar calendar = China(China::IB);
Date today(15, January, 2020);
Settings::instance().evaluationDate() = today;
Natural delayDays = 1;
Date settlementDate = calendar.advance(
today, delayDays, Days);
// must be a business day
settlementDate = calendar.adjust(settlementDate);
cout << "Today: " << today << endl;
cout << "Settlement date: " << settlementDate << endl;
Today: January 15th, 2020 Settlement date: January 16th, 2020
Set RateHelper
The core of bootstrap calculation in QuantLib is to configure RateHelper objects for the PiecewiseYieldCurve template class, which is derived from different financial instruments.The DepositRateHelper class is usually used for known interest rates, and the SwapRateHelper class is used for general interchanges.
Instead of using the Shibor class provided by QuantLib, the sample reconfigured an object on its own according to the contract.(Looking at the source code, this is actually how the IborIndex derived classes in QuantLib are generally constructed)
In addition, Actual365_25 is not provided in QuantLib. To implement it by yourself, it is almost a duplicate of Actual365Fixed.
DayCounter termStrcDayCounter = Actual365_25();
Period mn1(1, Months), mn3(3, Months), mn6(6, Months), mn9(9, Months),
yr1(1, Years), yr2(2, Years), yr3(3, Years), yr4(4, Years),
yr5(5, Years), yr7(7, Years), yr10(10, Years);
ext::shared_ptr<Quote>
m1Rate(new SimpleQuote(2.7990 / 100.0)),
m3Rate(new SimpleQuote(2.8650 / 100.0)),
s6mRate(new SimpleQuote(2.8975 / 100.0)),
s9mRate(new SimpleQuote(2.9125 / 100.0)),
s1yRate(new SimpleQuote(2.9338 / 100.0)),
s2yRate(new SimpleQuote(3.0438 / 100.0)),
s3yRate(new SimpleQuote(3.1639 / 100.0)),
s4yRate(new SimpleQuote(3.2805 / 100.0)),
s5yRate(new SimpleQuote(3.3876 / 100.0)),
s7yRate(new SimpleQuote(3.5575 / 100.0)),
s10yRate(new SimpleQuote(3.7188 / 100.0));
Handle<Quote>
m1RateHandle(m1Rate),
m3RateHandle(m3Rate),
s6mRateHandle(s6mRate),
s9mRateHandle(s9mRate),
s1yRateHandle(s1yRate),
s2yRateHandle(s2yRate),
s3yRateHandle(s3yRate),
s4yRateHandle(s4yRate),
s5yRateHandle(s5yRate),
s7yRateHandle(s7yRate),
s10yRateHandle(s10yRate);
DayCounter depositDayCounter = Actual360();
ext::shared_ptr<RateHelper>
m1(new DepositRateHelper(
m1RateHandle, mn1, delayDays, calendar,
ModifiedFollowing, false, depositDayCounter)),
m3(new DepositRateHelper(
m3RateHandle, mn3, delayDays, calendar,
ModifiedFollowing, false, depositDayCounter));
Frequency fixedLegFreq = Quarterly;
BusinessDayConvention fixedLegConv = ModifiedFollowing;
DayCounter fixedLegDayCounter = Actual365Fixed();
ext::shared_ptr<IborIndex> shiborIndex(
new IborIndex(
"Shibor", mn3, delayDays, CNYCurrency(),
calendar, Unadjusted, false, Actual360()));
ext::shared_ptr<RateHelper>
s6m(new SwapRateHelper(
s6mRateHandle, mn6, calendar, fixedLegFreq, fixedLegConv,
fixedLegDayCounter, shiborIndex)),
s9m(new SwapRateHelper(
s9mRateHandle, mn9, calendar, fixedLegFreq, fixedLegConv,
fixedLegDayCounter, shiborIndex)),
s1y(new SwapRateHelper(
s1yRateHandle, yr1, calendar, fixedLegFreq, fixedLegConv,
fixedLegDayCounter, shiborIndex)),
s2y(new SwapRateHelper(
s2yRateHandle, yr2, calendar, fixedLegFreq, fixedLegConv,
fixedLegDayCounter, shiborIndex)),
s3y(new SwapRateHelper(
s3yRateHandle, yr3, calendar, fixedLegFreq, fixedLegConv,
fixedLegDayCounter, shiborIndex)),
s4y(new SwapRateHelper(
s4yRateHandle, yr4, calendar, fixedLegFreq, fixedLegConv,
fixedLegDayCounter, shiborIndex)),
s5y(new SwapRateHelper(
s5yRateHandle, yr5, calendar, fixedLegFreq, fixedLegConv,
fixedLegDayCounter, shiborIndex)),
s7y(new SwapRateHelper(
s7yRateHandle, yr7, calendar, fixedLegFreq, fixedLegConv,
fixedLegDayCounter, shiborIndex)),
s10y(new SwapRateHelper(
s10yRateHandle, yr10, calendar, fixedLegFreq, fixedLegConv,
fixedLegDayCounter, shiborIndex));
vector<ext::shared_ptr<RateHelper>> instruments;
instruments.push_back(m1);
instruments.push_back(m3);
instruments.push_back(s6m);
instruments.push_back(s9m);
instruments.push_back(s1y);
instruments.push_back(s2y);
instruments.push_back(s3y);
instruments.push_back(s4y);
instruments.push_back(s5y);
instruments.push_back(s7y);
instruments.push_back(s10y);
Bootstrap
The process of Bootstrap is simple. Selecting Piecewise YieldCurve <ForwardRate, BackwardFlat> here, consistent with the example, gives you a "ladder" forward deadline structure.
ext::shared_ptr<YieldTermStructure> termStrc(
new PiecewiseYieldCurve<ForwardRate, BackwardFlat>(
today,
instruments,
termStrcDayCounter));
Verification
Date curveNodeDate = calendar.adjust(settlementDate + mn1);
cout << setw(4) << curveNodeDate - today << ", "
<< termStrc->discount(curveNodeDate) << ", "
<< termStrc->zeroRate(curveNodeDate, termStrcDayCounter, Continuous).rate() * 100.0
<< endl;
curveNodeDate = calendar.adjust(settlementDate + mn3);
cout << setw(4) << curveNodeDate - today << ", "
<< termStrc->discount(curveNodeDate) << ", "
<< termStrc->zeroRate(curveNodeDate, termStrcDayCounter, Continuous).rate() * 100.0
<< endl;
curveNodeDate = calendar.adjust(settlementDate + mn6);
cout << setw(4) << curveNodeDate - today << ", "
<< termStrc->discount(curveNodeDate) << ", "
<< termStrc->zeroRate(curveNodeDate, termStrcDayCounter, Continuous).rate() * 100.0
<< endl;
curveNodeDate = calendar.adjust(settlementDate + mn9);
cout << setw(4) << curveNodeDate - today << ", "
<< termStrc->discount(curveNodeDate) << ", "
<< termStrc->zeroRate(curveNodeDate, termStrcDayCounter, Continuous).rate() * 100.0
<< endl;
curveNodeDate = calendar.adjust(settlementDate + yr1);
cout << setw(4) << curveNodeDate - today << ", "
<< termStrc->discount(curveNodeDate) << ", "
<< termStrc->zeroRate(curveNodeDate, termStrcDayCounter, Continuous).rate() * 100.0
<< endl;
curveNodeDate = calendar.adjust(settlementDate + yr2);
cout << setw(4) << curveNodeDate - today << ", "
<< termStrc->discount(curveNodeDate) << ", "
<< termStrc->zeroRate(curveNodeDate, termStrcDayCounter, Continuous).rate() * 100.0
<< endl;
curveNodeDate = calendar.adjust(settlementDate + yr3);
cout << setw(4) << curveNodeDate - today << ", "
<< termStrc->discount(curveNodeDate) << ", "
<< termStrc->zeroRate(curveNodeDate, termStrcDayCounter, Continuous).rate() * 100.0
<< endl;
curveNodeDate = calendar.adjust(settlementDate + yr4);
cout << setw(4) << curveNodeDate - today << ", "
<< termStrc->discount(curveNodeDate) << ", "
<< termStrc->zeroRate(curveNodeDate, termStrcDayCounter, Continuous).rate() * 100.0
<< endl;
curveNodeDate = calendar.adjust(settlementDate + yr5);
cout << setw(4) << curveNodeDate - today << ", "
<< termStrc->discount(curveNodeDate) << ", "
<< termStrc->zeroRate(curveNodeDate, termStrcDayCounter, Continuous).rate() * 100.0
<< endl;
curveNodeDate = calendar.adjust(settlementDate + yr7);
cout << setw(4) << curveNodeDate - today << ", "
<< termStrc->discount(curveNodeDate) << ", "
<< termStrc->zeroRate(curveNodeDate, termStrcDayCounter, Continuous).rate() * 100.0
<< endl;
curveNodeDate = calendar.adjust(settlementDate + yr10);
cout << setw(4) << curveNodeDate - today << ", "
<< termStrc->discount(curveNodeDate) << ", "
<< termStrc->zeroRate(curveNodeDate, termStrcDayCounter, Continuous).rate() * 100.0
<< endl;
33, 0.997441, 2.83629 92, 0.992733, 2.89565 183, 0.985631, 2.88875 275, 0.978375, 2.90377 369, 0.970721, 2.94142 733, 0.940822, 3.03969 1097, 0.909515, 3.15787 1462, 0.877015, 3.27853 1828, 0.843917, 3.39077 2560, 0.778373, 3.57473 3654, 0.687352, 3.74755
It is very close to the model results of Jianxin Jinke experts, only one date is inconsistent.
Possible sources of difference
Since the workday conversion rule is MFL and is sensitive to holidays, the calendar class that contains Chinese holidays in QuantLib is China, and the holidays it records may not be consistent with those in the Credit Metal System.
Next step
- Analyze the interest rate swaps for the linked FR007 on the domestic market.
- Analyse the interest rate exchange of the linked LPR in the domestic market.