Stack

Definition of stack

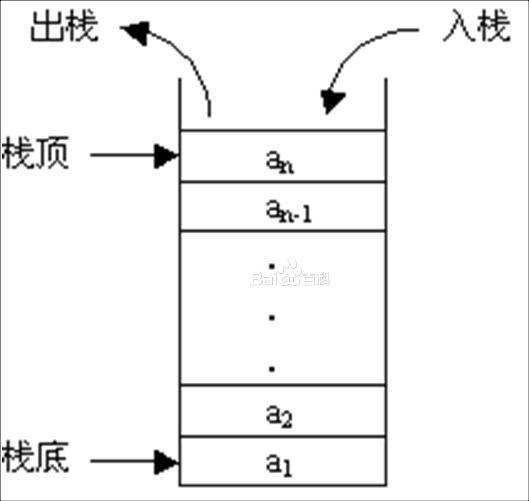
Stack is a linear table with limited operation. It can only enter or output elements from one end. It has the property of * * last in first out (LIFO) * *. The first data is pushed into the bottom of the stack, and the last data is at the top of the stack. When you need to read data, POP up data from the top of the stack (the last data is read out first). The end that allows insertion and deletion is called the top of the stack and the other end is the bottom of the stack; The bottom of the stack is fixed and the top of the stack is floating; When the number of elements in the stack is zero, it is called an empty stack. Insertion is generally called PUSH, and deletion is called POP.

Code implementation of stack

The basic operations of stack mainly include the following: push, pop, query and empty judgment

In the informatics competition, there are two ways to realize the stack loved by players: 1. Realize the handwriting stack with array; 2. Realize it with the template stack in STL

Implementation with array

Define a long enough array a[N], and the variable hh represents the pointer to the top of the stack

//Handwriting stack
#include<iostream>
using namespace std;
const int N=1e5+10;//Set the array length according to the topic requirements 
int stack[N],hh=0;//Initialize the stack, hh is the pointer to the top of the stack 
void push(int x){//Enter the stack 
	stack[++hh]=x;
}
void pop(){//Out of stack 
	if(hh!=0)//Stack is not empty 
		hh--;
} 
bool empty(){//Air judgment 
	if(hh==0) return 1;//If it is empty, return 1 
	return 0;//Non null return 0 
} 
int query(){//Query stack top element 
	if(hh!=0) return stack[hh];//Return stack top element 
}
int main(){
	//Operate the stack according to the topic requirements
	push(3);//Put 3 on the stack
	push(2);//Put 2 on the stack
	pop();//Stack top element out of stack
	if(empty()==1) cout<<"Yes"<<endl;//Empty stack output yes
	else cout<<"No"<<endl; 
	cout<<query()<<endl;//Output stack top element 
	  
} 

Implementation of stack with stl template

stack initialization

The stack in STL is contained in the header file #include < stack >, and a stack is created with the stack < data type > stack name, for example:

Integer( int)						stack<int> s

Floating point type( float,double)			stack<float> q    stack<double> s

Character type( char)					stack<char> s

String type( string)				stack<string> s

Structural type( node(Name of structure)	stack<node> s

Basic operation of stack

s.pop();//Out of stack
s.push(item);s.emplace(args);//Press into the top of the stack
s.top();//Returns the top element of the stack, but does not take the element out of the stack
s.empty();//Air judgment
s.size();//Stack size
s.swap();//Exchange the elements in the current stack with those in the parameters. The elements contained in the parameters must be of the same type as those in the current stack.

example

#include <algorithm> 
#include<iostream>
#include<stack>
using namespace std;
int main()
{
    stack <int>stk;		//Define a stack of int type 
    for(int i=0;i<10;i++){	//Push  
        stk.push(i);
    }
    cout<<"Stack size:"<<stk.size()<<endl;	 
    while(!stk.empty()){	//When stack is not empty 
        cout<<stk.top()<<" ";	//Output stack top 
        stk.pop();		//Delete stack top element 
    }
    cout<<endl;
    cout<<"Stack size:"<<stk.size()<<endl;
    return 0;
}

Note: if the topic involves more operations of entering and leaving the stack, try to write the stack, because it takes a long time to call the STL template and it is easy to timeout

Application of stack

Expression evaluation

One of the great uses of stack is to calculate arithmetic expressions. Arithmetic expressions usually have three expression methods: prefix, infix and suffix

Infix expression: an expression that conforms to human thinking habits, for example: (1-2) * 3

Prefix expression: it is called polish, such as "op A B", OP is the operator, and A and B are the other two prefix expressions, such as * 3 - 1 2

Suffix expression: it is called inverse Polish, such as "A B op", such as 1, 2 - 3*

Prefix and suffix expressions do not need parentheses to determine the operation order. Compared with infix expressions, suffix expressions are more convenient for computer calculation. Because when calculating suffix expressions, the computer only needs to take out two numbers at the top of the stack one by one. If an operator is encountered, it will take out the two numbers at the top of the stack for calculation and put the results into the stack. When there is exactly one number left in the stack, it is the suffix expression This calculation method does not need to consider the operation order, which is more in line with the calculation method of the computer, because human beings can judge which can be calculated first and which can be calculated later at a glance, but the computer can't. the computer can only meet who is who.

Therefore, if you want the computer to solve the value of the infix expression commonly used by human beings, the fastest way is to convert the infix expression into a suffix expression, and then let the computer evaluate it through the suffix expression. This transformation can be completed by stack O(N). Of course, you can also use recursion to solve the value of infix expression. The time complexity is O(N^2) Yes, those who are interested can go down and find it by themselves

Infix to suffix operator

1. Establish a stack for storing operators and scan the elements in the infix expression one by one.

2. If digital direct output is encountered

3. If you encounter an open bracket, put the open bracket on the stack.

4. If you encounter a right bracket, keep taking out the top of the stack and outputting until you encounter an left bracket, and then take the left bracket out of the stack

5. If an operator is encountered, compare it with the operator at the top of the stack. If the priority of the operator at the top of the stack is not lower than the operator, it will be out of the stack and output until the operator at the top of the stack is not lower than the operator, and the operator will be put on the stack

6. When all elements are scanned, the remaining operators in the stack are out of the stack and output.

   #include<iostream>
   #include<string>
   #include<stack>
   #include<cctype>
   using namespace std;
   
   string change(string s){//Infix to suffix 
   	string tmp="";//initialization 
   	stack<char>sta;
   	for(int i=0;i<s.length();i++){
   		if(isdigit(s[i])) tmp+=s[i];//If it's a number 
   		else if(s[i]=='(') sta.push(s[i]);
   		else if(s[i]==')'){
   			while(sta.top()!='('){
   				tmp+=sta.top();
   				sta.pop();
   			}
   			sta.pop();
   		}
   		else{
   			if(s[i]=='*'||s[i]=='/'){
   				while((!sta.empty())&&(sta.top()=='*'||sta.top()=='/')){
   					tmp+=sta.top();
   					sta.pop();
   				}
   				sta.push(s[i]);
   			} 
   			else if(s[i]=='+'||s[i]=='-'){
   					while((!sta.empty())&&(sta.top()=='*'||sta.top()=='/'||sta.top()=='+'||sta.top()=='-')){
   					tmp+=sta.top();
   					sta.pop();
   				}
   				sta.push(s[i]);
   			}
   		}
   	}
   	if(!sta.empty()){
   		while(!sta.empty()){
   			tmp+=sta.top();
   			sta.pop();
   		} 
   	}
   	return tmp;
   }
   int main(){
   	string s;
   	cin>>s;//Enter infix expression
   	cout<<change(s);
   	
   }
   

Suffix expression evaluation

1. Create a stack for storage and scan the elements in the suffix expression one by one

2. If a number is encountered, it is put on the stack

3. If an operator is encountered, take out the two numbers at the top of the stack for calculation and put the result on the stack.

4. After scanning, there is just one number left in the stack, which is the value calculated by the suffix expression

   #include<iostream>
   #include<string>
   #include<stack>
   #include<cctype>
   using namespace std;
   int cal(string s){//Suffix expression calculation is only applicable to the operation of one digit in the suffix 
   	stack<double> sta;
   	for(int i=0;i<s.length();i++){
   		if(isdigit(s[i])) sta.push(s[i]-'0');
   		else{
   			int t1=sta.top();sta.pop();//Number of post stack 
   			int t2=sta.top();sta.pop();//Number of first stacked 
   			cout<<t1<<" "<<t2<<endl;
   			if(s[i]=='-') sta.push(t2-t1);
   			else if(s[i]=='+') sta.push(t2+t1);
   			else if(s[i]=='*') sta.push(t2*t1);
   			else sta.push((double)t2/(double)t1);
   		}
   	}
   	return sta.top();
   }
   int main(){
   	string s;
   	cin>>s; 
   	cout<<cal(s);
   	
   }
   

Please complete the valley of Los Angeles P1981 P1449 P1310 subject

Monotone stack

As the name suggests, the elements in the monotone stack are monotonically ordered, so the monotone stack is divided into monotone increasing stack and monotone decreasing stack

• Monotonically increasing stack: from the top of the stack to the bottom of the stack, elements from small to large
• Monotonically decreasing stack: from the top of the stack to the bottom of the stack, elements from large to small

Monotone stack action

By using monotone stack, we can access the last element larger or smaller than it. In practical application, we need to maintain a monotone stack, which can eliminate impossible options in time by using monotonicity

Monotonically increasing stack: on the premise of monotonically increasing the elements in the stack (if the element at the top of the stack is larger than the element to be put into the stack, it will pop up), put the new element into the stack.

Monotonic decrement stack: on the premise of keeping the monotonic decrement of the elements in the stack (if the element at the top of the stack is smaller than the element to be put into the stack, it will pop up), put the new element into the stack.

Example: given an integer sequence with length N, output the first number smaller than it on the left of each number. If it does not exist, output − 1.

Input format

The first row contains the integer N, which represents the length of the sequence.

The second row contains N integers, representing the integer sequence.

Output format

A total of one line, including N integers, where the ith number represents the first number smaller than it on the left of the ith number. If it does not exist, it outputs − 1.

Data range

1≤N≤10^5
1 ≤ elements in sequence ≤ 10 ^ 9

Input example:

5
3 4 2 7 5

Output example:

-1 3 -1 2 2

analysis

If the violent method is to traverse from this number to its left until the first number to its left is found, the time complexity of this method is O(N^2). The time complexity can be reduced to O(N) by using the monotone stack method

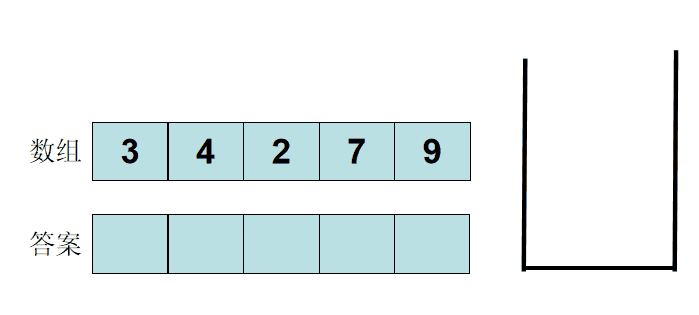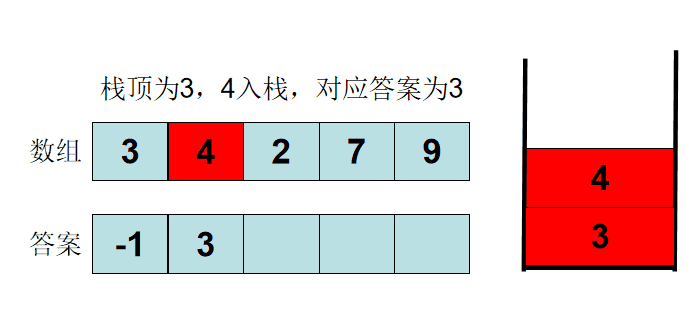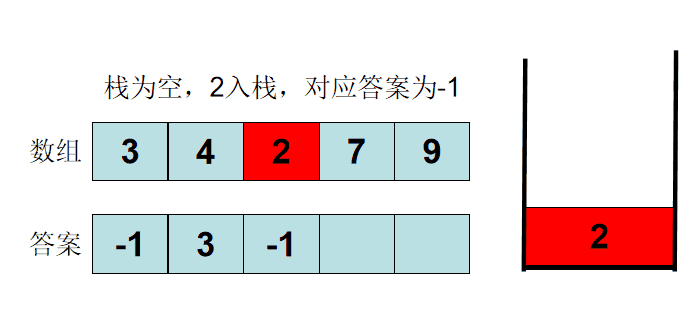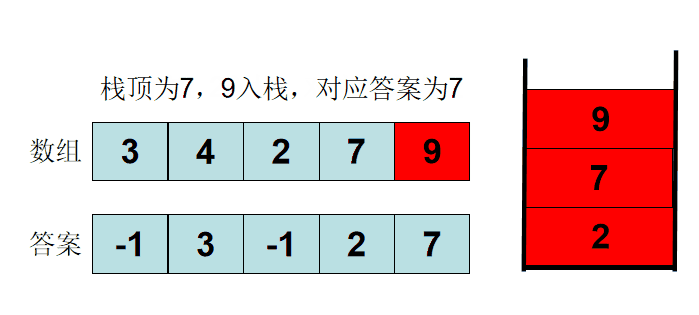
Let's take example 3 4 2 5 7. If the stack is empty, output - 1. If the stack top element is greater than or equal to the new element, exit the stack until the stack is empty or less than the new element. At this time, the stack top is the first number on the left of the new element, output the stack top element, and then put the new element on the stack.

#include<iostream>
using namespace std;
const int N=1e5+10;
int a[N],s[N],tt=0;
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		int x;
		cin>>x;
		while(tt&&s[tt]>=x) tt--;//If it is not empty or the stack top element is larger than the current element, it will be out of the stack
		if(tt==0) cout<<-1<<" ";
		else cout<<s[tt];
		s[++tt]=x;
	}
    
	return 0;
}

Exercises in this section

Look Up S

Largest Rectangle in a Histogram