About hash tables
Concept of hash table
Hash table, also known as hash table, is a data structure that directly accesses the memory storage location according to the key.
Hash tables exist in many high-level languages. For example, in Python, there is a data structure called dict. The Chinese translation is a dictionary, which should be implemented based on hash tables. Let's take looking up a phone number in life as a popular example to explain what a hash table is.
An example of understanding hash tables
We can think of the hash table as a phone book arranged alphabetically by people's names. When we want to find Zhang San's phone number, we can easily know that Zhang San's initials are Z. Ideally, Zhang San may be the first one at the beginning of the phone book Z. if not, he may have to find a few more people in the future.
Obviously, it is much faster to find the phone according to the initials than to find it one by one. This is the characteristic of hash table.
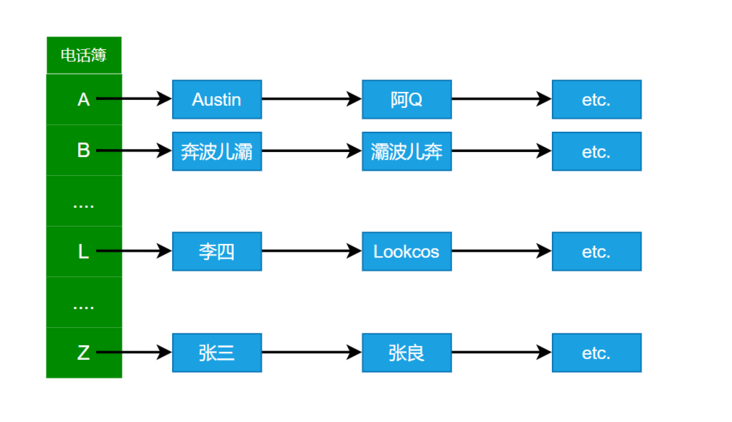
Terms related to the hash table corresponding to the above example:
- Hash table: phonebook
- Key: name, such as Zhang San
- Hash function (F): a method to calculate the initial of a name. The parameter is the name and the return is the corresponding initial
- Hash address: the return value of the hash function. In the example, A-Z can be understood as a hash address
What is conflict
For different keywords, the same hash address may be obtained through the calculation of hash function. For example, although the names of benbo'erba (key1) and babo'erban (key2) are different (key1 ≠ key2), the same result (F(key1)=F(key2)=B) is calculated by the hash function, and the initials of their names are B. This situation is called conflict.
Conflict resolution methods
There are many conflict resolution methods, such as open address method and chain address method, which can be selected according to the specific use scenario. Generally speaking, the chain address method is often used in actual projects and development.
The basic idea of chain address method is to put the keywords of the same hash address in the same linked list.
The hash table that uses the chain address method to solve the conflict can be understood as the combination of array and linked list. In the above figure, an array with a length of 26 is used to store the initials, and each element of the array can be regarded as a single linked list. The data field of the linked list stores the names, and the pointer field points to the next node that stores the names with the same initials.
Dictionary design
Above, we have a general understanding of the hash table. Next, we design and implement a dictionary (dict). In this dictionary, we can store key value pairs or obtain the corresponding value (val) according to the key.
- Basic idea: the chain address method is adopted to represent the dictionary in the form of fixed length array + single chain table. Assuming that the array length is SIZE, the hash table in the initialization state is an array with all elements of 0.
- Stored key value pair: given a key value pair (key1, val1), the hash value (hash_code) is calculated by the hash function f, that is, hash_code1 = F(key1). Then, through hash_ Code1% size gets the address (because it is in the array, it is represented by Array[index] here). The modulo operation is to ensure that the address is within the range of the array address. Next, create a single linked list node (node 1), the pointer field next is NULL, and the data field stores key1 and val1. Finally, store the pointer to node 1 in Array[index].
- Conflict: given a key value pair (key2, val2), key2 ≠ key1, if calculated through the hash function, hash_code2 = hash_code1, the same address Array[index] will be obtained. At this time, there is a conflict because the pointer to node 1 has been stored in this position of the array.
- Conflict resolution: create a new single linked list node (node 2), save key2 and val2 in the data field, and NULL in the pointer field next. Let the next pointer of node 1 point to node 2 to solve the conflict, which is the chain address method, also known as the zipper method. Continue to use this method to solve the subsequent conflicts.
- Update operation: we inserted key value pairs (key1, val1) earlier. If we need to insert new key value pairs (key1, val0) on this basis, where val0 ≠ val1, we need to update. There are two methods. The first is to directly take the node of this key value as the first node in the corresponding position of the array. The second is to find the node with key=key1 in the corresponding position of the array, and then update its Val pointer.
- Look up dictionary: given a key, look up val. First, calculate the address array [index] = f (key)% size. If there is data, this address will store a pointer to the single linked list node, and then compare whether the data field key of the node pointed to by the pointer is equal to the key to be found. Ideally, it is equal, but due to the existence of conflict, it may be necessary to look down along the next pointer of the node. Therefore, the time complexity of the hash algorithm is not O(1). After finding the data, you can return. If there is no data, Array[index]=0 and NULL is returned.
Dictionary representation
/* Dictionary type */
#define DICT_TYPE_INT 0
#define DICT_TYPE_STR 1
typedef struct dict_entry {
/* Successor node */
struct dict_entry *next;
/* key */
void *key;
/* value */
void *val;
}dict_entry;
typedef struct dict {
/* hash function */
unsigned int (*hash)(void *key);
/* table Array is used to store dict_entry pointer */
dict_entry **table;
/* table Length of array */
int size;
/* Mask (size-1) */
int sizemask;
}dict;First look at dict_ The entry structure has three members, which are respectively used to represent the next pointer, key and value of the subsequent node, and to represent the node of the single linked list.
Then there is the dict structure, which is used to represent the dictionary itself.
- *Hash: for different types of keys, such as integer or character array (string), different hash functions need to be used. This member is a pointer function and points to the hash function of the dictionary.
- Table: note that the member table is an array used to store dict_ Pointer of type entry. You can use dict_entry* table[size] to assist understanding.
- size: the length of the table array.
- Sizemask: mask used to calculate the array index by and operation. Usually sizemask = size-1. Given a number x, X% size is equivalent to X & sizemask. And operation may be faster than modulo operation, so choose the former.

Function list
The following is the name of the function used to operate the queue and its function and complexity
| function | effect | Algorithm complexity |
|---|---|---|
| hash_integer | Calculates the hash value of an integer key | O(1) |
| hash_33 | Calculate the hash value of character key | O(N) |
| dict_create | Create a new dictionary | O(1) |
| dict_create_entry | Create a dict_entry | O(1) |
| dict_put_entry | Insert an entry into the dictionary | O(1) |
| dict_get_value | Get the val corresponding to the key | Best O(1), worst O(N) |
| dict_empty | Clear all entries in the dictionary | O(N2) |
| dict_release | Release entire dictionary | O(N2) |
Selection of hash function
/* Hash function (for integers) */
static unsigned int hash_integer(void *key)
{
return (*(int *)key * 2654435769) >> 28;
}
/* Hash function TIME33 algorithm (applicable to string)*/
static unsigned int hash_33(void *key)
{
unsigned int hash = 0;
while (*(char *)key != 0)
{
/* Shifting 5 bits to the left is equivalent to * 32, and then + hash is equivalent to * 33; */
hash = (hash << 5) + hash + *(char *)key++;
}
return hash;
}Hash function is a mapping relationship. Constructing hash function is a mathematical problem and there are many methods. In general, conflicts should be minimized and addresses should be evenly distributed as much as possible.
Here we choose a simple function to calculate the integer hash value and the TIME33 algorithm to calculate the string hash.
Expansion, there is a kind called MurmurHash The algorithm is widely known for being applied by Redis. It was invented by Austin Appleby in 2008. The inventor was invited to work at google.
Creation of hash table
/* Create a dict */
dict *dict_create(int type)
{
dict *dict = (struct dict *)malloc(sizeof(struct dict));
if(dict == NULL) return NULL;
if(type == DICT_TYPE_INT)
dict->hash = &hash_integer;
else
dict->hash = &hash_33;
dict->size = 1024;
dict->sizemask = dict->size - 1;
/* Request memory for array */
dict->table = (dict_entry **)malloc(sizeof(dict_entry *) *(dict->size));
if (dict->table == NULL) return NULL;
/* Set all array elements to zero */
memset(dict->table, 0, sizeof(dict_entry *) * (dict->size));
return dict;
}The function accepts a parameter type, which is used to determine the type of the dictionary below, so as to determine the corresponding hash function.
Then set the size of the dictionary and apply for memory for the table array. Then set all elements of the table to 0, which means that the position of the array is empty.
Finally, the new dictionary is returned.
Create dict_entry
/* Create a dict_entry */
dict_entry * dict_create_entry(void *key, void *val)
{
dict_entry * entry = (dict_entry *)malloc(sizeof(dict_entry));
if(entry == NULL) return NULL;
entry->key = key;
entry->val = val;
entry->next = NULL;
return entry;
}Create a dict_entry, that is, the node of the single linked list. Here, two void type pointers are accepted as parameters, so that the dictionary can store all kinds of data.
Dictionary insert key value pair
The first method:
/* Insert a key value pair into the dictionary */
dict *dict_put_entry(dict *dict, void *key, void *val)
{
unsigned int hash = dict->hash(key);
int pos = hash & dict->sizemask;
dict_entry *entry;
entry = dict_create_entry(key, val);
entry->next = dict->table[pos];
dict->table[pos] = entry;
return dict;
}This method is simple and effective. No matter adding, conflicting or updating operations, the new node generated by the key value pair to be inserted is the first node of the corresponding array position.
The essence of new addition and conflict is linked list insertion. When using this method, the update is not the actual update.
Since the new node is the first node corresponding to the array position, the old data (nodes with the same key) is arranged after the new node. When querying, the query starts from the first node of the linked list corresponding to the array position, so the new key value pair is always found first.
Advantages and disadvantages:
- It has the advantages of simple and elegant operation and high insertion efficiency. There is no need to traverse the linked list and calculate the hash value of each node key.
- The disadvantage is that the old nodes are still stored in the linked list, so they occupy more memory.
It is worth mentioning that Redis dcit uses this method when inserting key value pairs.
The second method:
/* Insert a key value pair into the dictionary */
dict *dict_put_entry(dict *dict, void *key, void *val)
{
unsigned int hash = dict->hash(key);
int pos = hash & dict->sizemask;
dict_entry *entry, *curr;
/* newly added */
if(dict->table[pos]==0){
printf("newly added\n");
entry = dict_create_entry(key, val);
dict->table[pos] = entry;
} else {
curr = dict->table[pos];
/* First, judge whether the first node meets the update condition */
if(dict->hash(curr->key) == dict->hash(key)) {
printf("to update\n");
curr->val = val;
return dict;
}
/* If not, look down until you find a node with a key with the same hash value, and update it,
* Or until next==NULL, it will be added at the end of the linked list. */
while(curr->next != NULL) {
printf("Look down\n");
if(dict->hash(curr->next->key) == dict->hash(key)) {
printf("to update\n");
curr->next->val = val;
return dict;
};
curr = curr->next;
}
printf("Tail insertion\n");
entry = dict_create_entry(key, val);
curr->next = entry;
}
return dict;
}This method can refer to the dictionary design mentioned above. The advantage is that it uses less memory, but the disadvantage is that it is not elegant enough and increases the complexity of the algorithm.
During debugging and testing, you can set dict - > size to 1 to observe additions, updates, conflicts, etc.
consult a dictionary
/* dict Get value */
void * dict_get_value(dict *dict, void *key)
{
unsigned int hash = dict->hash(key);
int pos = hash & dict->sizemask;
if(dict->table[pos]==0) return NULL;
dict_entry *current = dict->table[pos];
while (current)
{
if(dict->hash(current->key) == dict->hash(key))
return current->val;
else
current = current->next;
}
return NULL;
}Looking up the dictionary is to give a key and look up the corresponding val.
Refer to the design of the dictionary mentioned above.
Clearing and releasing dictionary
/* Clear all entries of dict without clearing dict itself */
void dict_empty(dict *dict)
{
int i;
for(i=0;i<dict->size;i++){
if(dict->table[i] != 0){
dict_entry * current, *next;
current = dict->table[i];
while (current)
{
next = current->next;
free(current);
current = next;
}
dict->table[i] = 0;
}
}
}
/* Release dict */
void dict_release(dict *dict)
{
dict_empty(dict);
free(dict->table);
free(dict);
}When clearing all entries of dict without clearing dict itself, you only need to traverse the table array. When you find elements that are not 0, you can traverse and clear the corresponding linked list.
To release dict, you only need to release all entries and then release dict itself.
Test in main function
int main()
{
/* Create a dictionary whose key is string type */
dict * dict = dict_create(1);
char str[] = "name";
char str2[] = "Austin";
char str3[] = "Lookcos";
char str4[] = "age";
int age = 18;
/* Key value pair: ("Austin", "Austin") */
dict_put_entry(dict, &str2, &str2);
puts(dict_get_value(dict, &str2));
/* Key value pair: ("name", "Austin") */
dict_put_entry(dict, &str, &str2);
puts(dict_get_value(dict, &str));
/* Key value pair: ("name", "Lookcos") */
dict_put_entry(dict, &str, &str3);
puts(dict_get_value(dict, &str));
/* Key value pair: ("age", 18) */
dict_put_entry(dict, &str4, &age);
printf("age: %d\n", *(int *)dict_get_value(dict, &str4));
/* Dictionary release */
dict_empty(dict);
dict_release(dict);
return 0;
}During the test, I use the second method for inserting key values. In addition, I set the size in dict to 1, so that there is a position in the table, which is convenient to observe the changes of the linked list during insertion, update and conflict.
Compile output
# gcc -fsanitize=address -fno-omit-frame-pointer -g dict.c && ./a.out newly added Austin Tail insertion Austin Look down to update Lookcos Look down Tail insertion age: 18
Complete code
This article is from my Github project: data structure (C language description)
https://github.com/LookCos/learn-data-structures