Author: bixia1994[1]

Reference link:

1. EIP721 implementation of Openzeppelin [2]
2. Azuki's EIP721A implementation [3]

Disadvantages of OpenZepplin implementation

In a typical NFT, the EIP721 template of OZ is usually used to realize the following:

function mintNFT(uint256 numberOfNfts) public payable {
    //Check that totalsupply cannot exceed
    require(totalSupply() < MAX_NFT_SUPPLY);
    require(numberOfNfts.add(totalSupply()) < MAX_NFT_SUPPLY);
    //Check numberOfNFT in (0,20]
    require(numberOfNfts > 0 && numberOfNfts <=20);
    //Check price * numberofnft = = MSG value
    require(numberOfNfts.mul(getNFTPrice()) == msg.value);
    //Execute the for loop. In each loop, mint is triggered once and a global variable is written
    for (uint i = 0; i < numberOfNfts; i++) {
     uint index = totalSupply();
     _safeMint(msg.sender, index);
    }
}

Among them_ safeMint is the mint API function provided in OZ, and its specific calls are as follows:

function _safeMint(
        address to,
        uint256 tokenId,
        bytes memory _data
    ) internal virtual {
        _mint(to, tokenId);
        require(
            _checkOnERC721Received(address(0), to, tokenId, _data),
            "ERC721: transfer to non ERC721Receiver implementer"
        );
    }
function _mint(address to, uint256 tokenId) internal virtual {
        require(to != address(0), "ERC721: mint to the zero address");
        require(!_exists(tokenId), "ERC721: token already minted");

        _beforeTokenTransfer(address(0), to, tokenId);

        _balances[to] += 1;
        _owners[tokenId] = to;

        emit Transfer(address(0), to, tokenId);

        _afterTokenTransfer(address(0), to, tokenId);
    }

From the above implementation process, we can see that for the ordinary NFT mint process, the algorithm complexity is O(N), that is, if the user needs to mint N NFTs, he needs to call the separate Mint method N times.

The core part is that in the implementation of OZ, two global mapping methods are maintained inside the mint method.

They are the balance used to record the number of NFTs owned by the user and the owners mapped from the tokenID to the user. Both mint and transfer need to update these two global variables internally. In terms of mint alone, one NFT requires at least two SSTORE. mint N NFTs require at least 2N SSTORE.

Improvement of ERC721A

From the implementation of Openzeppelin, the main disadvantage is that it does not provide batch Mint API, which makes the algorithm complexity reach O(N) when users batch mint Therefore, ERC721A proposes a batch Mint API, which reduces the algorithm complexity to O(1)

The simplest idea:

The simplest idea is to modify it directly_ The mint function also passes in the quantity of batch Mint as a parameter, and then_ Modify the two global variables balance and owners in the mint function. Because it is a batch mint, unlike OZ's separate Mint method, it needs to maintain a globally increasing tokenID inside the mint function. Another thing to note is that according to EIP721 specification, when the ownership of any NFT changes, a Transfer event needs to be issued. Therefore, it is also necessary to issue Transfer events in batches through the For loop.

function _mint(address to, uint256 quantity) internal virtual {
...//checks
        uint256 tokenId = _currIndex;
        _balances[to] += quantity;
        _owners[tokenId] = to;
···//emit Event
        for (uint256 i = 0; i < quantity; i++) {
           emit Transfer(address(0),to,tokenId);
           tokenId++;
        }
   //update index
        _currIndex = tokenId;
}

Analysis of this simple idea:

1. Is it O(1) or O(N)? The New mint must be O(1) algorithm complexity. It is easy to misunderstand that it still contains a for loop, but the for loop only operates on the emit event. From the perspective of OPCODE, in the for loop, there are only two opcodes, LOG4 and ADD, and there is no special consumption of Gas SSTORE. (tokenId + + is only a local variable + +, not a global variable + +, and the corresponding OPCODE is only ADD without SSTORE)
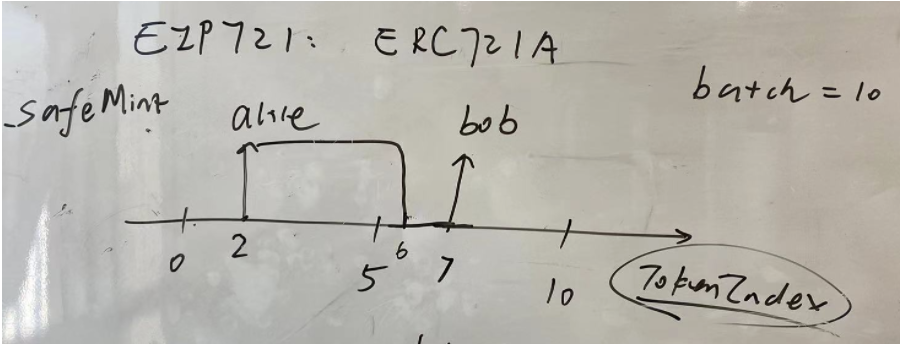
2. In the above Mint implementation, in fact, the ownership of the corresponding tokenId is only updated at the beginning of the user mint. In fact, the ownership of the corresponding tokenId is not updated for the subsequent tokenId, that is, it is still address(0) As shown in the following figure: after 5 minutes of alice, the system actually records its name only where tokenId=2_ owners[2]=alice, and other tokenids, such as 3, 4, 5 and 6. In order to save the number of SSTORE, the_ The owners are still address(0)=alice, and the other tokenids are 3, 4, 5 and 6. In order to save the number of SSTORE, its_ Owners is still address(0)! [") when the next user Bob comes to batch mint, he will start Mint directly from 7.

20220211151047.png

The question for this simplest idea:

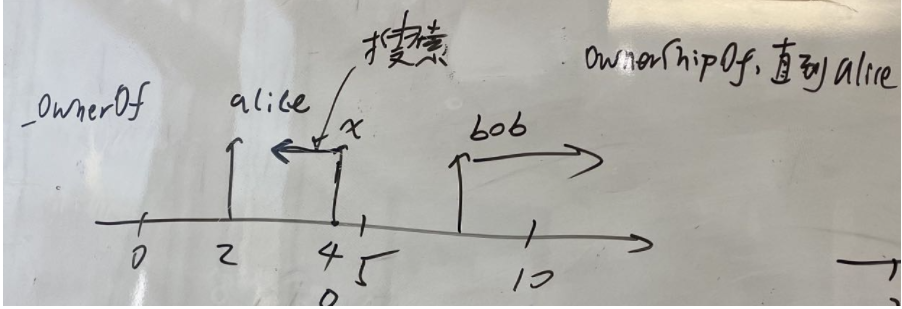
1. Because not every tokenid records the corresponding owner, who should be the owner of the tokenid with owners[tokenId]=address(0)? If it is the implementation of OZ, each tokenid has a corresponding owner address in owners[tokenId]. If it is address(0), it means that the tokenid has not been mint, that is_ exists[tokenId]=false. However, for ERC721A algorithm, there are two possible cases when the owners of a tokenid is address(0): 1 The tokenid does not Mint yet exist; 2. The tokenid belongs to an owner, but it is not the first in the owner's batch mint. That is, how to implement the ownerOf method: observe the tokenid obtained by mint, and you can find that it is a continuous and monotonically increasing integer sequence, i.e. 0,1,2,3 Considering only mint and not transfer, we can get a simple algorithm, that is, decreasing the tokenid in turn, and the first address that is not address(0) is the owner of the tokenid. How does the algorithm exclude the part of tokenid that has not been Mint out? You can compare the tokenid with the current currIndex. If tokenid < currIndex, it means that the owner of the tokenid must not be address(0). If tokenid > = currIndex, it means that the tokenid has not been mint.

20220211151107.png

function _exists(uint256 tokenId) internal view returns (bool) {
   tokenId < _currentIndex;
}

function ownershipOf(uint256 tokenId) internal view returns (TokenOwnership memory) {
//check exists
   require(_exists(tokenId),"OwnerQueryForNonexistentToken");
//Ergodic decrement
   for (uint256 curr = tokenId;curr >= 0;curr--) {
      address owner = _owners[curr];
      if (owner != address(0)) {
         return owner;
      }
   }
   revert("Ownership Error");
}
function ownerOf(uint256 _tokenId) external view returns (address) {
  return ownershipOf(_tokenId).addr;
}

1. If the user alice transfers to bob After mint, the tokenId area of alice will be discontinuous. How should I update it? That is, how to design the transfer method For alice, it has five NFTs: 2, 3, 4, 5 and 6. When it transfers 3 to bob, the system update should be as follows: first update bob to the owner of NFT with tokenId=3, and then update the owner of NFT with tokenId=4 from the original address(0) to alice. Transfer here is not a batch operation, but a single NFT operation. For batch transfer of multiple NFTs, this algorithm still needs O(N)

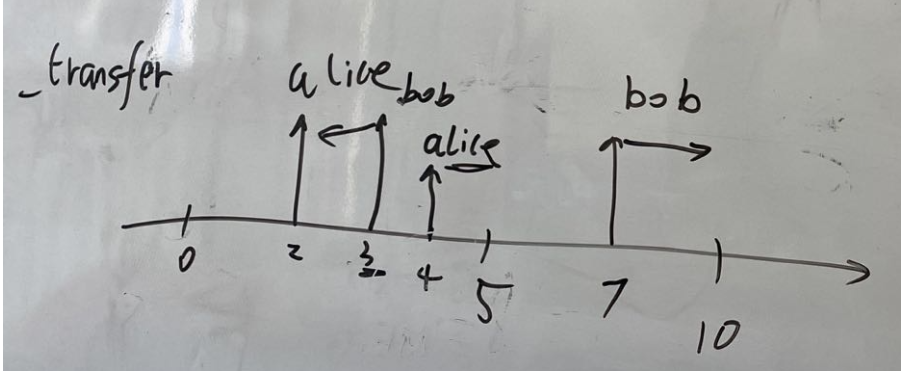
The specific implementation logic is as follows:

function _transfer(address from,address to,uint256 tokenId) private {
   //check ownership
   TokenOwnership memory prevOwnership = ownershipOf(tokenId);
   require(from == prevOwnership.addr);
   //update from&to
   balance[from] -= 1;
   balance[to] += 1;
   _owners[tokenId] = to;
   uint256 nextTokenId = tokenId + 1;
   if (_owners[nextTokenId] == address(0) && _exists(nextTokenId)) {
      _owners[nextTokenId] = from;
   }
   emit Transfer(from,to,tokenId);
}

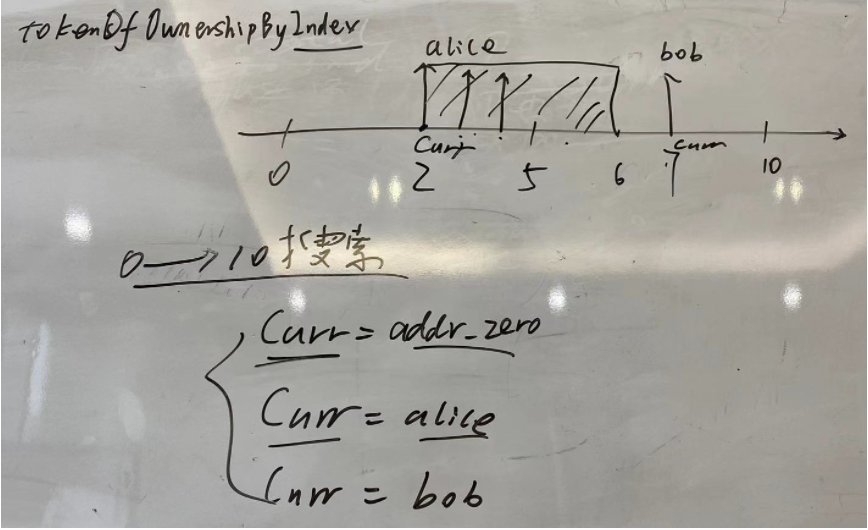
1. The third question is how to implement tokenOfOwnerByIndex, an enumeration method? In OZ, its implementation is based on a global mapping: mapping (address = > mapping (uint256 = > uint256)) private_ ownedTokens; However, in ERC721A, a corresponding owner is not stored for each tokenId. Naturally, it is impossible to obtain the tokenId list of an owner in this way. In view of the special problem solved by ERC721A, that is, all tokenids are continuous integers. The simplest idea is to traverse the entire tokenId sequence, find all tokenids belonging to the owner, and sort all tokenids according to the order of time stamps. For the same time stamp, it should be sorted according to the order of tokenId from small to large. According to EIP721 standard, there are no corresponding requirements for its sequence. Therefore, the above sorting method can not be used. Just keep it in order. The specific traversal process should be as follows: start traversing from tokenId=0, get the owner of the current tokenId and record it as curr. If the owner of the next tokenId is address(0), curr remains unchanged; If the owner of the next tokenId is not address(0), curr will be updated accordingly. If curr==alice, then tokensIdsIndex==index; if not, then tokensIdsIndex + + If equal, tokenId will be returned directly.

20220211151200.png

function tokenOfOwnerByIndex(address owner, uint256 index) public view override returns (uint256) {
    //check index <= balance
    require(index <= balanceOf(owner),"OwnerIndexOutOfBounds");
    uint256 max = totalSupply();
    uint256 tokenIdsIndex;
    uint256 curr;
    for (uint256 i = 0; i < max; i++) {
       address alice = _ownes[i];
       if (owner != address(0)) {
          curr = alice;
       }
       if (curr == owner) {
          if (index == tokenIdsIndex) return i;
          tokenIdsIndex++;
       }
    }
    revert("error");

}

Limitations of ERC721A algorithm

From the above analysis, it can be seen that ERC721A algorithm has a great breakthrough compared with the EIP721 implementation of Openzeppelin, but it also has its own limitations. There are still some parts I haven't understood clearly:

limitations:

ERC721A aims at the NFT batch casting process, which requires tokenId to increase continuously and monotonically from 0. If tokenId is a discontinuous positive integer, such as using timestamp as tokenId, the algorithm will actually fail.

Incomprehensible part:

Why do I need a timestamp?

struct TokenOwnership {
        address addr;
        uint64 startTimestamp;
    }

What's the use of this startTimestamp?

reference material

[1]

bixia1994: https://learnblockchain.cn/people/3295

[2]

EIP721 implementation of Openzeppelin: https://learnblockchain.cn/article/3041

[3]

Azuki's EIP721A implementation: https://www.azuki.com/erc721a