HashMap
Overview of HashMap
HashMap is an implementation of Map interface based on hash table. This implementation provides all optional mapping operations and allows null values and null keys to be used. (The HashMap class is roughly the same as Hashtable except for asynchronization and null enablement.) This kind of mapping does not guarantee the order of mapping, especially that it does not guarantee that the order will remain unchanged.
public class HashMap<K,V> extends AbstractMap<K,V> implements Map<K,V>, Cloneable, Serializable
It is worth noting that HashMap is not thread-safe. If you want a thread-safe HashMap, you can get a thread-safe HashMap through the static method synchronized Map of the Collections class.
Map map = Collections.synchronizedMap(new HashMap());
Data structure of HashMap
The bottom layer of HashMap is mainly based on arrays and linked lists. The reason why HashMap has a fairly fast query speed is that it determines the location of storage by calculating hash codes. HashMap calculates hash value mainly through hashCode of key, as long as hashCode is the same, the hash value calculated is the same. If there are too many stored objects, it is possible that different objects compute the same hash value, which leads to the so-called hash conflict. Students who have studied data structure know that there are many ways to solve hash conflicts. The bottom of HashMap is to solve hash conflicts through linked lists.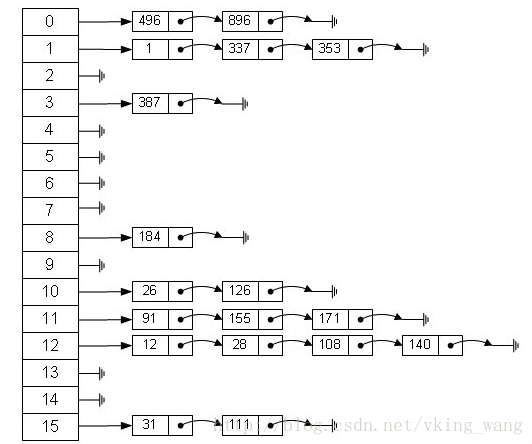
In the figure, the 0-15 part represents the hash table, also known as the hash array. Each element of the array is the head node of a single linked list. The list is used to resolve conflicts. If different key s are mapped to the same location of the array, they are put into the single linked list.
From the figure above, we can see that the hash table is composed of arrays + linked lists. In an array of 16 lengths, each element stores a Bucket bucket of the head node of the linked list. So what rules do these elements follow to store them in arrays? Generally, it is obtained by hash(key)%len, that is, the hash value of the key of the element is modular to the length of the array. For example, in the above hash table, 12% 16 = 12, 28% 16 = 12, 108% 16 = 12, 140% 16 = 12. So 12, 28, 108 and 140 are stored in the position of the array subscript 12.
HashMap is also implemented as a linear array, so it can be understood that its container for storing data is a linear array. This may make us wonder how a linear array can implement key-value pairs to access data. Here HashMap does some work.
First, we implement a static inner class Entry in HashMap. Its important attributes are key,value, next. From the attributes key and value, we can clearly see that Entry is a basic bean of HashMap key-value pair. We mentioned above that the foundation of HashMap is a linear array, which is Entry [], in Map. The contents of the surface are stored in Entry [].
Let's look at the Entry class code in HashMap:
/** Entry It's a one-way list.
* It is a linked list corresponding to "HashMap chain storage method".
* It implements the Map.Entry interface, which implements getKey(), getValue(), setValue(V value), equals(Object o), hashCode().
**/
static class Entry<K,V> implements Map.Entry<K,V> {
final K key;
V value;
// Point to the next node
Entry<K,V> next;
final int hash;
// Constructor.
// Input parameters include "hash value (h)", "key (k)", "value (v)", and "next node (n)".
Entry(int h, K k, V v, Entry<K,V> n) {
value = v;
next = n;
key = k;
hash = h;
}
public final K getKey() {
return key;
}
public final V getValue() {
return value;
}
public final V setValue(V newValue) {
V oldValue = value;
value = newValue;
return oldValue;
}
// Determine whether two Entries are equal
// If both Entry's "key" and "value" are equal, return true.
// Otherwise, return false
public final boolean equals(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry e = (Map.Entry)o;
Object k1 = getKey();
Object k2 = e.getKey();
if (k1 == k2 || (k1 != null && k1.equals(k2))) {
Object v1 = getValue();
Object v2 = e.getValue();
if (v1 == v2 || (v1 != null && v1.equals(v2)))
return true;
}
return false;
}
// Implementing hashCode()
public final int hashCode() {
return (key==null ? 0 : key.hashCode()) ^
(value==null ? 0 : value.hashCode());
}
public final String toString() {
return getKey() + "=" + getValue();
}
// When adding elements to HashMap, the drawing calls recordAccess().
// There's nothing to do here.
void recordAccess(HashMap<K,V> m) {
}
// When deleting elements from HashMap, the drawing calls recordRemoval().
// There's nothing to do here.
void recordRemoval(HashMap<K,V> m) {
}
}
HashMap is actually an Entry array. Entry objects contain keys and values. next is also an Entry object, which is used to handle hash conflicts and form a linked list.
Key attributes
First look at some key attributes in the HashMap class:
transient Entry[] table; //An array of entities that store elements transient int size; //Number of elements stored int threshold; //When the actual size exceeds the critical value, the capacity will be expanded. threshold = load factor*capacity final float loadFactor; //Loading factor transient int modCount; //Number of modifications
The loadFactor loading factor is the degree to which elements in the Hsah table are filled.
If: the larger the loading factor, the more elements filled, the advantage is that the space utilization rate is higher, but: the chance of conflict is increased, the length of the list will be longer and the search efficiency will be reduced.
Conversely, the smaller the load factor, the fewer elements to fill. The advantage is that the chance of conflict is reduced, but the space is wasted too much, and the data in the table will be too sparse (a lot of space is unused, and it begins to expand).
The greater the chance of conflict, the higher the cost of finding.
Therefore, we must find a balance and compromise between "conflict opportunities" and "space utilization". This kind of balance and compromise is essentially the balance and compromise of the famous "time-space" contradiction in data structure.
If the machine memory is enough and you want to improve the query speed, you can set the load factor a little smaller; on the contrary, if the machine memory is tight and there is no requirement for the query speed, you can set the load factor a little larger. But generally we do not need to set it, let it take the default value of 0.75.
Construction method
public HashMap(int initialCapacity, float loadFactor) {
// Ensuring digital legitimacy
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
// Find a power of 2 >= initialCapacity
int capacity = 1;
while (capacity < initialCapacity) // Ensure that the capacity is the n power of 2, so that the capacity is the n power of the smallest 2 that is greater than the initial Capacity
capacity <<= 1;
this.loadFactor = loadFactor;
threshold = (int)(capacity * loadFactor);
table = new Entry[capacity];
init();
}
public HashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
public HashMap() {
this.loadFactor = DEFAULT_LOAD_FACTOR;
threshold = (int)(DEFAULT_INITIAL_CAPACITY * DEFAULT_LOAD_FACTOR);
table = new Entry[DEFAULT_INITIAL_CAPACITY];
init();
}
We can see that when we construct HashMap, if we specify the load factor and initial capacity, we call the first constructor, otherwise we use the default. The default initial capacity is 16 and the default load factor is 0.75. We can see lines 13-15 in the above code. The function of this code is to ensure that the capacity is n-power of 2, so that the capacity is n-power of the smallest 2 than the initial Capacity. We'll see later why we set the capacity to n-power of 2.
Focus on the two most frequently used methods put and get in HashMap
Storage of data
Let's look at how HashMap stores data. First, let's look at HashMap's put method.
public V put(K key, V value) {
// If "key is null", the key-value pair is added to table[0].
if (key == null)
return putForNullKey(value);
// If "key is not null", the hash value of the key is calculated and added to the list corresponding to the hash value.
int hash = hash(key.hashCode());
// Search for the index of the specified hash value in the corresponding table
int i = indexFor(hash, table.length);
// Loop through the Entry array and replace the old value with a new value if the key pair already exists. Then quit!
for (Entry<K,V> e = table[i]; e != null; e = e.next) {
Object k;
if (e.hash == hash && ((k = e.key) == key || key.equals(k))) { //If the key is the same, override and return the old value
V oldValue = e.value;
e.value = value;
e.recordAccess(this);
return oldValue;
}
}
//Number of modifications + 1
modCount++;
//Add key-value to table[i]
addEntry(hash, key, value, i);
return null;
}
An important internal interface is used in the above program: Map.Entry. Each Map.Entry is actually a key-value pair. As can be seen from the above program, when the system decides to store key-value pairs in HashMap, it does not consider the value in Entry at all, but only calculates and determines the storage location of each Entry based on the key. This also illustrates the previous conclusion: we can absolutely regard the value in the Map set as the attachment of the key. When the system determines the storage location of the key, the value can be saved there.
Let's analyze this function slowly. Lines 2 and 3 deal with the case where the key value is null. Let's look at the putForNullKey(value) method:
private V putForNullKey(V value) {
for (Entry<K,V> e = table[0]; e != null; e = e.next) {
if (e.key == null) { //If an object whose key is null exists, it is overwritten.
V oldValue = e.value;
e.value = value;
e.recordAccess(this);
return oldValue;
}
}
modCount++;
addEntry(0, null, value, 0); //If the key is null, the hash value is 0
return null;
}
Note: If the key is null, the hash value is 0, and the object is stored in an array where the index is 0. That is table[0].
Let's go back to line 4 of the put method. It calculates the hash code by the hashCode value of the key. The following function calculates the hash code:
// The method of calculating hash values is calculated by hashCode of keys
final int hash(Object k) {
int h = 0;
if (useAltHashing) {
if (k instanceof String) {
return sun.misc.Hashing.stringHash32((String) k);
}
h = hashSeed;
}
h ^= k.hashCode();
// This function ensures that hashCodes that differ only by
// constant multiples at each bit position have a bounded
// number of collisions (approximately 8 at default load factor).
h ^= (h >>> 20) ^ (h >>> 12);
return h ^ (h >>> 7) ^ (h >>> 4);
}Having obtained the hash code, the index that should be stored in the array is calculated by hash code. The function of calculating the index is as follows:
static int indexFor(int h, int length) { //Calculate index values based on hash values and array length
return h & (length-1); //There is a reason why hash & (length-1) can't be reckoned freely here, so as to ensure that the calculated index is within the size of the array and will not exceed it.
}
We want to emphasize that it is natural for hash table hashing to think of using hash value to modularize length (i.e. division hash method), which is also implemented in Hashtable. This method can basically ensure that elements are hashed evenly in hash table, but modularization will use division operation, which is inefficient, HashMap. Meanwhile, the method of H & (length-1) is used to replace the mode taking, which also achieves uniform hashing, but the efficiency is much higher, which is also an improvement of Hashtable by HashMap.
Next, we analyze why the capacity of a hash table must be an integer power of 2. First, if length is an integer power of 2, H & (length-1) is equivalent to modularizing length, which ensures the uniformity of hash and improves efficiency. Secondly, if length is an integer power of 2, it is even, so that length-1 is odd and the last bit of odd number is 1, thus ensuring the last of H & (length-1). Bit may be 0 or 1 (depending on the value of h), i.e., the result after that may be even or odd, so as to ensure the uniformity of the hash. If length is odd, it is obvious that length-1 is even, and its last bit is 0, so the last one of H & (length-1) must be 0, that is, only 0. For an even number, any hash value will only be hashed to the even subscript position of the array, which wastes nearly half of the space. Therefore, length takes the integer power of 2 in order to reduce the probability of collisions between different hash values, so that elements can be hashed evenly in the hash table.
This seems very simple, but in fact, it is quite mysterious. Let's give an example to illustrate that:
Assuming that the array length is 15 and 16, and the optimized hash codes are 8 and 9, the results are as follows:
h & (table.length-1) hash table.length-1
& (15-1): 0100 & 1110 = 0100
& (15-1): 0101 & 1110 = 0100
-----------------------------------------------------------------------------------------------------------------------
& (16-1): 0100 & 1111 = 0100
& (16-1): 0101 & 1111 = 0101
As can be seen from the ex amp le above, when they are "and" with 15-1 (1110), they produce the same result, that is to say, they will be located in the same position in the array, which results in collision, 8 and 9 will be placed in the same position in the array to form a linked list, so the query needs to be traversed. This list, get 8 or 9, which reduces the efficiency of the query. At the same time, we can also find that when the length of the array is 15, the hash value will "and" with 15-1 (1110). Then the last one will always be 0, while 0001, 0011, 0101, 1001, 1011, 0111 and 1101 will never be able to store elements. The space waste is considerable. What's worse, in this case, arrays can never store elements. The location available is much smaller than the length of the array, which means further increasing the probability of collision and slowing down the efficiency of queries! When the length of the array is 16, that is to say, the n-th power of 2, the value of the number of bits of the binary number obtained by 2n-1 is 1, which makes the low position of the original hash the same, and the hash(int h) method is used to further optimize the hashCode of the key, adding the high bit calculation, so that only two values of the same hash value are obtained. It will be placed in the same place in the array to form a linked list.
So, when the length of the array is n power of 2, the probability of index calculated by different key s is smaller, so the distribution of data on the array is more uniform, that is to say, the probability of collision is small, relatively, when querying, there is no need to traverse the linked list at a certain location, so the query efficiency is higher.
According to the source code of the put method above, when a program attempts to put a key-value pair into a HashMap, the program first determines the storage location of the Entry based on the hashCode() return value of the key: if the hashCode() return value of two Entry keys is the same, then their storage location is the same. If the two Entry keys return true by comparing equals, the newly added value of Entry will override the value of the original Entry in the collection, but the key will not override it. If the two Entry keys return false by comparing equals, the newly added Entry will form an Entry chain with the original Entry in the collection, and the newly added Entry is located at the head of the Entry chain -- see the description of the addEntry() method.
void addEntry(int hash, K key, V value, int bucketIndex) {
Entry<K,V> e = table[bucketIndex]; //If the location to be added has a value, set the original value of the location to next of the new entry, which is the next node of the new entry list.
table[bucketIndex] = new Entry<>(hash, key, value, e);
if (size++ >= threshold) //If it is greater than the critical value, the capacity will be expanded.
resize(2 * table.length); //Expansion by 2 multiples
}
The parameter bucketIndex is the index value calculated by the indexFor function. The second line of code is to get the Entry object indexed by the bucketIndex in the array. The third line is to construct a new Entry object with hash, key and value and put it in the position indexed by the bucketIndex, and set the original object in the place to the next composition of the new object. Link list.
Lines 4 and 5 are to determine whether the size reaches the threshold after put ting. If it reaches the threshold, it needs to be expanded. HashMap's expansion is twice as large as the original.
Capacity expansion
The resize() method is as follows:
Resizing HashMap, new Capacity is the adjusted unit
void resize(int newCapacity) {
Entry[] oldTable = table;
int oldCapacity = oldTable.length;
if (oldCapacity == MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return;
}
Entry[] newTable = new Entry[newCapacity];
transfer(newTable);//All the elements used to move the original table into the new table
table = newTable; //Then assign the newTable to the table
threshold = (int)(newCapacity * loadFactor);//Recalculate the critical value
}
A new underlying array of HashMap is created. Behavior 10 in the above code calls transfer method, adds all elements of HashMap to the new HashMap, and recalculates the index position of elements in the new array.
void transfer(Entry[] newTable) {
int newCapacity = newTable.length;
for (Entry<K,V> e : table) {
while(null != e) {
Entry<K,V> next = e.next;
int i = indexFor(e.hash, newCapacity);
e.next = newTable[i];
newTable[i] = e;
e = next;
}
}
}
As the number of elements in HashMap increases, the probability of hash collision increases, because the length of the array is fixed. So in order to improve query efficiency, we need to expand HashMap's array. Array expansion will also appear in Array List. This is a common operation. After HashMap's array expansion, the most performance-consuming point appears: the data in the original array must be recalculated in the new array. And put it in. That's resize.
So when will HashMap expand? When the number of elements in HashMap exceeds the array size * loadFactor, the array is expanded. The default value of loadFactor is 0.75, which is a compromise. That is to say, by default, the array size is 16, so when the number of elements in HashMap exceeds 16 * 0.75 = 12, the size of the array is expanded to 2 * 16 = 32, that is to say, the size of the array is doubled, and then the position of each element in the array is recalculated. Expansion requires array replication. Replication of the array is very performance-consuming. Operation, so if we have predicted the number of elements in HashMap, the number of preset elements can effectively improve the performance of HashMap.
data fetch
public V get(Object key) {
if (key == null)
return getForNullKey();
int hash = hash(key.hashCode());
for (Entry<K,V> e = table[indexFor(hash, table.length)];
e != null;
e = e.next) {
Object k;
if (e.hash == hash && ((k = e.key) == key || key.equals(k)))
return e.value;
}
return null;
}
private V getForNullKey() {
if (size == 0) {
return null;
}
for (Entry<K,V> e = table[0]; e != null; e = e.next) {
if (e.key == null)
return e.value;
}
return null;
}
With the hash algorithm of the above storage as the basis, it's easy to understand this code. From the source code above, we can see that when get element in HashMap, we first calculate the hashCode of key, find an element of the corresponding position in the array, and then find the required element in the list of corresponding positions by the equals method of key.
To sum up, HashMap treats key-value as a whole at the bottom, which is an Entry object. HashMap uses an Entry [] array at the bottom to store all key-value pairs. When an Entry object needs to be stored, its storage location in the array will be determined by hash algorithm, and its storage location in the linked list at the array location will be determined by equals method. When an Entry is needed, it will also be rooted. The hash algorithm finds its storage location in the array, and then extracts the Entry from the list of the location according to the equals method.
Delete data
final Entry<K,V> removeEntryForKey(Object key) {
int hash = (key == null) ? 0 : hash(key);
int i = indexFor(hash, table.length);
Entry<K,V> prev = table[i];
Entry<K,V> e = prev;
while (e != null) {
Entry<K,V> next = e.next;
Object k;
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k)))) {
modCount++;
size--;
// Delete the header node of the linked list
if (prev == e)
table[i] = next;
else // Delete the non-header node of the linked list
prev.next = next;
e.recordRemoval(this);
return e;
}
prev = e; // The current node is set to the pre-node
e = next; // The next node is assigned to the cyclic variable e
}
return e;
}Performance parameters of HashMap
HashMap contains the following constructors:
HashMap(): Construct a HashMap with an initial capacity of 16 and a load factor of 0.75.
HashMap (int initial capacity): Construct a HashMap with initial capacity and load factor of 0.75.
HashMap (int initial capacity, float loadFactor): Creates a HashMap with the specified initial capacity and load factor.
HashMap's basic constructor, HashMap (int initial capacity, float loadFactor), has two parameters: initial capacity and load factor.
Initial Capacity: The maximum capacity of a HashMap, which is the length of the underlying array.
Load Factor: The load factor loadFactor is defined as the actual number of elements in the hash table (n) / the capacity of the hash table (m).
Load factor measures the degree of space usage of a hash table. The larger the load factor, the higher the loading degree of the hash table, and vice versa. For a hash table using linked list method, the average time to find an element is O(1+a), so if the load factor is larger, the space will be more fully utilized, but the result is that the search efficiency will be reduced; if the load factor is too small, the data of the hash table will be too sparse, causing serious waste of space.
In the implementation of HashMap, the maximum capacity of HashMap is determined by threshold field:
threshold = (int)(capacity * loadFactor);
Combining with the definition formula of load factor, threshold is the maximum number of elements allowed under the corresponding load factor and capacity. If it exceeds this number, it will be resized again to reduce the actual load factor. The default load factor of 0.75 is a balanced choice of space and time efficiency. When the capacity exceeds this maximum capacity, the resize HashMap has twice the capacity.
if (size++ >= threshold)
resize(2 * table.length);
Fail-Fast mechanism
We know that java.util.HashMap is not thread-safe, so if other threads modify the map in the process of using the iterator, the Concurrent ModificationException will be thrown, which is the so-called fail-fast strategy.
This strategy is implemented in the source code through the modCount field. modCount, as its name implies, is the number of modifications. Modifications to HashMap content will increase this value, which will be assigned to the expectedModCount of the iterator in the initialization process.
private abstract class HashIterator<E> implements Iterator<E> {
Entry<K,V> next; // next entry to return
int expectedModCount; // For fast-fail
int index; // current slot
Entry<K,V> current; // current entry
HashIterator() {
expectedModCount = modCount;
if (size > 0) { // advance to first entry
Entry[] t = table;
while (index < t.length && (next = t[index++]) == null)
;
}
}
public final boolean hasNext() {
return next != null;
}
final Entry<K,V> nextEntry() {
if (modCount != expectedModCount)
throw new ConcurrentModificationException();
Entry<K,V> e = next;
if (e == null)
throw new NoSuchElementException();
if ((next = e.next) == null) {
Entry[] t = table;
while (index < t.length && (next = t[index++]) == null)
;
}
current = e;
return e;
}
public void remove() {
if (current == null)
throw new IllegalStateException();
if (modCount != expectedModCount)
throw new ConcurrentModificationException();
Object k = current.key;
current = null;
HashMap.this.removeEntryForKey(k);
expectedModCount = modCount;
}
}
In the iteration process, determine whether modCount and expectedModCount are equal, if not equal, it means that other threads have modified Map:
Notice that modCount is declared volatile to ensure visibility of changes between threads.
final Entry<K,V> nextEntry() {
if (modCount != expectedModCount)
throw new ConcurrentModificationException();
}
In the API of HashMap, it is pointed out that:
The iterator returned by the "collection view method" of all HashMap classes fails quickly: after the iterator is created, if the mapping is structurally modified, the iterator will throw Concurrent ModificationE at any time and in any other way unless the iterator itself remove s the method. Xception. Therefore, in the face of concurrent modifications, iterators will soon fail completely without risking arbitrary uncertain behavior at uncertain times in the future.
Note that the fast failure behavior of iterators cannot be guaranteed. Generally speaking, it is impossible to make any firm guarantees in the presence of asynchronous concurrent modifications. Fast Failure Iterator tries its best to throw Concurrent ModificationException. Therefore, it is wrong to write programs that depend on this exception. The correct approach is that the iterator's fast failure behavior should only be used to detect program errors.