1. Greedy strategy:

The so-called greedy strategy is to make the best choice in the current situation at each step and get the global optimal solution by summing up the local optimal solutions. Of course, a topic may not be able to obtain a global optimal solution from a local optimal solution (a typical example is the shortest path problem), so the greedy strategy will not apply and other strategies (such as DP) should be chosen.

Solving greedy problems:

1. First determine whether the greedy strategy is met (global optimal solution can be obtained from local optimal solution)

2. Split the problem into subproblems to find a local optimal solution

3. Combine the answers of the sub-questions to get a global optimal solution

4. Greedy strategies always make the best choice at the moment, so summing up the operations to get the best value is combined. Most greedy problems tend to be sorted first (or use a priority queue).

2. Examples

There is no universal template for the topic of greedy algorithm. There is only one way to quickly make a greedy problem. Brush more questions. This topic is skilled when you have seen nature before, but there is no shortcut. Because of the limited space, bloggers can't give many examples for readers to train, so they need to rely on readers to actively search the network for greedy algorithm questions to practice. Here are just a few examples to give your readers an idea of greedy strategies.

 1. Homework

  Once when Gerald studied in the first year at school, his teacher gave the class the following homework. She offered the students a string consisting of n small Latin letters; the task was to learn the way the letters that the string contains are written. However, as Gerald is too lazy, he has no desire whatsoever to learn those letters. That's why he decided to lose some part of the string (not necessarily a connected part). The lost part can consist of any number of segments of any length, at any distance from each other. However, Gerald knows that if he loses more than k characters, it will be very suspicious.

  Find the least number of distinct characters that can remain in the string after no more than k characters are deleted. You also have to find any possible way to delete the characters.

General idea: Given a string and integer k, you can delete up to K characters. Ask the minimum number of types of characters in the deleted string, and output the string after the deleted characters. Example:

Input: aaaaa 4 Output: 1 aaaaa

Input: abacaba 4 Output: 1 aaaa

Input: abcdefgh 10 * Output: 0

Greedy ideas: Count the number of occurrences of each character in the string, and delete the fewer occurrences first.

#include<bits/stdc++.h>
using namespace std;
char str[100005];
struct Node{
	char flag;
	vector<int> num;
	int size=0;
};
bool compare(Node a,Node b){
	if(a.size==b.size) return a.flag<b.flag;//When the number is the same, delete the dictionary in smaller order first
	return a.size<b.size;
}
Node node[26];
int main(){
	int k;
	gets(str);
	cin>>k;
	int len=strlen(str);
	if(k>=len)	cout<<0<<"\n";//Allow deletion of characters beyond string length to print 0 directly
	else{
		for(int i=0;i<len;++i){
			node[str[i]-'a'].flag=str[i];//You do not need to save characters if you do not require a preferential deletion of small dictionary characters
			node[str[i]-'a'].num.push_back(i);
			node[str[i]-'a'].size++;
		}	
		sort(node,node+26,compare);//Sort characters from smallest to largest by number of occurrences, removing fewer characters first
		int total=0,rest=26;
		for(int i=0;i<26;++i){//A total of 26 characters, up to 26 operations
			int j=0;
			if(k-total>=node[i].size)//Stop when the number of characters allowed to be deleted is insufficient to reduce the number of characters
				for(;j<node[i].size;++j){
					str[node[i].num[j]]=0;//Set the character at this position to 0 to indicate that it has been deleted
					total++;//total represents the number of characters deleted
				}
			if(j==node[i].size) rest--;//When a character deletion is complete, the number of remaining characters is -1
		}
		printf("%d\n",rest);//Print remaining characters
		for(int i=0;i<len;++i)
			if(str[i]) printf("%c",str[i]);//Print deleted characters
	}
    return 0;
}

2. Coin combinations

General idea: Given a range of M and n coins with different currency values, the number of each coin is unlimited. Ask how many coins can cover all the values of 1~m at least (that is, any given value of 1~m can be combined from the selected coins). If the required output of -1 cannot be met:

Input: 114 * Output: 5

           1 2 5 10

Interpretation: Select one coin, two two coins, one five coins, and one ten coins. 1=1, 2=2, 3=2+1, 4=2+2, 5=5, 6=5+1, 7=5+2, 8=5+2+1, 9=5+2, 10=10, 11=10+1, all currency values of 1~m can be combined.

Greedy ideas: This topic is a more difficult greedy topic. If you want to make up all the coin values in the range of 1-m, you must first ask for a coin with one dollar. Otherwise, you cannot make up a coin with one dollar. Note that the number of coins is infinite. If you have a coin with one dollar, you can actually make up all the coin values in the range of 1-m without other coins. So the only unsuccessful situation is a coin without a dollar. You should also be aware that a currency greater than m has no contribution to the outcome, so only coins with a currency less than m are considered. Now assume the maximum value of a coin less than m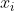And 1~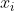The range of -1 has been compacted, so how do you choose the smallest coins if you want to compact 1~m? The answer is, of course, the larger the currency value you choose, the fewer coins you will use. The largest coin you have today is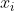So select all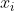Is the least choice! But how can you ensure that you can cover all currency values from 1 to m? Note this important precondition: 1~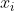The interval of -1 has been compacted! With this condition we can know that when we choose one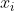When coins are used, the range covered by the currency value is 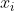1~-1+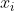That is, 1~2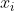-1 (must understand), choose 2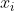When coins are used, they can cover an interval of 1-3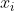-1, and so on, and so on, and so on, to cover m satisfies n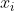-1=m, n=(m+1)/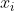To select n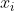Coins, then n coins are values ranging from 1 to 1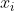Minimum coin selection for -1 to 1~m. Similarly, to get coverage 1~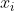Minimum coin selection for the -1 range, simply add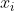-1 as m, find less than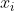The maximum currency value of -1 is then calculated to n, and the sum of the minimum coin selections for each interval is the total minimum number of coins required.

The following code was written by the blogger a long time ago and differs slightly from the inference above. Readers can refer to it and modify it themselves:

#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
int money[1005];
//The dichotomy looks for locations that are less than or equal to the currency value to be composed, because we don't need a larger coin
int binary(int l,int r,int x){
	int mid;
	while(l<r){
		mid=(l+r+1)>>1;
		if(money[mid]<=x)	l=mid;
		else r=mid-1;
	}
	return l;
}
int main(){
	int m,n;
	cin>>m>>n;
	for(int i=1;i<=n;++i)
		cin>>money[i];
	sort(money+1,money+n+1);//Let coins be sorted from smallest to largest first
    //Note that if there is no 1 in this stack of coins, it is impossible to make up a 1-m coin value, because a currency value of 1 can only be made up of 1-yuan coins, and with 1 it is bound to make up a 1-m coin value, at least not all 1 will do
	if(money[1]!=1)	cout<<"-1\n";
	else{
		int ans=0;
		int index=binary(1,n,m);
		int temp=ans,sum=0;
		for(int i=2;i<=index;++i){
            //As inferred above, money[i]-1 is not supposed to be money[i]-1 here, but because money[i] is the default here, readers can consider modifying it as they write code
			ans+=(money[i]-1)/money[i-1];
			sum+=(ans-temp)*money[i-1];//This sometimes covers not only the full range but also the larger range of the overflow range.
			temp=ans;
		}
        //Since it is possible that the previous coin covers a larger range, eliminating the last coin, you need to subtract the previous coin cover and perform an upward rounding.
		ans+=ceil((double)(m-sum)/money[index]);//Notice the mandatory transition here. Nothing can achieve the effect of rounding up.
		cout<<ans<<"\n";
	}
	return 0;
}

3.Pay off

Xiaodu has hired a new employee, Niu Niu, who needs to be paid at least m yuan monthly (the wage for Niu Niu can be equal to or greater than m yuan, not less than m). Xiaodu has some money with n different denominations. For denomination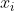Banknote, small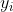i, and each bill's face value divides all larger face values, and each bill cannot find zero.
To a lesser extent, would you like to know how many months'wages this part of the fund can give cows and cattle?

Input: 351 * Output: 4

            100 1

             50 4

             1 2

The greedy way of thinking: Make sure that each selection wastes the least amount of money, that is, the closer you get to m, the better. In fact, when you can't compile m, you can use a small amount of money to make up for it first.

#include<cstdio>
#include<iostream>
#include<cstring> 
#include<algorithm>
#include<queue>
using namespace std;
const int N=100010;
struct Money{
    int x, y;
    bool operator < (const Money e) const{
        return x<e.x;
    }
} money[N];
int main() {
    ios::sync_with_stdio(false);
    int n,m;
    cin>>n>>m;
    for(int i=0;i<n;++i)
        cin>>money[i].x>>money[i].y;
    sort(money,money+n);//Sort money by currency value from smallest to largest
    int ans=0;
    while(1){
        int need,rest=m;
        //Firstly, try to compact m, then the waste is 0. This gives priority to large amounts of money because small amounts are used to make up for M
        for(int i=n-1;i>=0;--i){
            if(money[i].y==0) continue;
            need=rest/money[i].x;
            if(need>money[i].y) need=money[i].y;
            money[i].y-=need;
            rest-=need*money[i].x;
            if(rest==0) break;
        }
        //Can't compact m, give priority to small amount of money to make up for, such waste is the least
        if(rest!=0){
            for(int i=0;i<n;++i){
                if(money[i].y==0) continue;
                need=rest/money[i].x+1;//Add 1 to cover m's money
                if(need>money[i].y) need=money[i].y;
                money[i].y-=need;
                rest-=need*money[i].x;
                if(rest<=0) break;
            }
        }
        //Explain that the remaining money is not enough m, jump out of the cycle
        if(rest>0) break;
        ans++;
    }
    cout<<ans<<endl;
    return 0;
}