preface
For many caching middleware, memory is the main battlefield of its operation. For redis, redis is a necessary choice for many Internet companies. Redis has many characteristics of efficiency, simplicity and ease of use, and is widely used by everyone. However, we know that most redis operations belong to memory level operations. If they are used to store large quantities of data, with the growth of time, Performance is bound to decline. Therefore, in order to solve such problems, redis itself provides many policy configurations for eliminating cache;
The cache elimination strategy can effectively alleviate the problems of unknown space and performance degradation caused by tight memory during the operation of redis service. In addition, many similar middleware, such as spark, clickhouse and other middleware with memory as the main operation, have similar cache elimination mechanisms;
No matter how complex their elimination strategies are, the basic principles are similar. In the final analysis, the configuration of cache elimination strategies is based on a set of algorithms. Below, I will list several commonly used cache elimination strategy algorithms for reference and understanding;
1,FIFO
First come, first out; When mapping a data structure, that is, first in first out, it is easy to think that some data structures in Java have similar characteristics;
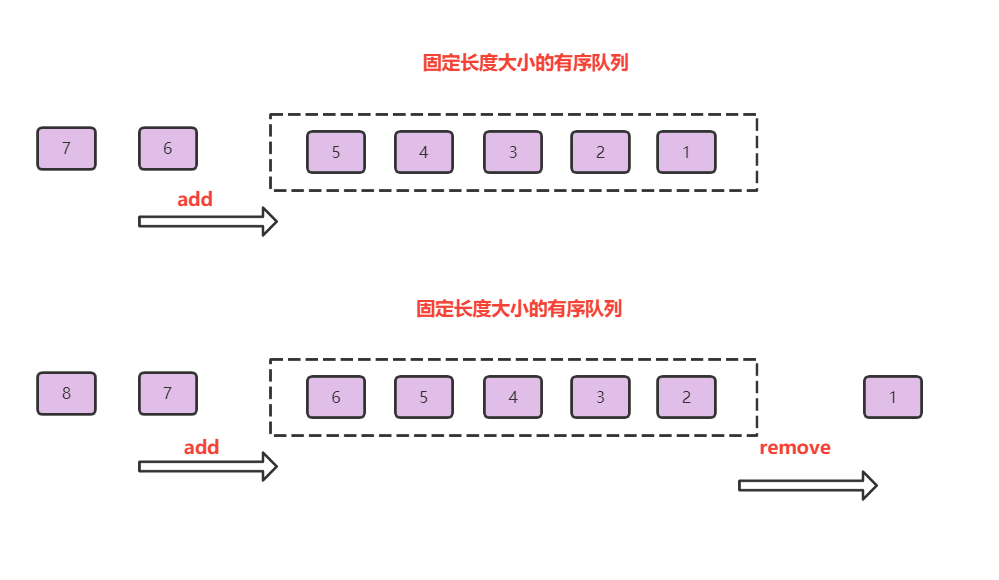
The working diagram of FIFO can refer to the above diagram, and its characteristics are briefly summarized as follows:
- An ordered queue of fixed length
- The elements in and out of the queue are arranged in order and can be located by subscript (index)
- When the queue length reaches the upper limit, remove one or more of the earliest queues in the queue
Therefore, it is easy for us to think that the linkedList in Java can be used. I believe that students with a little Java foundation can quickly roll out the following code
/**
* First in first out FIFO
*/
public class FiFo {
//As a queue for storing elements
static LinkedList<Integer> fifo = new LinkedList<Integer>();
//Defines the maximum length of the queue
static int QUEUE_SIZE = 3;
public static void main(String[] args) {
FiFo fifo = new FiFo();
System.out.println("begin add 1‐3:");
fifo.add(1); fifo.add(2); fifo.add(3);
System.out.println("begin add 4:");
fifo.add(4);
System.out.println("begin read 2:"); fifo.read(2);
System.out.println("begin read 100:"); fifo.read(100);
System.out.println("add 5:"); fifo.add(5);
}
public void add(int i) {
fifo.addFirst(i);
if (fifo.size() > QUEUE_SIZE) {
fifo.removeLast();
}
showData();
}
//Print queue data
public void showData() {
System.out.println(this.fifo);
}
/**
* Read queue data
* @param data
*/
public void read(int data) {
Iterator<Integer> iterator = fifo.iterator();
while (iterator.hasNext()) {
int j = iterator.next();
if (data == j) {
System.out.println("find the data");
showData();
return;
}
}
System.out.println("not found");
showData();
}
}
The program mainly provides three methods: join the queue, remove the earliest added element in the queue, and several methods to read the expected element in the queue. Run this code to deepen your experience through the contents of the printout

Summary:
- FIFO implementation is relatively simple
- The elimination strategy implemented by FIFO is rough, only considering from the time dimension, regardless of the use of elements, that is, even if it may be frequently used data, the earliest added data may be killed
- It is less used in actual production and is not humanized
2,LRU
The longest unused
The full name of LRU is Least Recently Used, that is, the value with the longest time of last use is eliminated. FIFO is very rough. Whether it is used or not, it directly kicks out the elements with a long time. LRU believes that the data that has been frequently used recently is likely to be frequently used in the future, so it will eliminate those lazy data.

The working principle of LRU algorithm can be understood according to the above figure, and its process is summarized as follows:
- For a fixed length queue, the incoming data is stored in the queue in order before reaching the maximum capacity
- If no data has been read, the incoming data will be eliminated according to the FIFO strategy (everyone is equal at this time)
- If any data in the middle has been read, the read data will move to the end of the queue (the same is true for other elements)
- The elements that re-enter the queue remove (eliminate) the elements at the head of the queue
The LRU algorithm takes into account the data reading (use) operation, which is also consistent with the above explanation, that is, the read elements are considered to have higher priority. LRU can be realized by using LinkedHashMap, array and linked list in Java. The following code can be directly described in combination with the comments,
/**
* Longest unused elimination [first in first out]
*/
public class LRU {
//As a queue for storing elements
static LinkedList<Integer> lru = new LinkedList<Integer>();
//Defines the maximum length of the queue
static int QUEUE_SIZ = 3;
//Add element
public void add(int i) {
lru.addFirst(i);
if (lru.size() > QUEUE_SIZ) {
lru.removeLast();
}
showData();
}
//Read data
public void read(int data) {
Iterator<Integer> iterator = lru.iterator();
int index = 0;
while (iterator.hasNext()) {
int temData = iterator.next();
if (data == temData) {
System.out.println("find the data");
//Once the element is found, remove the element at this location and move it to the end of the queue
lru.remove(index);
lru.addFirst(temData);
showData();
return;
}
index++;
}
System.out.println("not found!");
showData();
}
//print data
public void showData() {
System.out.println(this.lru);
}
public static void main(String[] args) {
LRU lru = new LRU();
System.out.println("begin add 1‐3:");
lru.add(1);
lru.add(2);
lru.add(3);
System.out.println("add 4:");
lru.add(4);
System.out.println("read 2:");
lru.read(2);
System.out.println("read 5:");
lru.read(5);
System.out.println("add 5:");
lru.add(5);
}
}
The most critical part is in the data reading method, which can be understood by referring to the notes. Next, run this code to deepen the understanding through the console output,

Summary:
- Compared with FIFO, it increases the judgment according to the used dimension, which is more suitable for rational selection
- The dimension of judgment is not sufficient, only considering the time of use, without considering more factors such as frequency of use
3,LFU
Least recently used
Least Frequently Used. It wants to eliminate the elements that have been used the least times in the recent period of time. It can be considered as more judgment than LRU.
LFU needs time and times for reference. It should be noted that the two dimensions may involve the same access times in the same time period, so a counter and a queue must be built in. The counter counts the number of access elements, and the queue is used to place the access time when the same count is placed.
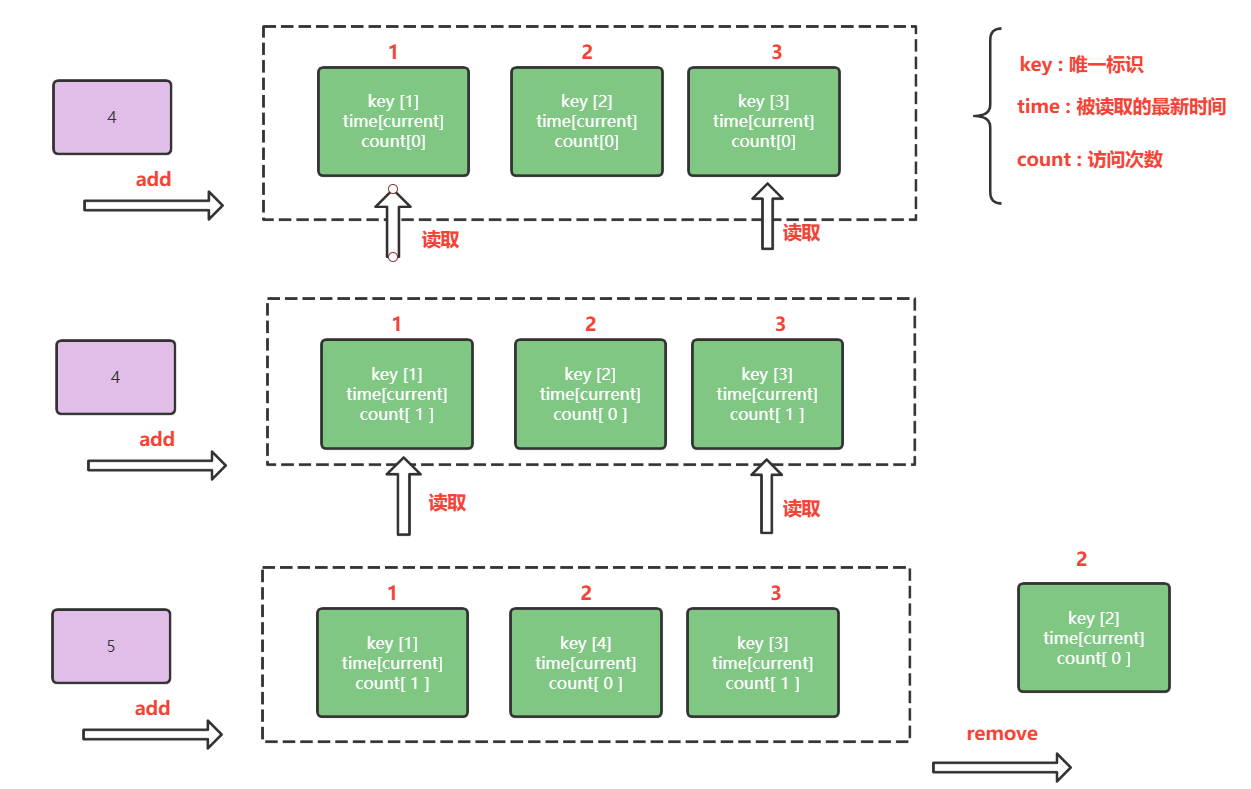
The working principle of LFU can be understood by referring to the figure above. The overall implementation idea is as follows:
- Define an object whose attributes include key (object unique identifier), addtime (object construction time), count (number of times the object is read);
- The object needs to be overloaded with a size comparison method, that is, to implement the Comparable interface. In the comparison method, first compare according to the number of reads of the object. If the number of reads is the same, then compare according to the latest read time
- Define a counter, which is used to identify the reading times of the object each time it is added or read, so as to facilitate fast search
According to the above idea, let's look at the following code directly
1. Define an entity object and implement the Comparable interface
/**
* object
*/
public class DataDto implements Comparable<DataDto> {
private String key;
private int count;
private long lastTime;
public DataDto(String key, int count, long lastTime) {
this.key = key;
this.count = count;
this.lastTime = lastTime;
}
@Override
public int compareTo(DataDto o) {
int compare = Integer.compare(this.count, o.count);
return compare == 0 ? Long.compare(this.lastTime, o.lastTime) : compare;
}
@Override
public String toString() {
return String.format("[key=%s,count=%s,lastTime=%s]", key, count, lastTime);
}
public String getKey() {
return key;
}
public void setKey(String key) {
this.key = key;
}
public int getCount() {
return count;
}
public void setCount(int count) {
this.count = count;
}
public long getLastTime() {
return lastTime;
}
public void setLastTime(long lastTime) {
this.lastTime = lastTime;
}
}
2. Main methods of operating LFU
/**
* Least recently used
* Time dimension + access times are jointly controlled
*/
public class SelfLFU {
private final int size = 3;
//The data storage capacity represents the maximum number of elements that can be stored in the container
private Map<String, Integer> counter = new HashMap<>();
//The key can quickly locate the object
private Map<String, DataDto> cache = new HashMap<>();
public void putData(String key, Integer value) {
Integer v = counter.get(key);
if (v == null) {
//If this element does not exist
if (counter.size() == size) {
//If the queue element has reached the maximum, you need to remove the element
removeElement();
}
//If the maximum queue limit is not reached, rebuild a new object
cache.put(key, new DataDto(key, 1, System.currentTimeMillis()));
} else {
//If it already exists in the counter cache, you only need to accumulate the access times of this element
addCount(key);
}
counter.put(key, value);
}
//The number of times to get the current element in the counter according to the key
public Integer get(String key) {
Integer value = counter.get(key);
if (value != null) {
addCount(key);
return value;
}
return null;
}
//Removing Elements
private void removeElement() {
DataDto dto = Collections.min(cache.values());
counter.remove(dto.getKey());
cache.remove(dto.getKey());
}
//The number of times the counter increments the key
private void addCount(String key) {
DataDto Dto = cache.get(key);
Dto.setCount(Dto.getCount() + 1);
Dto.setLastTime(System.currentTimeMillis());
}
//Printout results
private void print() {
System.out.println("counter=" + counter);
System.out.println("count=" + cache);
}
public static void main(String[] args) {
SelfLFU lfu = new SelfLFU();
//The first three capacities are not full, and 1, 2 and 3 are added
System.out.println("begin add 1‐3:");
lfu.putData("1", 1);
lfu.putData("2", 2);
lfu.putData("3", 3);
lfu.print();
//1,2 yes, 3 no, join 4, eliminate 3
System.out.println("begin read 1,2");
lfu.get("1");
lfu.get("2");
lfu.print();
System.out.println("begin add 4:");
lfu.putData("4", 4);
lfu.print();
//2 = 3 times, 1,4 = 2 times, but 4 is added late. When adding 5, 1 will be eliminated
System.out.println("begin read 2,4");
lfu.get("2");
lfu.get("4");
lfu.print();
System.out.println("begin add 5:");
lfu.putData("5", 5);
lfu.print();
}
}
Please focus on the putData method. Let's debug the key code through breakpoints to see how the data works
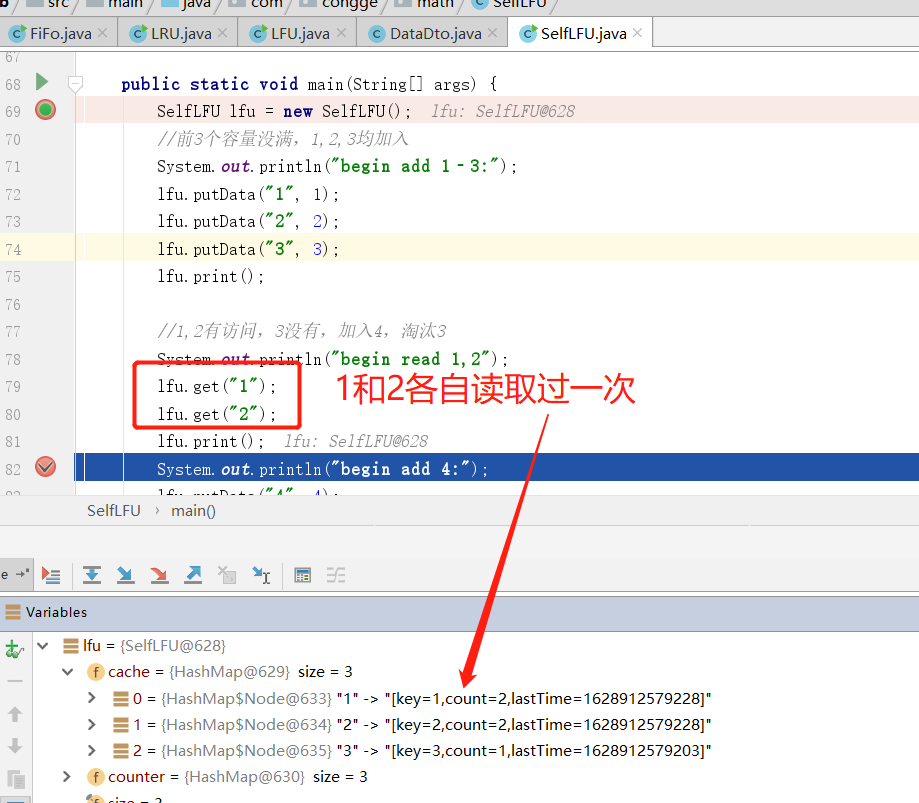
The figure shows three objects in memory after they are added to the object list. It can be found that 1 and 2 have been read once, so the value of count becomes 2, while the object represented by the key 3 has not been read, and the count is still 1
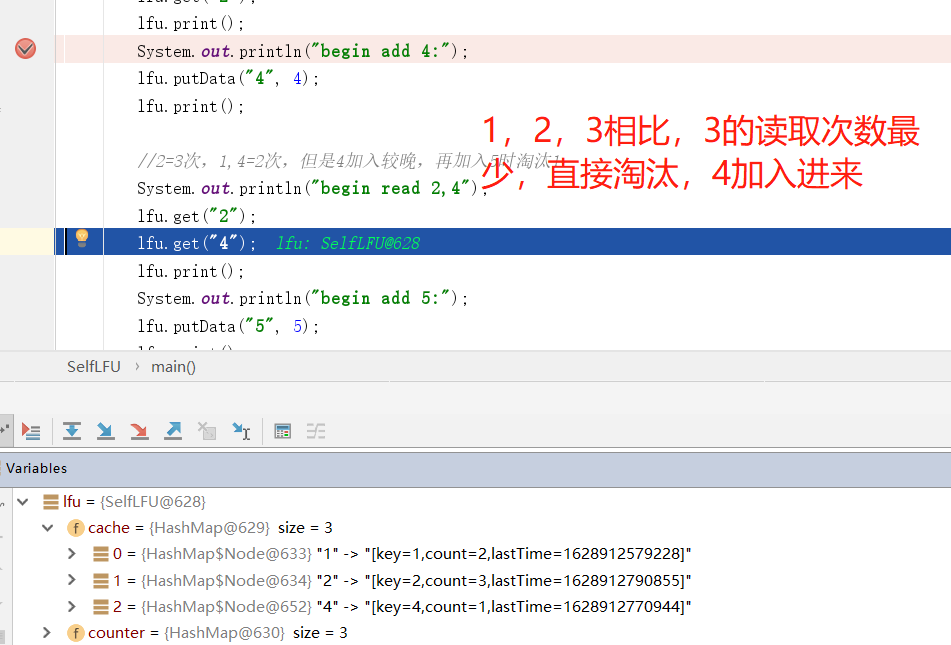
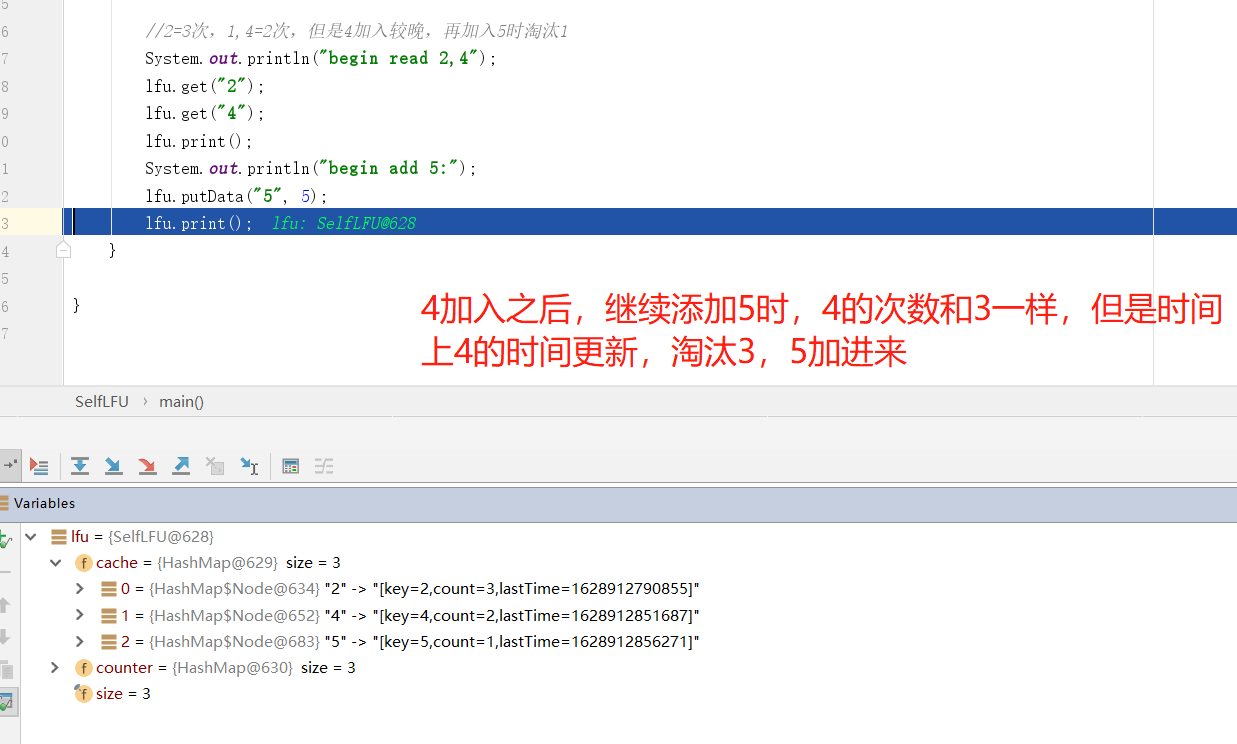

Through the above code breakpoint walkthrough, it can be found that the elimination strategy of LFU is implemented according to the expected estimation. In practical application, you can compare and understand it in combination with the relevant elimination strategies of redis official
This is the end of this article. Finally, thank you for watching!