preface
At present, the JDK version used is basically 1.8 or above. In most interviews, you will ask what is the difference between JDK7 and JDK8 versions of HashMap. HashMap is in jdk1 8, the red black tree is added on the basis of array + linked list. What are the benefits of doing so? In this paper, jdk1 8 version of HashMap to do a simple analysis.
1, Core attribute
Node node
The Node that stores data in HashMap uses Node. Take a look at the source code
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
...The assignment operation in the middle is gone
public final boolean equals(Object o) {
if (o == this)
return true;
if (o instanceof Map.Entry) {
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
if (Objects.equals(key, e.getKey()) &&
Objects.equals(value, e.getValue()))
return true;
}
return false;
}
}
From the Node node above, we can see that the linked list used by HashMap is one-way, and only the next Node has no previous Node; The equals() comparison of the content stored in HashMap is to compare the Key and Value. If the Key and Value are the same, the stored data is the same.
attribute
Similarly, let's first take a look at what the core attributes of HashMap mean. It's easy to understand when looking at the source code.
- DEFAULT_ INITIAL_ Capability: the default initialization capacity is 16. Here you can see that the source code does not directly write 16, but uses 1 < < 4. Why do you do this? This is because the author wants to tell us that its value is represented by 2n, which is used to reduce hash collision. The specific principle will be described later.
- MAXIMUM_ Capability: This represents the maximum capacity of HashMap. It is also represented by 2n. The maximum capacity is 230.
- DEFAULT_LOAD_FACTOR: loading factor. The default value is 0.75. Why use 0.75 instead of other values? What does this value mean? It's how much we currently use, such as 16 * 0.75 = 12. At this time, we need to expand the capacity. The problem of how to calculate is too deep. The official documents only tell us that this is the optimal value for time and space.
- TREEIFY_THRESHOLD: the threshold for converting red and black trees. The default value is 8, which means that red and black trees are used to store when the length of the linked list is greater than 8.
- UNTREEIFY_THRESHOLD: This is the opposite of the above. The threshold for converting to a linked list is 6 by default. It means that when the number of red and black trees is less than 6, they will be converted to a linked list.
- MIN_ TREEIFY_ Capability: the default value is 64, which is the same as that of the red black tree. It means that when the capacity of the array is greater than 64, it is converted to the red black tree.
- Table: table is a Node type array used to store the elements in the Map. Normally, when storing a Node element, it will find the corresponding subscript position in the table according to its key and put it in. When there are multiple data in the subscript position, these multiple data will form a linked list and be stored in the subscript position.
- entrySet: Needless to say, there is a slice of Set type when traversing the Map Set.
- size: like other sets, it is used to record the number of key value pairs in the Map.
- modCount: the ConcurrentModificationException exception will be used to record the operation of the collection. If it changes, it will be CME.
- threshold: This is the actual value of capacity expansion. 0.75 above is the loading factor. This is 16 * 0.75 = 12. This is a specific value.
- loadFactor: load factor, which is 0.75 by default.
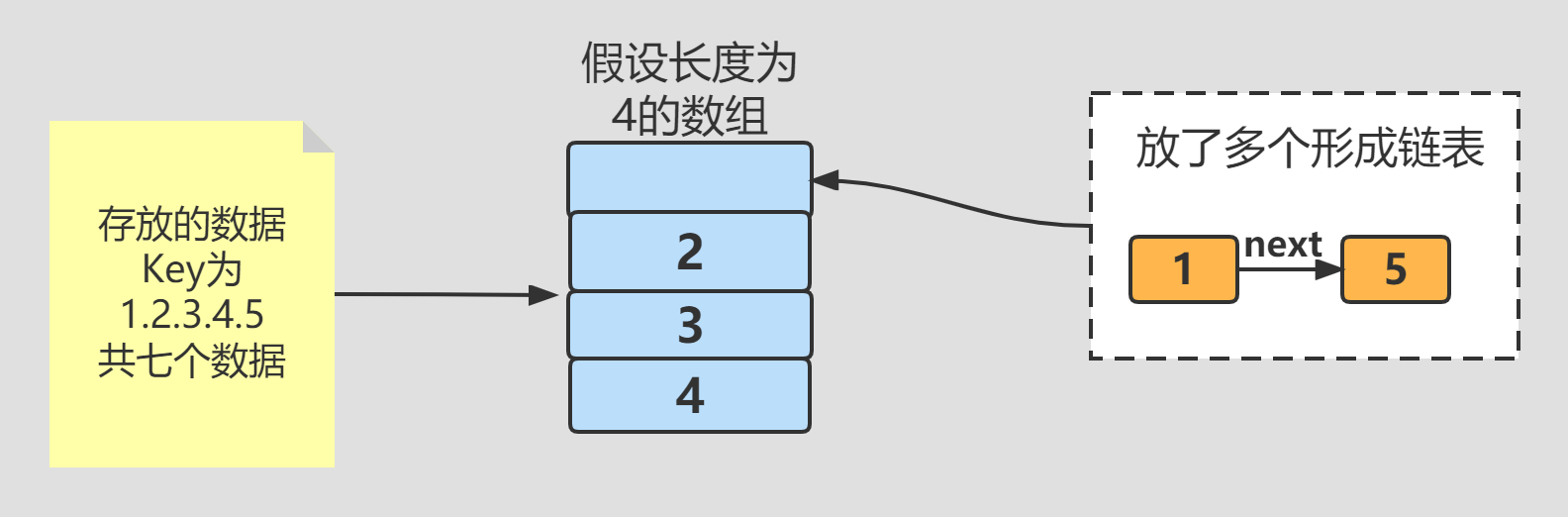
At first, HashMap stores data in this way. An array table is used to store data. Suppose five data with key s of 12345 are put in turn. When the last 5 is stored, the subscript finds the first position of the array. Since 1 has been stored here, 1 - > 5 forms a linked list structure. As mentioned above, when the length of the table array is greater than 64 and the length of the linked list is greater than 8, it will be stored in a red black tree.
2, Core method
1. Construction method
Nonparametric structure
public HashMap() {
//Nonparametric construction is to assign a value to the loading factor
this.loadFactor = DEFAULT_LOAD_FACTOR;
}
Parametric construction passing initial size and loading factor
public HashMap(int initialCapacity, float loadFactor) {
...This is a bunch of checking whether the parameters passed are legal
this.loadFactor = loadFactor; //Load factor assignment operation
//Calculate the initial value of the threshold value. Here, it is not how much is transmitted, but find the data with the power of the smallest 2 larger than this number. You can have a unit test by yourself
this.threshold = tableSizeFor(initialCapacity);
}
Pass the collection of Map type to regenerate the parametric construction of the collection
public HashMap(Map<? extends K, ? extends V> m) {
this.loadFactor = DEFAULT_LOAD_FACTOR; //Assignment initialization size threshold
putMapEntries(m, false);
}
final void putMapEntries(Map<? extends K, ? extends V> m, boolean evict) {
int s = m.size(); //Gets the size of the transfer Map
if (s > 0) {
if (table == null) { //If the array has not been created at this time, initialize the creation of the array
float ft = ((float)s / loadFactor) + 1.0F;
int t = ((ft < (float)MAXIMUM_CAPACITY) ?
(int)ft : MAXIMUM_CAPACITY);
if (t > threshold)
threshold = tableSizeFor(t);
}
else if (s > threshold) //If the array is created, check whether the size of the array is enough to resize and expand
resize();
for (Map.Entry<? extends K, ? extends V> e : m.entrySet()) { //Slice assignment
K key = e.getKey();
V value = e.getValue();
putVal(hash(key), key, value, false, evict); //The specific methods will be explained later
}
}
}
resize() resize
The above-mentioned construction method uses the resize () capacity expansion method. Let's take a look at the implementation directly here, including the increase of put() later, which also involves resize().
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
//Record the length of the original array
int oldCap = (oldTab == null) ? 0 : oldTab.length;
//Record the original threshold
int oldThr = threshold;
//New array length and threshold
int newCap, newThr = 0;
if (oldCap > 0) { //If the original array length is greater than 0
if (oldCap >= MAXIMUM_CAPACITY) { //The length of the original array is greater than the maximum value of 2 ^ 30, which is set to the maximum value of int 2 ^ 32
threshold = Integer.MAX_VALUE;
return oldTab;
}
//The length of the new array is old*2. If it is less than the maximum length and the original capacity is greater than the default length
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; //The new threshold is the old threshold * 2
}
else if (oldThr > 0) // If the old threshold > 0, the new array length is the old threshold size
newCap = oldThr;
else { //The initial value is loaded for the first time
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) { //The new threshold is 0, and the above operation does not involve threshold modification
float ft = (float)newCap * loadFactor; //The new threshold is the array capacity * 0.75, and the following is the judgment maximum value
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
//The new threshold and array length are obtained, and the assignment operation is carried out
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
...Recalculation after capacity expansion is omitted index The problem is relatively simple, which is based on the previous data hash The subscript position of the value, after capacity expansion hash The corresponding position is wrong. You need to play all the data again
return newTab;
}
put() put data value
The stored value of HashMap is the putVal() method of transfer
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; //Used to store the contents of the array
Node<K,V> p; //Node representing subscript position
int n, i; //n is the length of the array and i is the index subscript value of the array
if ((tab = table) == null || (n = tab.length) == 0) //The current array is empty. Start to initialize expansion
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null) //This is the node to obtain the subscript position. If there is no new node, it will be stored directly
tab[i] = newNode(hash, key, value, null);
else { //If the subscript position already has data
Node<K,V> e; K k; //e is used to temporarily store data and k is used to temporarily store key values
if (p.hash == hash && //If the Hash value and the Key are equal, assign the value directly
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode) //If the data obtained is red black tree
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else { //If the hash value is not equal to the key
for (int binCount = 0; ; ++binCount) { //This is an endless loop. Jump out of the loop through the inner operation
//Assuming that p.next is not empty, e=p.next is traversed until it is empty
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null); //Hang the value directly behind the linked list
if (binCount >= TREEIFY_THRESHOLD - 1) //When the length of the linked list reaches the threshold, that is, 8 is converted into a tree structure
treeifyBin(tab, hash);
break; //Jump out of loop
}
//If the Key and hash values are equal during traversal, the loop will jump out
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e; //e=p.next is used to cycle down the linked list
}
}
if (e != null) { //Finally, if there is a node at the subscript position, replace it with a numerical value
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e); //It's useless for Hash. Leave it to the method implemented by the subclass of LinkedHashMap
return oldValue;
}
}
++modCount; //CME logo
if (++size > threshold)
resize(); //Capacity expansion
afterNodeInsertion(evict); //It's useless for Hash. Leave it to the method implemented by the subclass LinkedHashMap
return null;
}
In fact, ignoring the red black tree and capacity expansion, the put() method is relatively simple, which can be roughly divided into these steps:
- Check whether there is data stored in the subscript position in the array. If there is no new data directly created in the subscript position.
- There is data at the subscript position of the array. Traverse the linked list of subscript positions. If you can't find an equal key after traversal, hang it directly at the end
- If an equal key is found during traversal, record the node
- Replace the value of node that finds the same key.
Let's take another look at the red black tree operation involved in put. First, when the p node we took is a tree node, hang the value on the tree
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
//Here are the specific methods
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
int h, K k, V v) {
Class<?> kc = null;
boolean searched = false; //Search flag for tree
//Get the root node. If the parent node of node p operated above is empty, then node p is the root node
TreeNode<K,V> root = (parent != null) ? root() : this;
//Loop through nodes from the root node
for (TreeNode<K,V> p = root;;) {
//dir is the direction of traversal, ph is the hash value of p, and pk is the key value of p
int dir, ph; K pk;
if ((ph = p.hash) > h) //If the hash value of the current node is greater than the given hash value, put it to the left
dir = -1; //-1 stands for left
else if (ph < h)
dir = 1; //1 stands for right
else if ((pk = p.key) == k || (k != null && k.equals(pk))) //If the key of the current node is the same as the given key
return p; //Directly return the current node p
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0) {
if (!searched) {
TreeNode<K,V> q, ch;
searched = true; //Traversal completion modify traversal ID
if (((ch = p.left) != null && //Always traverse find to find nodes with the same key
(q = ch.find(h, k, kc)) != null) ||
((ch = p.right) != null &&
(q = ch.find(h, k, kc)) != null))
return q; //Return the node found after finding
}
//At this time, the node corresponding to the key is not found. Compare the size of the two keys to determine the direction
dir = tieBreakOrder(k, pk);
}
TreeNode<K,V> xp = p;
//The direction has been judged again and new nodes have been hung in this direction
if ((p = (dir <= 0) ? p.left : p.right) == null) {
Node<K,V> xpn = xp.next; //The next node of the current node
TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn); //Create a new node
if (dir <= 0) //Hang on the left
xp.left = x;
else
xp.right = x; //Hang on the right
xp.next = x; //Hang on the next node of the linked list
x.parent = x.prev = xp; //The parent node of the new node and its previous node are attached to the current node
if (xpn != null)
((TreeNode<K,V>)xpn).prev = x;
//This is a red black tree re rotation balancing operation
moveRootToFront(tab, balanceInsertion(root, x));
return null;
}
}
}
In fact, the code logic is also very simple. Looking at the complexity, there are too many judgment conditions:
- Get the root node and start traversing the tree.
- In the process of traversing the tree, find the tree node with the same key. If it is found, it will be returned directly.
- If not found, determine the direction between the current node and the given node.
- After determining the direction, hang a new node in the corresponding direction.
- The red black tree performs self balancing operation.
Another method is to convert the linked list into a red black tree if the length of the linked list reaches the threshold of converting into a tree:
treeifyBin(tab, hash);
//Take a look at the specific conversion process
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
//The first is capacity expansion judgment
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
resize();
//
else if ((e = tab[index = (n - 1) & hash]) != null) {
//These two represent head node and tail node respectively
TreeNode<K,V> hd = null, tl = null;
do {
//Start the loop to change the node into a tree node
TreeNode<K,V> p = replacementTreeNode(e, null);
if (tl == null) //In the first execution, the tail node is empty, and the newly converted node is set as the head node
hd = p;
else {
p.prev = tl; //The previous node of the current node points to the tail node
tl.next = p; //The next node of the tail node points to the current node
}
tl = p; //The tail node is replaced by the current node, which means that each new traversal is put from the tail
} while ((e = e.next) != null);
//The converted two-way linked list replaces the linked list of the original array position
if ((tab[index] = hd) != null)
hd.treeify(tab); //Start to build the two-way linked list into a tree structure
}
}
After looking at the above code, the previous part mainly constructs the original one-way linked list into a two-way linked list of tree nodes. Finally, the two-way linked list is constructed into a tree structure by treeify().
final void treeify(Node<K,V>[] tab) {
TreeNode<K,V> root = null; //root node
//Here, use the method of the point of the head node, the head node of the bidirectional linked list represented by this, and start traversing the bidirectional linked list
for (TreeNode<K,V> x = this, next; x != null; x = next) {
next = (TreeNode<K,V>)x.next; //Take out the next node
x.left = x.right = null; //Clear the left and right child nodes of the current node first
//Set the current node to root for the first time, but not directly
if (root == null) {
x.parent = null;
x.red = false;
root = x;
}else { //The second traversal starts to hang the tree node
K k = x.key; //Get the key and hash values of the current node
int h = x.hash;
Class<?> kc = null;
//The current node starts the cycle
for (TreeNode<K,V> p = root;;) {
//Similarly, dir indicates the direction. The following two are pHash and pKey
int dir, ph;
K pk = p.key;
//Judge whether it belongs to the left child node or the right child node according to the hash value
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
//The hash values are equal, and then compare the key and class to determine the direction
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0)
dir = tieBreakOrder(k, pk);
//Start hanging nodes under the current node
TreeNode<K,V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
x.parent = xp; //Hang parent node
if (dir <= 0) //According to the direction, the child nodes are hung on the left and right
xp.left = x;
else
xp.right = x;
root = balanceInsertion(root, x); //After each new addition, self balancing is done, that is, the five insertion methods of red and black trees
break;
}
}
}
}
moveRootToFront(tab, root); //Self equilibrium of red black tree
}
The general idea is to cycle from the first node of the linked list, set the first node as root, determine the direction by comparing hash, key, class and other information, and then insert the hanging node from below. At this time, we specify the root at will. After hanging, we can find the real root and change the red black tree to the standard state.
The above simple analysis of HashMap mainly focuses on the whole logic of put method. You don't need to know how to do each step, but only need to know the general logic. Looking at the above code analysis, we should understand the importance of code logic. When we write a complex code, we'd better first write the steps of what to do in the first step and what to do in the second step, and then fill in the code, so that the code will not be messy. If it's too complex, we'd better write a method at each step to ensure the readability of the code.
The get() method behind HashMap will not be analyzed, because the get() operation is already involved in put().
Differences between HashMap in JDK7 and JDK8
- First of all, it must be the underlying structure. The array + linked list used in JDK7. When there are too many hash conflicts, the linked list stored in the corresponding location is too long, which affects the later query efficiency. Therefore, the red black tree is introduced in JDK8. When the linked list reaches a certain number, the red black tree is used. Of course, the red black tree also has disadvantages, that is, the operation is too complex when adding, including self balancing, The efficiency of new addition in red black tree is low. It's OK to talk about it in the interview.
- In fact, there is a vulnerability in HashMap in JDK7, that is, the linked list is inserted at the head, which will cause an endless loop under certain conditions (especially multi-threaded capacity expansion). In JDK8, it is modified to tail insertion.