As soon as the array comes in, it will encounter the first threshold quickport_ Threshold (286). According to the annotation, not all those below this threshold enter Quicksort. Click sort(a, left, right, true); method:

     // Use Quicksort on small arrays
        if (right - left < QUICKSORT_THRESHOLD) {
            sort(a, left, right, true);
            return;
        }

After clicking in, we see the second threshold INSERTION_SORT_THRESHOLD (47). If the element is less than the threshold value of 47, it is sorted by insertion. Looking down, it is true:

      if (length < INSERTION_SORT_THRESHOLD) {
            if (leftmost) {
                /*
                 * Traditional (without sentinel) insertion sort,
                 * optimized for server VM, is used in case of
                 * the leftmost part.
                 */
                for (int i = left, j = i; i < right; j = ++i) {
                    int ai = a[i + 1];
                    while (ai < a[j]) {
                        a[j + 1] = a[j];
                        if (j-- == left) {
                            break;
                        }
                    }
                    a[j + 1] = ai;
                }
            }

Elements less than 47 are sorted by insertion

As for greater than INSERTION_SORT_THRESHOLD (47) uses a quick sort method:
1. Pick out five elements from the sequence, called "pivot";
2. Reorder the sequence. All elements smaller than the benchmark value are placed in front of the benchmark, and all elements larger than the benchmark value are placed behind the benchmark (the same number can be on either side). After the partition exits, the benchmark is in the middle of the sequence. This is called a partition operation;
3. Recursively sort the subsequence less than the reference value element and the subsequence greater than the reference value element.

Quick Sort

This is less than the threshold quickport_ There are two cases of threshold (286). For those greater than 286, it will enter Merge Sort, but before that, it has a small action:

    // Check if the array is nearly sorted
        for (int k = left; k < right; run[count] = k) {
            if (a[k] < a[k + 1]) { // ascending
                while (++k <= right && a[k - 1] <= a[k]);
            } else if (a[k] > a[k + 1]) { // descending
                while (++k <= right && a[k - 1] >= a[k]);
                for (int lo = run[count] - 1, hi = k; ++lo < --hi; ) {
                    int t = a[lo]; a[lo] = a[hi]; a[hi] = t;
                }
            } else { // equal
                for (int m = MAX_RUN_LENGTH; ++k <= right && a[k - 1] == a[k]; ) {
                    if (--m == 0) {
                        sort(a, left, right, true);
                        return;
                    }
                }
            }

            /*
             * The array is not highly structured,
             * use Quicksort instead of merge sort.
             */
            if (++count == MAX_RUN_COUNT) {
                sort(a, left, right, true);
                return;
            }
        }

The main function here is to see whether the array has a structure: the actual logic is grouping and sorting, and each descending order is a group, such as 1,9,8,7,6,8. 9 to 6 are in descending order, which is a group, and then the descending group is arranged in ascending order: 1,6,7,8,9,8. Then continue to look behind the last 8...

Whenever such a descending group is encountered, + count, when count is greater than MAX_RUN_COUNT (67), which is judged that the array does not have a structure (that is, the data rises and falls from time to time), and then sent to the previous sort method (The array is not highly structured,use Quicksort instead of merge sort).

If count is less than MAX_RUN_COUNT (67) indicates that this array has some structure. Go on to merge and sort as follows:

   // Determine alternation base for merge
        byte odd = 0;
        for (int n = 1; (n <<= 1) < count; odd ^= 1);

From here, we officially enter Merge Sort!

  // Merging
        for (int last; count > 1; count = last) {
            for (int k = (last = 0) + 2; k <= count; k += 2) {
                int hi = run[k], mi = run[k - 1];
                for (int i = run[k - 2], p = i, q = mi; i < hi; ++i) {
                    if (q >= hi || p < mi && a[p + ao] <= a[q + ao]) {
                        b[i + bo] = a[p++ + ao];
                    } else {
                        b[i + bo] = a[q++ + ao];
                    }
                }
                run[++last] = hi;
            }
            if ((count & 1) != 0) {
                for (int i = right, lo = run[count - 1]; --i >= lo;
                    b[i + bo] = a[i + ao]
                );
                run[++last] = right;
            }
            int[] t = a; a = b; b = t;
            int o = ao; ao = bo; bo = o;
        }
    

Merge Sort

Summary:

Summary:
From the above analysis, arrays Sort is not a single sort, but a combination of insert sort, quick sort and merge sort. Therefore, I draw a flow chart:

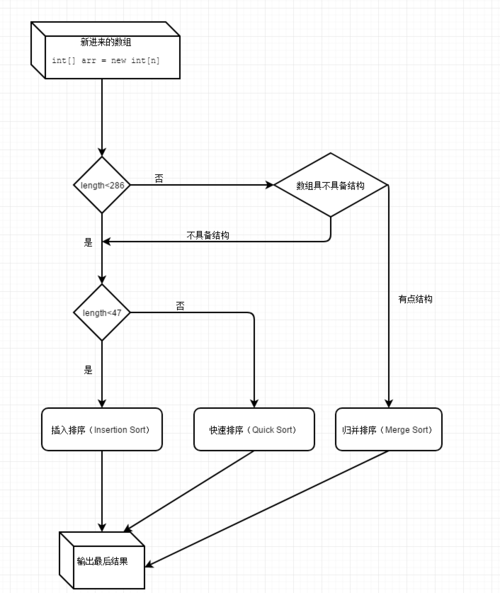
Original drawing, please indicate the source for forwarding

Reproduced in Analyzing arrays. In JDK8 The underlying principle of sort and the selection of sorting algorithm