Ant colony algorithm for TSP problem

Introduction to TSP issues

Traveling businessmen need to visit n cities and finally return to the starting city. They are required to visit each city only once. The optimization goal is to minimize the sum of distances.

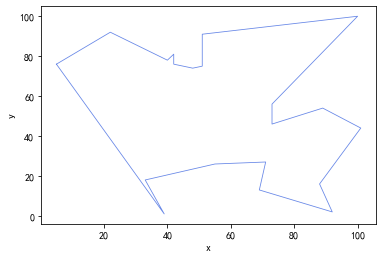
Example solution results

20 city coordinates: (88, 16), (42, 76), (5, 76), (69, 13), (73, 56), (100, 100), (22, 92), (48, 74), (73, 46), (39, 1), (51, 75), (92, 2), (101, 44), (55, 26), (71, 27), (42, 81), (51, 91), (89, 54), (33, 18), (40, 78)
The result path is as follows:

Introduction to ant colony algorithm

Basic principle of ant colony algorithm

1. In the process of walking, ants will choose the road based on pheromone, choose the road with strong pheromone, and release pheromone in the path of walking. For the road that all ants have not passed, they will choose a road at random;
2. The pheromone concentration released by ants is related to the length, usually inversely proportional to the path length;
3. The path with high pheromone concentration will be selected by ants with greater probability to form positive feedback, and the pheromone concentration on the shortest path will become larger and larger. Finally, the ant colony will follow this shortest path.

Pheromone calculation formula, transfer probability, pheromone importance factor, heuristic function importance factor, pheromone volatilization factor and other details can be referred to Detailed explanation of ant colony algorithm and The solution of TSP -- ant colony algorithm

Two key steps of the algorithm

1. Selection: select the next city for the ant. The path with more pheromones has a high probability of being selected, which can be realized by roulette algorithm;
2. Pheromone update: recalculate the pheromone after a period of time (after the ant has completed a city or a complete path) (calculation method: historical accumulated pheromone - pheromone volatilization + ant walking release), There are three common methods for ant walking release: ant cycle algorithm (Q/L is used to calculate the ant walking release part after the ant walks a complete path, Q represents the amount of pheromone released by the ant, which is a constant, l represents the total length of the path), ant density algorithm (Q represents the ant walking release after the ant walks a city) Ant quantity algorithm (ant quantity, after an ant walks through a city, the ant's walking release is represented by Q/dij, and dij represents the distance between cities i and j).

Ant colony algorithm design

In the design of this algorithm, there are two layers of loops. The outer loop is the cycle of iteration times, and the inner loop traverses each ant. The pheromone increment updates the current pheromone after each ant walks the complete path, while the pheromone volatilization updates the current pheromone only after each generation of ants walk. The process is as follows:

# -*- coding: utf-8 -*-
"""
Tabu search algorithm TSP problem
 Random in (0),100)20 points generated from 2D plane
 Distance minimization
"""
import math
import random
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']  # Add this bar to make the graphics display Chinese


#Calculate the path distance, that is, the evaluation function
def calFitness(line,dis_matrix):
    dis_sum = 0
    dis = 0
    for i in range(len(line)-1):
        dis = dis_matrix.loc[line[i],line[i+1]]#Calculate distance
        dis_sum = dis_sum+dis
    dis = dis_matrix.loc[line[-1],line[0]]
    dis_sum = dis_sum+dis
    
    return round(dis_sum,1)


def intialize(CityCoordinates,antNum):
    """
    Initialization, assigning the initial city to the ant
    Input: CityCoordinates-City coordinates;antNum-Ant number 
    Output: cityList-List of initial cities of ants, and record the initial cities of ants;cityTabu-Ant city taboo list, which records that ants have not passed through the city
    """
    cityList,cityTabu = [None]*antNum,[None]*antNum#initialization
    for i in range(len(cityList)):
        city = random.randint(0, len(CityCoordinates)-1)#Initial City, the default City serial number is 0, and the calculation starts
        cityList[i] = [city]
        cityTabu[i] = list(range(len(CityCoordinates)))
        cityTabu[i].remove(city)
    
    return cityList,cityTabu


def select(antCityList,antCityTabu,trans_p):
    '''
    Roulette selection: select all cities according to the departure city
    Input: trans_p-Probability matrix;antCityTabu-Urban taboo list, i.e. without passing through the city;
    Output: full city path-antCityList;
    '''
    while len(antCityTabu) > 0:  
        if len(antCityTabu) == 1:
            nextCity = antCityTabu[0]
        else:
            fitness = []
            for i in antCityTabu:fitness.append(trans_p.loc[antCityList[-1],i])#Take out the city transfer probability corresponding to antCityTabu
            sumFitness = sum(fitness)
            randNum = random.uniform(0, sumFitness)
            accumulator = 0.0
            for i, ele in enumerate(fitness):
                accumulator += ele
                if accumulator >= randNum:
                    nextCity = antCityTabu[i]
                    break
        antCityList.append(nextCity)
        antCityTabu.remove(nextCity)
    
    return antCityList


def calTrans_p(pheromone,alpha,beta,dis_matrix,Q):
    '''
    Calculate the transition probability according to the pheromone
    Input: pheromone-Current pheromone; alpha-Pheromone importance factor; beta-Heuristic function importance factor; dis_matrix-Distance matrix between cities; Q-Pheromone constant;
    Output: current pheromone+increment-transProb
    '''
    transProb = Q/dis_matrix # Initialize the transProb storage transfer probability and calculate the increment at the same time
    for i in range(len(transProb)):
        for j in range(len(transProb)):
            transProb.iloc[i,j] = pow(pheromone.iloc[i,j], alpha) * pow(transProb.iloc[i,j], beta)
    
    return transProb


def updatePheromone(pheromone,fit,antCity,rho,Q):
    '''
    Update pheromone, ant week algorithm
    Input: pheromone-Current pheromone; fit-Path length; antCity-route; rho-ρPheromone volatilization factor; Q-Pheromone constant
    Output: updated pheromone-pheromone
    '''
    for i in range(len(antCity)-1):
        pheromone.iloc[antCity[i],antCity[i+1]] += Q/fit
    pheromone.iloc[antCity[-1],antCity[0]] += Q/fit
    
    return pheromone

#Draw a path map
def draw_path(line,CityCoordinates):
    x,y= [],[]
    for i in line:
        Coordinate = CityCoordinates[i]
        x.append(Coordinate[0])
        y.append(Coordinate[1])
    x.append(x[0])
    y.append(y[0])
    
    plt.plot(x, y,'r-', color='#4169E1', alpha=0.8, linewidth=0.8)
    plt.xlabel('x')
    plt.ylabel('y')
    plt.show()


if __name__ == '__main__':
    #parameter
    CityNum = 20#Number of cities
    MinCoordinate = 0#Minimum value of two-dimensional coordinates
    MaxCoordinate = 101#Maximum value of two-dimensional coordinates
    iterMax = 100#Number of iterations
    iterI = 1#Current iterations
    #ACO parameters
    antNum = 50#Ant number 
    alpha = 2#Pheromone importance factor
    beta = 1#Heuristic function importance factor
    rho = 0.2#Pheromone volatilization factor
    Q = 100.0#constant
    
    best_fit = math.pow(10,10)#Large initial value and store the optimal solution
    best_line = []#Storage optimal path
    
    #Randomly generate city data. The city serial number is 0,1,2,3
    # CityCoordinates = [(random.randint(MinCoordinate,MaxCoordinate),random.randint(MinCoordinate,MaxCoordinate)) for i in range(CityNum)]
    CityCoordinates = [(88, 16),(42, 76),(5, 76),(69, 13),(73, 56),(100, 100),(22, 92),(48, 74),(73, 46),(39, 1),(51, 75),(92, 2),(101, 44),(55, 26),(71, 27),(42, 81),(51, 91),(89, 54),(33, 18),(40, 78)]
    
    #Calculate the distance between cities and generate a matrix
    dis_matrix = pd.DataFrame(data=None,columns=range(len(CityCoordinates)),index=range(len(CityCoordinates)))
    for i in range(len(CityCoordinates)):
        xi,yi = CityCoordinates[i][0],CityCoordinates[i][1]
        for j in range(len(CityCoordinates)):
            xj,yj = CityCoordinates[j][0],CityCoordinates[j][1]
            if (xi==xj) & (yi==yj):
                dis_matrix.iloc[i,j] = round(math.pow(10,10))
            else:
                dis_matrix.iloc[i,j] = round(math.sqrt((xi-xj)**2+(yi-yj)**2),2)
    
    pheromone = pd.DataFrame(data=Q,columns=range(len(CityCoordinates)),index=range(len(CityCoordinates)))#Initialize pheromone. All paths are Q
    trans_p = calTrans_p(pheromone,alpha,beta,dis_matrix,Q)#Calculate the initial transition probability
    
    while iterI <= iterMax:
        '''
        The pheromone reduction caused by environmental factors is updated once in each generation. After each ant in each generation completes the path, the pheromone increment update (using ant week model) and transfer probability update are carried out;
        At the beginning of each generation, the starting city of ants is initialized first;
        '''
        antCityList,antCityTabu = intialize(CityCoordinates,antNum)#Initialize City
        fitList = [None]*antNum#Fitness list
        
        for i in range(antNum):#Select the cities of follow-up routes according to the transfer probability, and calculate the adaptation value
            antCityList[i] = select(antCityList[i],antCityTabu[i],trans_p)
            fitList[i] = calFitness(antCityList[i],dis_matrix)#Fitness, i.e. path length
            pheromone = updatePheromone(pheromone,fitList[i],antCityList[i],rho,Q)#Update current ant pheromone increment
            trans_p = calTrans_p(pheromone,alpha,beta,dis_matrix,Q)
        
        if best_fit >= min(fitList):
            best_fit = min(fitList)
            best_line = antCityList[fitList.index(min(fitList))]
            
        print(iterI,best_fit)#Print current algebra and best fit values
        iterI += 1#Iteration count plus one
        pheromone = pheromone*(1-rho)#Pheromone volatilization update
    
    print(best_line)#Path order
    draw_path(best_line,CityCoordinates)#Draw a path map