Why Choose Jump Table
At present, the commonly used balanced data structures are: B tree, red-black tree, AVL tree, Splay Tree, Treep and so on. Imagine giving you a sketch paper, a pen, an editor. Can you instantly implement a red-black tree, or an AVL tree? It's hard. It takes time. It takes a lot of details. It's a lot of trouble to refer to a bunch of trees like algorithms and data structures, as well as the code on the Internet. Jump table is a randomized data structure. At present, open source software Redis and LevelDB are used for it. Its efficiency is similar to that of red-black tree and AVL tree, but the principle of jump table is quite simple. As long as you can operate the linked list skillfully, you can easily implement a SkipList.

Search for ordered tables
Consider an ordered table

The number of searching elements < 23, 43, 59 > from the ordered table is < 2, 4, 6 > and the total number of comparisons is 2 + 4 + 6 = 12. Are there any optimized algorithms? Link lists are ordered, but binary lookups cannot be used. Similar to binary search tree, we extract some nodes as index. The following structure is obtained:

Here we extract < 14, 34, 50, 72 > as a first-level index, so that we can reduce the number of comparisons when searching. We can also extract some elements from the first-level index and use them as the second-level index to form the following structure:

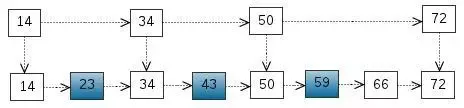
There are not many elements here, which can not reflect the advantages. If there are enough elements, this index structure can reflect the advantages.

Jump table
The following structure is the jump table:
Among them - 1 denotes INT_MIN, the minimum value of the list, 1 denotes INT_MAX, and the maximum value of the list.

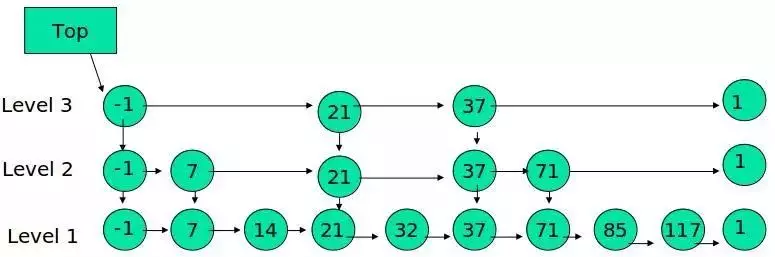
The jump table has the following properties:
(1) It consists of many layers.
(2) Each layer is an ordered list.
(3) The list at the bottom (Level 1) contains all elements.
(4) If an element appears in Level i's list, it will also appear in the list below Level I.
(5) Each node contains two pointers, one pointing to the next element in the same list and one pointing to the next layer.

Jump table search
Example: Find element 117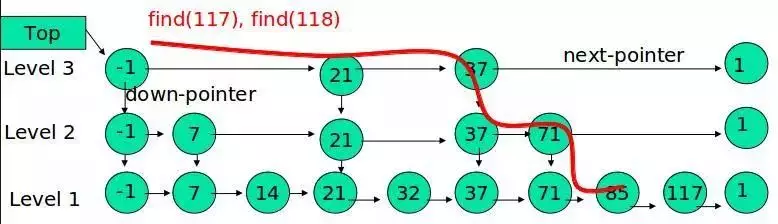

(1) Compare 21, bigger than 21. Look back.
(2) Compare 37, bigger than 37, smaller than the maximum value of the list. Start from the lower layer of 37.
(3) Compare 71, bigger than 71, smaller than the maximum value of the list. Start from the lower layer of 71.
(4) Compare 85, bigger than 85. Look for it from the back.
(5) Compare 117, equal to 117, find the node.

Insertion of Jump Table
Firstly, determine the number of layers K to be occupied by the element (in the form of coin dropping, this is completely random)
Then insert elements into the list of Level 1... Level K layers.
Example: Insert 119, K = 2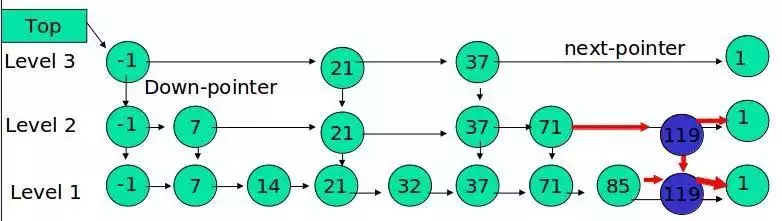

If K is greater than the number of layers in the list, a new layer is added.
Example: insert 119, K = 4

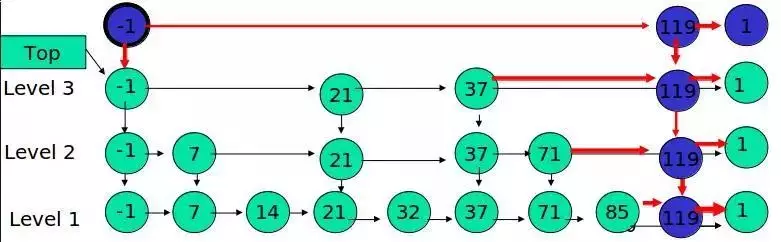
Height of Jump Meter
The jump table of n elements, when inserting each element, must do an experiment to determine the number of layers K occupied by the element. The height of the jump table is equal to the maximum K produced in the n experiments, to be continued...

Spatial Complexity Analysis of Jump Table
According to the above analysis, the expected height of each element is 2, and the expected number of nodes of a jump table with size n is 2n.

Deletion of jump tables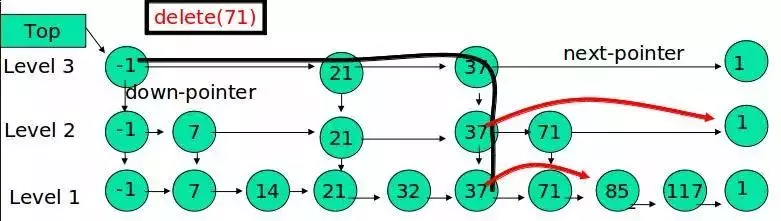

Find the node containing x in each layer and delete the node using the standard delete from list method.

Example: Delete 71

Okay, let's finish with the jump table above. Next, let's look at how to implement the jump table in Redis. We know that the bottom layer of zset ordered set in Redis uses jump tables to store data, so let's look at the zset structure. As a rule, I think redis source code starts with commands, so let's see what zadd does.

Before we talk about the jump table implemented by Redis, let's talk about the composition of the ordered set of Redis.

/**

• ZSETs use a specialized version of Skiplists
• Data Nodes in Jump Table
  */

typedef struct zskiplistNode {

sds ele;
double score;
// Back pointer
struct zskiplistNode *backward;
// layer
struct zskiplistLevel {
    // Forward pointer
    struct zskiplistNode *forward;
    /**
     * Spans are actually used to rank elements.
     * In the process of finding a node, the span of all the layers visited along the way is accumulated.
     * The result is the position of the target node in the jump table.
     */
    unsigned long span;
} level[];

} zskiplistNode;

/**

• Jump table structure
  */

typedef struct zskiplist {

struct zskiplistNode *header, *tail;
unsigned long length;
int level;

} zskiplist;

/**

• Ordered aggregate structure
  */

typedef struct zset {

/*
 * Redis It will make up all the elements and values in the jump table.
 * key-value The form is kept in the dictionary.
 * todo: Note: This dictionary is not a dictionary in Redis DB, but an ordered set.
 */
dict *dict;
/*
 * The pointer of the jump table pointed at the bottom
 */
zskiplist *zsl;

} zset;
zadd command (add elements)
The reason for starting from zadd is that when we first use zadd to add ordered sets, the ordered sets do not exist. redis needs to create an ordered set first, so that we can start from the source, so let's look at the implementation of zaddCommand method.

/**

• Adding elements to ordered collections
  *
• @ param c client data
  */

void zaddCommand(client *c) {

zaddGenericCommand(c, ZADD_NONE);

}
As you can see from the above, the underlying method is the zaddGenericCommand() method, so let's move on.

void zaddGenericCommand(client *c, int flags) {

// Ignore some interference code first
...
/* Find out from the dictionary whether the ordered collection exists or not, and create it if it does not. */
zobj = lookupKeyWrite(c->db, key);
if (zobj == NULL) {
    if (xx) goto reply_to_client; /* No key + XX option: nothing to do. */
    // If the ziplist structured storage is turned off in the configuration file, an ordered collection stored with jump tables is created directly
    if (server.zset_max_ziplist_entries == 0 ||
        server.zset_max_ziplist_value < sdslen(c->argv[scoreidx + 1]->ptr)) {
        zobj = createZsetObject();
    } else {
        // From this we can see that the underlying ordered collection uses ziplist to store elements in the first place, and ziplist will come back next time.
        zobj = createZsetZiplistObject();
    }
    // Save our newly created ordered collection in the dictionary
    dbAdd(c->db, key, zobj);
} else {
    // Structural error reporting that is not an ordered set
    ...
}

for (j = 0; j < elements; j++) {
    double newscore;
    score = scores[j];
    int retflags = flags;

    ele = c->argv[scoreidx + 1 + j * 2]->ptr;
    // Here we finally see the code for adding elements to zset.
    int retval = zsetAdd(zobj, score, ele, &retflags, &newscore);
    ...
}
...

}
Call chain is very long, or we need to be patient and continue to look down!

int zsetAdd(robj zobj, double score, sds ele, int flags, double *newscore) {

 // Ignore interference code
 ...
/* The encoding format is ziplist */
if (zobj->encoding == OBJ_ENCODING_ZIPLIST) {
    // Add elements to ziplist compressed list
    ...
} else if (zobj->encoding == OBJ_ENCODING_SKIPLIST) { // Add elements to the jump table
    zset *zs = zobj->ptr;
    zskiplistNode *znode;
    dictEntry *de;
    // todo: Look for the specified element in the dictionary. Note that the dictionary is the dictionary structure in the zset structure.
    de = dictFind(zs->dict, ele);
    if (de != NULL) {
        // If the NX mode is turned on and the element already exists in the ordered set, it is returned directly
        /* NX? Return, same element already exists. */
        if (nx) {
            *flags |= ZADD_NOP;
            return 1;
        }
        // Getting the scores of elements in an ordered set in a dictionary
        curscore = *(double *) dictGetVal(de);

        /* Prepare incremental scores if necessary.*/
        if (incr) {
            // Incremental score
            score += curscore;
            if (isnan(score)) {
                *flags |= ZADD_NAN;
                return 0;
            }
            if (newscore) *newscore = score;
        }

        /* Delete and reinsert when the score changes.*/
        if (score != curscore) {
            ...
            // Reinsert elements and values into the jump table
            znode = zslInsert(zs->zsl, score, node->ele);
            // Release node nodes, because we can reuse znode nodes returned by zslInsert to save memory space
            node->ele = NULL;
            zslFreeNode(node);
           // Delete interference code
            ...
        }
        return 1;
    } else if (!xx) {// Operations are performed not only when the element already exists
        // Reproduce the elements in an ordered set
        ele = sdsdup(ele);
        // Direct insertion of elements
        znode = zslInsert(zs->zsl, score, ele);
        // Keys-values consisting of elements in ordered sets and score s are stored in a dictionary in the zset structure
        serverAssert(dictAdd(zs->dict, ele, &znode->score) == DICT_OK);
        ...
    } else {
        ...
    }
} else {
    serverPanic("Unknown sorted set encoding");
}
return 0; /* Never reached. */

}
Everyone is patient to see if there is a little excitement here, because we are about to see how the jump table adds elements, less nonsense, code.

/*

• Add an element to the jump table
  */

zskiplistNode zslInsert(zskiplist zsl, double score, sds ele) {

// Once the length of C language array is determined, no modification is allowed.
// Here it points to the same element as in the level.
zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
// Hierarchical pointer
unsigned int rank[ZSKIPLIST_MAXLEVEL];
int i, level;

serverAssert(!isnan(score));
x = zsl->header;
for (i = zsl->level - 1; i >= 0; i--) {
    /* store rank that is crossed to reach the insert position Insert characters into the specified position*/
    rank[i] = i == (zsl->level - 1) ? 0 : rank[i + 1];
    // todo: Compare the length of the string based on the score, if the score is the same.
    // We know that the elements in an ordered set are ordered, so there must be a sort rule.
    while (x->level[i].forward &&
           (x->level[i].forward->score < score ||
            (x->level[i].forward->score == score &&
             // strcmp() is compared in binary form, without considering multi-byte or wide-byte characters
             sdscmp(x->level[i].forward->ele, ele) < 0))) {
        rank[i] += x->level[i].span;
        x = x->level[i].forward;
    }
    update[i] = x;
}
/*
 * Let's assume that the element is not inside, because we allow repeated scores, and re-inserting the same element should never happen.
 * If the element is internal, the caller of zslInsert () should test in the hash table whether it is already inside or not. You can go back and see the logic of the above method.
 */

// Using Power Law to Calculate the Hierarchy of Nodes
level = zslRandomLevel();
// If the calculated level is higher than the current jump table level
if (level > zsl->level) {
    for (i = zsl->level; i < level; i++) {
        // Here, pointers beyond the original level of zsl are pointed to the new node o
        rank[i] = 0;
        update[i] = zsl->header;
        update[i]->level[i].span = zsl->length;
    }
    zsl->level = level;
}
// Create a jump table node
x = zslCreateNode(level, score, ele);
for (i = 0; i < level; i++) {
    // Chain connection
    x->level[i].forward = update[i]->level[i].forward;
    update[i]->level[i].forward = x;

    /* update span covered by update[i] as x is inserted here  The update scope is overwritten by update [i], because x is inserted here */
    x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
    update[i]->level[i].span = (rank[0] - rank[i]) + 1;
}

/* increment span for untouched levels Increase span*/
for (i = level; i < zsl->level; i++) {
    update[i]->level[i].span++;
}

/* Update Back Pointer */
x->backward = (update[0] == zsl->header) ? NULL : update[0];
if (x->level[0].forward)
    x->level[0].forward->backward = x;
else
    zsl->tail = x;
zsl->length++;
return x;

}
Code see here, you combined with the above jump table to introduce graphic combination, understanding should be faster, if you have any questions, you can leave me a message, I will reply to you in the first time.

zrem command (delete element)
After looking at how to add elements, let's see how redis deletes elements.

void zremCommand(client *c) {

// Ordered sets are returned directly if they do not exist
...
// We know that zrem can delete more than one element at a time. Here we see that redis is a circular deletion element.
for (j = 2; j < c->argc; j++) {
    // Delete the specified element
    if (zsetDel(zobj, c->argv[j]->ptr)) deleted++;
    // If there are no elements in the set, the ordered set is removed directly from the dictionary.
    if (zsetLength(zobj) == 0) {
        dbDelete(c->db, key);
        keyremoved = 1;
        break;
    }
}

// Delete interference code
...

}
Like the method just added, other deletion methods are called to continue looking down.

int zsetDel(robj *zobj, sds ele) {

// If the encoding format is ziplist, delete elements from ziplist
if (zobj->encoding == OBJ_ENCODING_ZIPLIST) {
    ...
} else if (zobj->encoding == OBJ_ENCODING_SKIPLIST) {// The encoding format is a jump table
    zset *zs = zobj->ptr;
    dictEntry *de;
    double score;
    // Remove the element node in the dictionary, but do not release the memory of the node, which will be released in skiplist below.
    de = dictUnlink(zs->dict, ele);
    if (de != NULL) {
        /* Get the score in order to delete from the skiplist later. */
        score = *(double *) dictGetVal(de);

        /* We know that elements and scores are constructed into entries in ordered sets and stored in dictionaries, so we release entries. */
        dictFreeUnlinkedEntry(zs->dict, de);

        /* Release elements in jump tables */
        int retval = zslDelete(zs->zsl, score, ele, NULL);
        serverAssert(retval);

        if (htNeedsResize(zs->dict)) dictResize(zs->dict);
        return 1;
    }
} else {
    serverPanic("Unknown sorted set encoding");
}
return 0; /* No such element found. */

}
So far as the code goes, we should be able to guess what the zslDelete method actually does. Come on, let's guess.

First, locate the element to be deleted in the jump table.

We know that each layer of the node has a precursor and successor pointer, so when we delete this node, we naturally have to change the pointer direction of each layer of the node.

We know that there is a concept of span in redis jump table. If the node is missing, the span of the related node must be changed.

We also know that the jump table is orderly, there is a rank ranking concept, delete a node, the latter node ranking must be changed accordingly.

The node has been deleted, and finally the node space must be released.

We've finished the analysis above. Is it the same as we expected? Let's look at the code.

int zslDelete(zskiplist zsl, double score, sds ele, zskiplistNode *node) {

zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
int i;

x = zsl->header;
// Find the node to update
for (i = zsl->level - 1; i >= 0; i--) {
    while (x->level[i].forward &&
           (x->level[i].forward->score < score ||
            (x->level[i].forward->score == score &&
             sdscmp(x->level[i].forward->ele, ele) < 0))) {
        x = x->level[i].forward;
    }
    update[i] = x;
}
/* We may have multiple elements with the same score, what we need
 * is to find the element with both the right score and object. */
x = x->level[0].forward;
if (x && score == x->score && sdscmp(x->ele, ele) == 0) {
    // Delete skiplistNode node
    zslDeleteNode(zsl, x, update);
    if (!node)
        // Release Node Space
        zslFreeNode(x);
    else
        *node = x;
    return 1;
}
return 0; /* not found */

}
Let's see how redis deletes elements from jump tables

/*

• Internal function used by zslDelete, zslDeleteByScore and zslDeleteByRank
• This method modifies the span in the jump table
  *
• Internal functions used by zslDelete, zslDeleteByScore and zslDeleteByRank
  */

void zslDeleteNode(zskiplist zsl, zskiplistNode x, zskiplistNode **update) {

int i;
for (i = 0; i < zsl->level; i++) {
    if (update[i]->level[i].forward == x) {
        update[i]->level[i].span += x->level[i].span - 1;
        update[i]->level[i].forward = x->level[i].forward;
    } else {
        // Computational span
        update[i]->level[i].span -= 1;
    }
}
if (x->level[0].forward) {
    x->level[0].forward->backward = x->backward;
} else {
    zsl->tail = x->backward;
}
while (zsl->level > 1 && zsl->header->level[zsl->level - 1].forward == NULL)
    zsl->level--;
zsl->length--;

}
zscore command (get element score)
We can think about getting the score of a certain value. In the jump table, do we need to find the designated node in the jump table first and then get the score of that node? With that in mind, let's look at the source code.

/**

• zscore
• @param c
  */

void zscoreCommand(client *c) {

robj *key = c->argv[1];
robj *zobj;
double score;
// If the ordered set or element type is not OBJ_ZSET found in the dictionary, return directly
if ((zobj = lookupKeyReadOrReply(c, key, shared.nullbulk)) == NULL ||
    checkType(c, zobj, OBJ_ZSET))
    return;
// Get the score
if (zsetScore(zobj, c->argv[2]->ptr, &score) == C_ERR) {
    addReply(c, shared.nullbulk);
} else {
    addReplyDouble(c, score);
}

}
From the above, we can see that the score is actually obtained through the zsetScore method.

int zsetScore(robj zobj, sds member, double score) {
if (!zobj || !member) return C_ERR;
// If the encoding format compresses the linked list
if (zobj->encoding == OBJ_ENCODING_ZIPLIST) {

   if (zzlFind(zobj->ptr, member, score) == NULL) return C_ERR;

} Other if (zobj - > encoding = OBJ_ENCODING_SKIPLIST) {// The encoding format is a jump table

   zset *zs = zobj->ptr;
   // Get the specified dictEntry directly from the dictionary in zset
   dictEntry *de = dictFind(zs->dict, member);
   if (de == NULL) return C_ERR;
   // Getting score from dictEntry
   *score = *(double *) dictGetVal(de);

} else {

   serverPanic("Unknown sorted set encoding");

}
return C_OK;
}
zrank command (get the rank of an element)
When we want to get the ranking of an element in an ordered set, the zrank command is a good choice for us. The zrank command returns the ranking of members in the ordered set key. The ordered integrators are arranged in the order of increasing score value (from small to large). The bottom ranking is zero, that is to say, members with the smallest Score Rank zero. Now let's see how it works out in him.

long zsetRank(robj *zobj, sds ele, int reverse) {

unsigned long llen;
unsigned long rank;

llen = zsetLength(zobj);

if (zobj->encoding == OBJ_ENCODING_ZIPLIST) {
    // Compressed list rank calculation method
    ...
} else if (zobj->encoding == OBJ_ENCODING_SKIPLIST) {
    zset *zs = zobj->ptr;
    zskiplist *zsl = zs->zsl;
    dictEntry *de;
    double score;
    // Get the specified element dictEntry directly from the dictionary in zset
    de = dictFind(zs->dict, ele);
    if (de != NULL) {
        score = *(double *) dictGetVal(de);
        rank = zslGetRank(zsl, score, ele);
        /* Existing elements always have a rank. */
        serverAssert(rank != 0);
        if (reverse)
            return llen - rank;
        else
            return rank - 1;
    } else {
        return -1;
    }
} else {
    serverPanic("Unknown sorted set encoding");
}

}
Next is the real rank calculation method. Don't be distracted, concentrate on it.

unsigned long zslGetRank(zskiplist *zsl, double score, sds ele) {

zskiplistNode *x;
unsigned long rank = 0;
int i;

x = zsl->header;
// Here we start at the top to find the ranking of node elements
for (i = zsl->level - 1; i >= 0; i--) {
    while (x->level[i].forward &&
           (x->level[i].forward->score < score ||
            (x->level[i].forward->score == score &&
             sdscmp(x->level[i].forward->ele, ele) <= 0))) {
        rank += x->level[i].span;
        x = x->level[i].forward;
    }

    /* x might be equal to zsl->header, so test if obj is non-NULL */
    if (x->ele && sdscmp(x->ele, ele) == 0) {
        return rank;
    }
}
return 0;

}
Well, here's the implementation of the jump table in Redis.

Reference article: Redis Jump Table