Title Source:
POJ http://poj.org/problem?id=1177
HDU : http://acm.hdu.edu.cn/showproblem.php?pid=1255
It's really Cai. After watching the scan line for a day, I blogged and talked.
Scan line:
Scanning lines are commonly used on graphics to solve problems with perimeter areas (such as giving you a lot of rectangular positions, asking them for their total area, and noting that rectangles can overlap here, so the problem becomes more complex). The idea of scanning lines arises from this?
As the name implies, a line (parallel to the x- or y-axis) is scanned from beginning to end in a coordinate system, as shown in the following example
Now there are two rectangles as shown in the picture below. How do I find their perimeters with the scanning lines?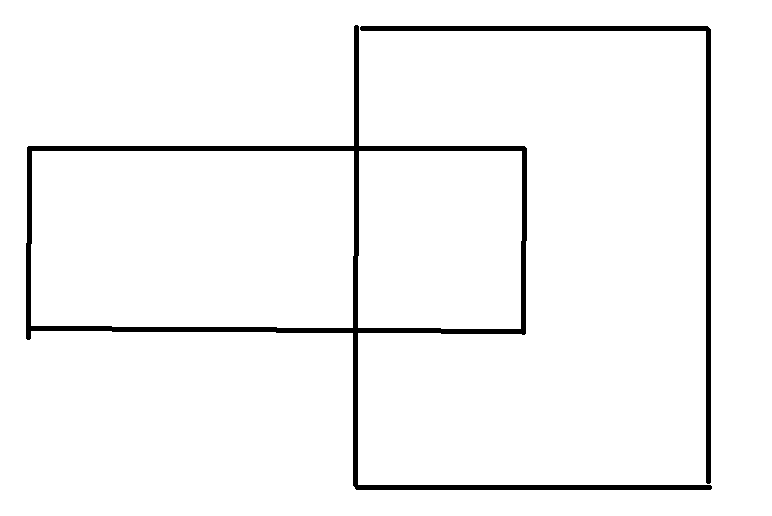
We can scan this graph with a line parallel to the x-axis and y-axis, respectively. For example, with a line parallel to the y-axis, the position of the line is not arbitrary, but coincides exactly with one side of the rectangle. Sweep from left to right as follows
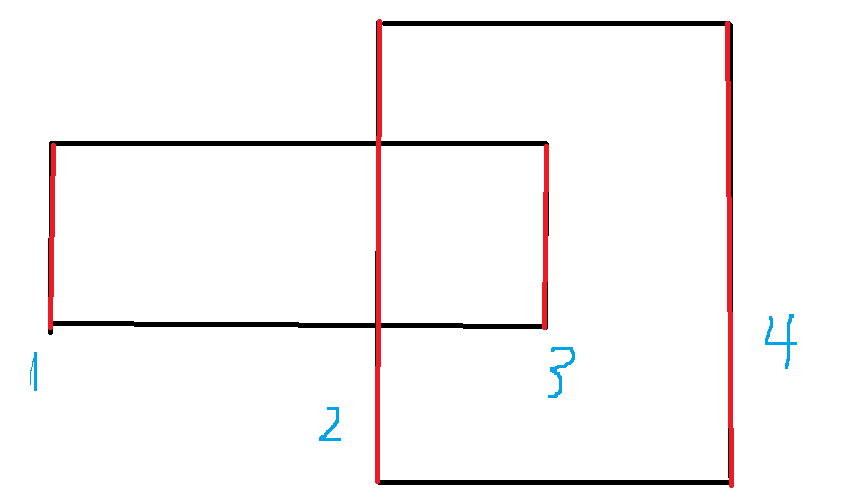
We just add up the y-axis (the difference in the length of the area covered by the front and back segments) each time (when taking 12,334) to get the perimeter of the y-axis direction.There are also operations involved, such as marking the left segment of the rectangle as 1 and the right segment as -1.
From the beginning, the first 1 covers the length plus 1;
By 2, add 2 coverage areas - 1 coverage area length
When 3 is reached, the area covered by 1 is cancelled out by 3 (mark 1-1), and the area covered by 3 is 0
And finally 4, because 3 doesn't cover it, just add 4's
This is the whole process. Let's not say more about the other half. Let's look at two examples~
Actual Warfare:
POJ 1177 Picture


Ideas:
This question is similar to what is explained in the explanation. It is OK to scan lines twice and maintain them through a segment tree.
Also note that instead of recursing to L R here, l+1r because l==r doesn't make sense here
Code:
#include<iostream> #include<algorithm> #include<cstdio> #include<cstring> using namespace std; const int maxn=2e4+5; const int mod=1e9+7; typedef long long ll; int n,m; int sum[maxn<<2],add[maxn<<2]; struct node { int l,r,h,flag; }line1[maxn<<1],line2[maxn<<1]; bool cmp(node a,node b) { if(a.h!=b.h) return a.h<b.h; return a.flag>b.flag; } void build(int k,int l,int r) { sum[k]=0; add[k]=0; if(l+1==r) return ; int mid=l+r>>1; build(k<<1,l,mid); build(k<<1|1,mid,r); } void pushup(int k,int l,int r) { if(add[k]){ sum[k]=r-l; } else if(l+1==r){ sum[k]=0; } else{ sum[k]=sum[k<<1]+sum[k<<1|1]; } } void update(int k,int l,int r,int x,int y,int flag) { // cout<<l<<' '<<r<<endl; if(x<=l&&r<=y){ add[k]+=flag; pushup(k,l,r); return ; } int mid=l+r>>1; if(mid>x) update(k<<1,l,mid,x,y,flag); if(mid<y) update(k<<1|1,mid,r,x,y,flag); pushup(k,l,r); } int main() { int n; while(~scanf("%d",&n)){ int x1,y1,x2,y2; build(1,1,20005); for(int i=1;i<=n;i++){ scanf("%d%d%d%d",&x1,&y1,&x2,&y2); x1+=10001; x2+=10001; //This question has negative coordinates, which is strange to see, so add them all to 10001 and make them positive. y1+=10001; y2+=10001; line1[i].l=x1; line1[i].r=x2; line1[i].h=y1; line1[i].flag=1; line1[i+n].l=x1; line1[i+n].r=x2; line1[i+n].h=y2; line1[i+n].flag=-1; line2[i].l=y1; line2[i].r=y2; line2[i].h=x1; line2[i].flag=1; line2[i+n].l=y1; line2[i+n].r=y2; line2[i+n].h=x2; line2[i+n].flag=-1; } sort(line1+1,line1+n*2+1,cmp); sort(line2+1,line2+n*2+1,cmp); int ans=0; for(int i=1;i<=2*n;i++){ int temp=sum[1]; update(1,1,20005,line1[i].l,line1[i].r,line1[i].flag); ans+=abs(sum[1]-temp); // cout<<line1[i].l<<' '<<line1[i].r<<' '<<line1[i].h<<' '<<ans<<endl; } build(1,1,20005); for(int i=1;i<=2*n;i++){ int temp=sum[1]; update(1,1,20005,line2[i].l,line2[i].r,line2[i].flag); ans+=abs(sum[1]-temp); // cout<<ans<<endl; } cout<<ans<<endl; } return 0; } // 1 20 - 4 9 // 1 10 4
Area Covered by HDU 1255
Learn from https://blog.csdn.net/w326159487/article/details/77714912

Ideas:
First, the question has decimals, and the first step is to discretize it, using the unique function in the STL Library
And then for the area covered, let's think, if there are only two rectangles, and there is a common area between them
Or use the picture above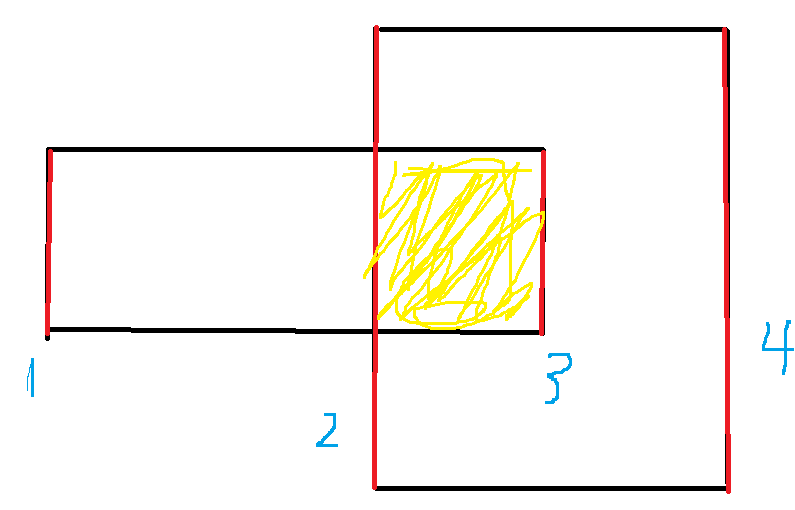
When looping to the second edge, the area of 1 has been covered twice, and the length of the covered area is equal to the area covered by x of the next edge minus x of this edge and multiplied by x of this covered area.We can also use this method when we think about a number of things, because if there is a common area, there will be two overlays and then the right side of the rectangle with the overlay will appear.
Code:
#include<iostream> #include<algorithm> #include<cstdio> #include<cstring> using namespace std; const int maxn=2e3+5; const int mod=1e9+7; typedef long long ll; int n,m; double sum[maxn<<3],lvl[maxn<<1]; int cover[maxn<<3]; struct node { double x,y1,y2; int in; //Record left and right markers node(double a,double b,double c,int d) {x = a; y1 = b; y2 = c; in = d;} //Class-like constructors node(){} }f[maxn]; bool cmp(node a,node b){return a.x<b.x;} int getval(double val) {return lower_bound(lvl+1,lvl+m+1,val)-lvl;} //Binary Find val Location void update(int k,int cc,int l,int r,int x,int y) { if(l+1==r){ cover[k]+=cc; sum[k]=cover[k]>1?lvl[r]-lvl[l]:0; return ; } int mid=l+r>>1; if(mid>x) update(k<<1,cc,l,mid,x,y); if(mid<y) update(k<<1|1,cc,mid,r,x,y); sum[k]=sum[k<<1]+sum[k<<1|1]; } int main() { int t; scanf("%d",&t); while(t--){ memset(sum,0,sizeof sum); memset(cover,0,sizeof cover); scanf("%d",&n); for(int i=1;i<=n;i++){ double a,b,c,d; scanf("%lf%lf%lf%lf",&a,&b,&c,&d); lvl[i*2-1]=b; lvl[i*2]=d; f[i*2-1]=node(a,b,d,1); f[i*2]=node(c,b,d,-1); } sort(f+1,f+2*n+1,cmp); sort(lvl+1,lvl+2*n+1); m=unique(lvl+1,lvl+2*n+1)-lvl-1; //Duplicate removal double ans=0; // cout<<m<<endl; update(1,f[1].in,1,m,getval(f[1].y1),getval(f[1].y2)); //First time to preprocess, no duplicate area is possible for the first time for(int i=2;i<=2*n;i++){ ans+=(f[i].x-f[i-1].x)*sum[1]; // cout<<sum[1]<<endl; update(1,f[i].in,1,m,getval(f[i].y1),getval(f[i].y2)); } printf("%.2f\n",ans); } }