Using KMP algorithm to implement str ()

One topic
From leetcode official website

Here are two strings, haystack and need. Please find the first position where the need string appears in the haystack string (the subscript starts from 0). If it does not exist, it returns - 1.
Note: when the need is an empty string, we should return 0. This is consistent with the C language's str () and Java's indexOf() definitions.
II. Violent cracking method

For this problem, you can use the brute force method. As shown in the above figure, compare the first character of need with the character in haystack in turn. If it is not equal, replace it with the second character in haystack. If it is equal, compare the second character of need with the next character of haystack comparison character. If all characters in the need have been compared and equal to the relative position of haystack, the answer is found.
code:

class Solution {
    public int strStr(String haystack, String needle) {
        int index = -1;
        if(needle.isBlank()){
            index = 0;
        } else {
            char[] hay = haystack.toCharArray();
            char[] need = needle.toCharArray();
            for(int i = 0;i<hay.length;i++){
                int j=0, tmp = i;
                while (j<needle.length()&&tmp<hay.length&&hay[tmp]==need[j]){
                    tmp++;
                    j++;
                }
                if(j>=needle.length()){
                    index=i;
                    break;
                }
            }
        }
        return index;
    }
}

Operation results:
The operation efficiency is too low.

Third, KMP algorithm is used to solve
KMP algorithm is an improved string matching algorithm. The core idea is to create a fallback array next for the need string according to the public prefix
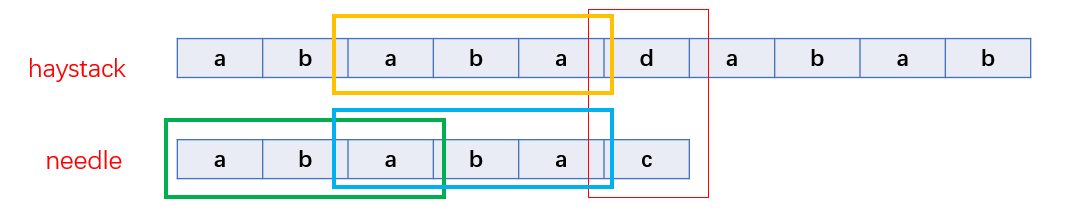
As shown in the following figure: to the red box, the string need does not match haystack. According to the brute force method, you should start with the second character of haystack string and re compare it with the first character of need. However, by observing these two strings, we can see that the characters in the orange box match the characters in the blue box, and for the characters before C, the strings in the blue box are equal to those in the green box. Therefore, it can be equivalent to that the orange box has been compared with the green box. At this time, we can compare the next character of the orange box with the next character of the green box. If they are equal, the characters continue to move down. If they are not equal, they will find a matching string again. In order to know where we should go back to the need string every time there is a mismatch, we create a next array for the need string.
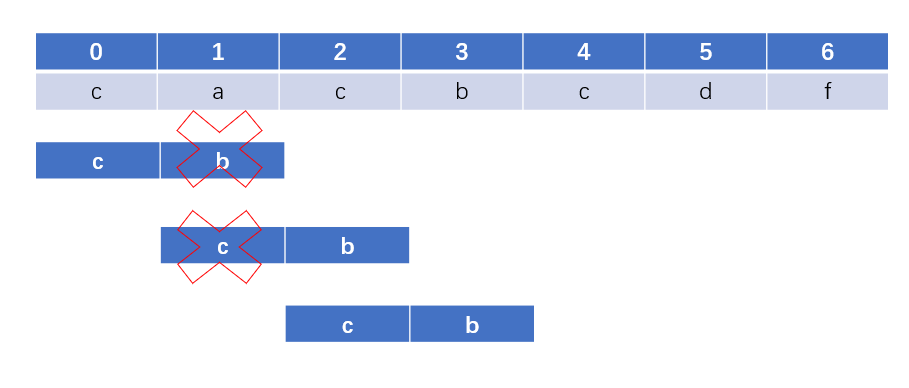
The next array is int[] next, the index of the array is the needle string index, and the value is the position that should be fallback. Convert the need into a character array. For the need [i], the position that can be fallback is the position of the largest public pre suffix + 1 after the need [0] to the need [I-1]. For the need shown in the figure below, for the position of the c string, the need [0] to need [I-1] are aba, the prefixes are: A, AB, aba, aba, and the suffixes are: baba,aba,ba,a. therefore, the maximum common pre suffix is aba. next[5]=3.
For the next array, there are two characteristics if the maximum value of need [J + 1] is next[j]+1 If next[j+1] is not equal to need [next[j]+1], the maximum possible value of next[j+1] is next[next[j]]+1. And so on. You can get the next array.

class Solution {
    public int strStr(String haystack, String needle) {
        int index = -1;
        if(needle.isBlank()){
            index = 0;
        } else {
            int[] next = new int[needle.length()];
            createNext(next,needle);
            int i = 0;
            int j =0;
            while (j<needle.length() && i<haystack.length()){
                if(haystack.charAt(i)==needle.charAt(j)){
                    i++;
                    j++;
                }else{
                    j=next[j];
                    if(j==-1){
                        i++;
                        j++;
                    }
                }
            }
            if(j>=needle.length()){
                index = i-j;
            }
        }
        return index;
    }
    private void createNext(int[] next,String needle){
        char[] tmp = needle.toCharArray();
        next[0] = -1;
        int i = 0,j=-1;
        while(i<needle.length()-1){
            if(j==-1 || tmp[i]==tmp[j]){
                next[++i]=++j;
            }else{
                j=next[j];
            }
        }
    }
}

Operation results: