catalog

2, Introduction to 2D array

2.1 rotation matrix

2.2 zero matrix

2.3 diagonal traversal ☆

2, Introduction to 2D array

2.1 rotation matrix

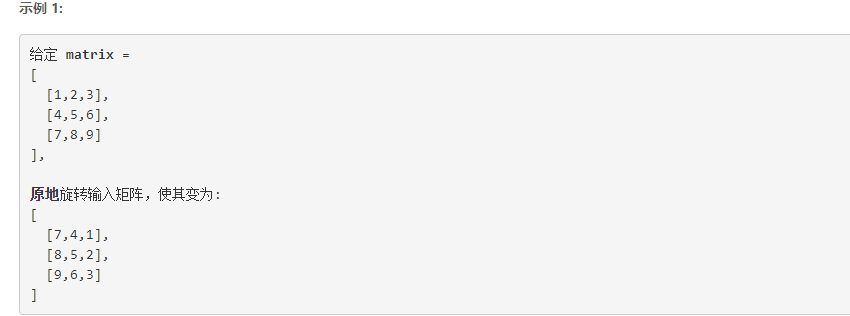
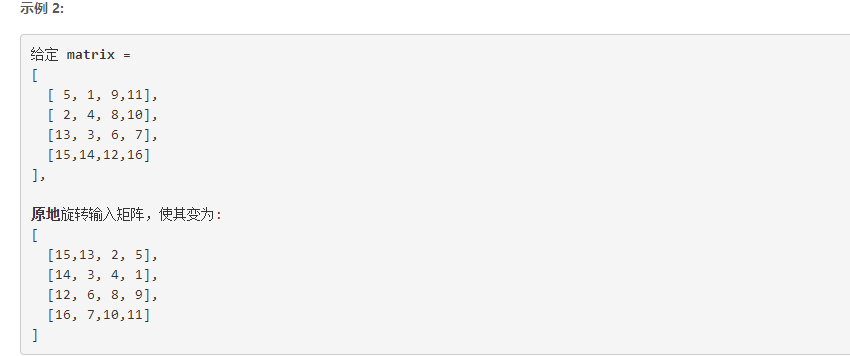
2.1.1 problem description

2.1.2 solution process

Method 1: no additional space is allowed, so you can only operate in place. In other words, each transformation must be completed once and cannot be accessed again. For this purpose, you can choose to rotate 90 ° clockwise for four corresponding position elements at a time from the outer layer to the inner layer. The number of circulation floor s is determined by rounding up n/2. The complexity is determined by rounding up n*n/4, which is O(n^2)

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        # Adjust 4 pieces at a time, total n*n/4 up rounding
        n = len(matrix)
        if n <= 1:
            return matrix
        
        #quo, rem = divmod(n, 2)
        #floor = quo + rem
        floor = sum(divmod(n, 2))  # From outside to inside, processing layers
        # i is the starting index of each layer, for example, the outermost layer starts from [0] [0] for the first time, and the second layer starts from [1] [1]
        for i in range(floor):  # Number of layers
            limit = n-i-1  # Upper index limit of current layer
            k = 0  # index adjust auxiliary variable
            for j in range(i, limit):  # Adjust the positions of 4 elements clockwise at the same time each time
                matrix[i][j], matrix[j][limit], matrix[limit][limit-k], matrix[limit-k][i] = \
                matrix[limit-k][i], matrix[i][j], matrix[j][limit], matrix[limit][limit-k]
                k += 1   
        return matrix

2.2 zero matrix

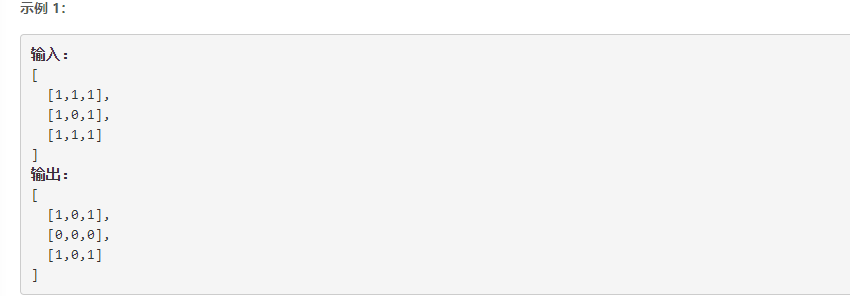
2.2.1 problem description

2.2.2 solution process

Method 1: simple / violent method, the first traversal is used to find and record 0 elements, the second traversal is used to clear the row elements, and the third traversal is used to clear the column elements. It is inefficient because it contains many redundant operations. Complexity O(n^2).

In addition, using list derivation is better than [0]*x, because you can avoid each row of 0 pointing to the same 0 list object! (although this topic does not reflect the harmfulness)

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        if (len(matrix) <= 1) and (0 not in matrix[0]):  # Special case [[0,1]]
                pass
        else:
            zero_row = set()  # Save the abscissa of the 0 element
            zero_col = set()  # Save the ordinates of the 0 element
            # Search and record zero
            for i, row in enumerate(matrix):
                for j, num in enumerate(row):
                    if num == 0:
                        zero_row.add(i)
                        zero_col.add(j)
            # Line clearing                 
            for r_i in zero_row:
                matrix[r_i] = [0 for _ in range(len(matrix[0]))]  
            # Column zeroing
            for c_j in zero_col:
                for k in range(len(matrix)):
                    matrix[k][c_j] = 0

Method 2: simple method to optimize I. Add hasZero as a Flag to identify whether the current line has zero. If there is one, the whole line will be cleared directly after traversing the line. It is unnecessary to open another for loop to specifically clear the line. But the column is not good, because it is uncertain whether a new column index will be added, so a new for loop must be opened to clear the column. Complexity O(n^2).

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        if (len(matrix) <= 1) and (0 not in matrix[0]):  # Special case [[0,1]]
            pass
        else:
            zero_col = set()  # Save the ordinates of the 0 element
            # Search and record zero
            for i, row in enumerate(matrix):
                hasZero = False
                for j, num in enumerate(row):
                    if num == 0:
                        zero_col.add(j)  # 0 element ordinate
                        hasZero = True
                if hasZero:
                    matrix[i] = [0 for _ in range(len(matrix[0]))]  # Clean up 
            # Column zeroing
            for c_j in zero_col:
                for k in range(len(matrix)):
                    matrix[k][c_j] = 0

Method 3: simple method optimization II. Add zero again_ Row is used to store row index without 0, so as to combine zero_column implements the processing of the remaining 0. Complexity O(n^2).

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        if (len(matrix) <= 1) and (0 not in matrix[0]):  # Special case [[0,1]]
            pass
        else:
            zero_row = set()  # Save row index without 0 element
            zero_col = set()  # Save the ordinates of the 0 element
            # Search and record 0
            for i, row in enumerate(matrix):
                hasZero = False  # This bank has 0 flag
                for j, num in enumerate(row):
                    if num == 0:
                        zero_col.add(j)  # 0 element ordinate
                        hasZero = True
                if hasZero:
                    matrix[i] = [0 for _ in range(len(matrix[0]))]  # Zero in this line, clear the whole line directly 
                else:
                    zero_row.add(i)  # No 0 in this line, record line index for subsequent cleaning       
            # Clear the rest of the elements
            for r_i in zero_row:
                for c_j in zero_col:
                    matrix[r_i][c_j] = 0

2.3 diagonal traversal

2.3.1 problem description

2.2.2 solution process (☆)

Method 1 (intuitionistic method / naive method): in the example, the input range of two-dimensional array is 0-2. Let's first observe the ergodic Law: (0, 0) → (0, 1) → (1, 0) → (2, 0) → (1, 1) → (0, 2) → (1, 2) → (2, 1) → (2, 2). If the array index is (m, n), there are two ways to change the index: (m-1, n+1) or (m+1, n-1).

The array starts from (0,0) and the index changes in the way of (m-1, n+1), i.e. (0, 0) → (- 1, 1) (i.e. 0-1 = - 1, 0 + 1 = 1), but the abscissa m = -1 is out of the range (0 ~ 2), let m = 0 (to be within the range of 0 ~ 2) to get the starting point of the next traverse (0, 1).

Then, switch the index change mode to (m+1, n-1), execute (0, 1) → (1, 0) → (2, - 1) successively, but at this time, the ordinate n=-1 is out of the range (0 ~ 2), similarly, let n = 0 (to be within the range of 0 ~ 2) to get the starting point of the next traverse (2, 0).

Switch the index change mode to (m-1, n+1) again, execute (2, 0) → (1, 1) → (0, 2) → (- 1, 3) successively until it is out of range (0 ~ 2). However, the difference is that m < 0 and N > 2 are out of range. At this time, we should first determine whether n is out of range, and then, in particular, execute (m+2, n-1) implementation (- 1,3) → (1,2), to avoid switching the index change mode again due to m < 0.

Then, the index change mode switches back to (m+1, n-1) normally, and executes (1, 2) → (2, 1) → (3, 0) successively. Because m > 2 is out of range, execute (m-1, n+2) specially to realize (3, 0) → (2, 2) traversal.

It can be seen that two normal traversal directions (top right and bottom left) correspond to two index change modes respectively; four special cases (horizontal and vertical coordinates exceeding top and next) correspond to four index correction modes respectively, and adjust the traversal direction at the same time. Complexity O(n)

class Solution:
    def findDiagonalOrder(self, matrix: List[List[int]]) -> List[int]:
        # Special case handling mechanism
        if not matrix:  # matrix = []
            return []
        
        col = len(matrix)  # Lines / ordinate Max
        row = len(matrix[0])  # Number of columns / maximum abscissa
        nums = col * row  # Total elements
        m = 0  # Starting point abscissa index
        n = 0  # Starting point ordinate index
        flag = True  # Used to determine coordinate transformation mechanism (m-1, n+1) or (m+1, n-1)
        res = []  # Initializing the list of diagonal traversal elements
        
        # Start diagonal traversal of all elements in the matrix
        for i in range(nums):
            # Include element
            res.append(matrix[m][n])
            # Normal traversal
            if flag:        # Coordinate transformation mechanism (m-1, n+1)
                m -= 1
                n += 1
            else:           # Coordinate transformation mechanism (m+1, n-1)
                m += 1
                n -= 1
            # Special case correction    
            if m >= col:    # If the abscissa m is greater than the range, one time order (m-1, n+2)
                m -= 1
                n += 2
                flag = True
            elif n >= row:  # If the ordinate n is greater than the range, one time order (m+2, n-1)
                m += 2
                n -= 1
                flag = False
            if m < 0:       # If the abscissa m is less than the range, let m=0 at one time
                m = 0
                flag = False
            elif n < 0:     # If the ordinate n is less than the range, let n=0 at one time
                n = 0
                flag = True
                
        return res

Method 2: the same unknown principle. The former uses nested list to add elements; the latter uses defaultdict to add elements, so the efficiency is the highest!

class Solution:
    def findDiagonalOrder(self, matrix: List[List[int]]) -> List[int]:
        # Special case handling
        if not matrix:
            return []
        row = len(matrix)  # Lines / ordinate Max
        col = len(matrix[0])  # Number of columns / maximum abscissa
        l = row + col - 1  # Total elements - 1
        # Using list derivation to generate empty nested list as auxiliary table
        rets = [[] for _ in range(l)]  # Faster and safer than [[] * l]!
        
        for i in range(row):
            for j, num in enumerate(matrix[i]):
                rets[i+j].append(num)
        print(rets)
        # Initialize output results
        ret = []
        for k, x in enumerate(rets):
            ret += x if (k % 2 == 1) else x[::-1]  # One line, unknown principle
            print(ret)
        return ret
# -------------------------------------------------------------------------------
class Solution:
    def findDiagonalOrder(self, matrix: List[List[int]]) -> List[int]:
        # Special case handling
        if not matrix: 
            return []
        
        # Construct default list dictionary
        dic = collections.defaultdict(list)
        # Add elements according to the sum of index
        for i in range(len(matrix)):
            for j in range(len(matrix[0])):
                dic[i+j].append(matrix[i][j])
        print(dic)
        
        # Initialize output results
        res = []
        for i in range(len(matrix)+len(matrix[0])-1):
            if i%2==0:
                res += dic[i][::-1]
            else:
                res += dic[i]
            print(res)
        return res