Description of the problem:

Store n(n>1) integers in a one-dimensional array R, and design an algorithm that is as efficient as possible in both time and space. Move the sequence loop stored in R to the left of p(0<p<n) positions, i.e., transform the data in R (x0,x1,x2,... x(n-1)) to (x p, x(p+1),..., x(n-1),x0,x1,..., x(p-1))

Example:

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

Move left 4 bits

[5, 6, 7, 8, 9, 10, 1, 2, 3, 4]

Intermediate Array Auxiliary Method

Solution ideas: Define an intermediate array temp[] to assist elements of the R[] array in moving.

1. Looking at the reverse method of the code below, there are three for loops. These three for loops are the core code of the algorithm to move elements to the left.

Assuming the array R = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10], move 4 bits to the left (p = 4)

1. The first for loop: temporarily stores the first p elements in the array R into the temp array.
   
2. Second for loop: move the last n-p elements in the array R to the left by p. (Actually, left shift is not appropriate here, it should be said: assign the value of the last n-p elements to the first n-p elements.)
   
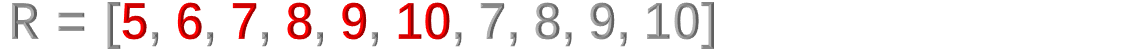
3. Third for loop: temp elements are temporarily present in the first for loop, and sequentially assigned to the next p elements in the R array
   

public class Solution_3 {

    public static void reverse(int[] R, int p) {
        //Intermediate Array
        int[] temp = new int[R.length];

        //Temporarily store the first p elements in the R array into the temp array
        for (int i = 0; i < p; i++) {
            temp[i] = R[i];
        }

        //Move the last n-p elements in the R array to the left by p as a whole
        for (int i = p; i < R.length; i++) {
            R[i-p] = R[i];
        }

        //The elements that are temporarily present in the temp array are assigned sequentially to the next p elements in the R array
        int start = 0;
        for (int i = R.length-p; i < R.length; i++) {
            R[i] = temp[start++];
        }

    }

    public static void main(String[] args) {
        int[] R = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
        int p = new Scanner(System.in).nextInt();
        reverse(R, p);
        //Print out arrays as strings
        System.out.println(Arrays.toString(R));
    }
}

Space-Time Complexity: The algorithm has only a single-layer loop and the time complexity is O(n), because an intermediate array of length n is opened in external memory, and the space complexity is O(n).

Code optimization: In the previous reverse method, the first and second code can be merged.

Parse: Temporary elements to temp array and steps to move elements of R array to the left are merged into a for loop. However, it is important to note that the first for loop before is to temporarily store p elements directly into the temp array. After merging, n-p elements are temporarily stored in the temp array. Because n-p elements in the R array need to be moved to the left.

for (int i = 0; i < R.length-p; i++) { // T(n) = 3n = O(n)
    //Temporarily store the first n-p elements in the R array into the temp array
    temp[i] = R[i];
    //Assign the last n-p elements of the R array to the previous n-p elements
    R[i] = R[i + p];
}

Space-time complexity: This step does not reduce the time complexity of the algorithm, or O(n). It just reduces the amount of code.

Array Element Inversion

Solve the problem by dividing the R array into a and b parts, then inverting the elements of a and b parts respectively, and then inverting the R array as a whole. So we need to invoke the element inversion algorithm three times.

public class Solution_2 {

    private static void reverse(int[] R, int left, int right) {
        //Array Element Interposition Algorithm (actually the interchange of two numbers)
        for(int i = 0; i <= (right - left)/2; i++){
            int temp = R[left + i];
            R[left + i] = R[right - i];
            R[right - i] = temp;
        }
    }

    private static void move(int[] R, int n, int p) {
        //Invert the first part of the array
        reverse(R,0,p - 1);

        //Invert the second part of the array
        reverse(R, p,n - 1);

        //Invert the elements of the entire array
        reverse(R,0,n - 1);
    }

    public static void main(String[] args) {
        int[] R = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
        int p = new Scanner(System.in).nextInt();
        move(R, R.length, p);
        //Print out the array in string format
        System.out.println(Arrays.toString(R));
    }
}

Space-Time Complexity: This algorithm uses a cycle with a time complexity of O(n) because there is little external memory and a space complexity of O(1).