When an array simulates a queue, there will be a problem that it cannot be reused. Here, a ring queue is used to solve the problem.

Because the simulation is a ring queue, let's adjust the meaning of each attribute in the queue.

1. Analysis:

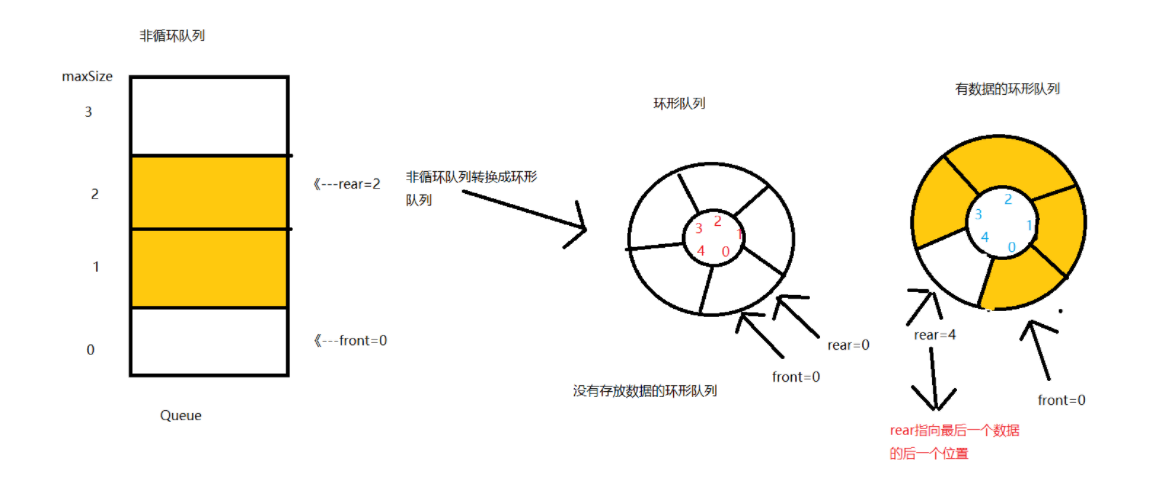
The original acyclic queue (non ring queue) cannot store data when the tail pointer of rear reaches rear==maxSize-1. Even if we take out the data, we only take out the data logically. The real situation is that after the data is taken out, there is still the data in the queue. How should we solve this problem? The answer is - ring queue.

Therefore, we need to improve this queue and change it into a ring queue (circular queue), so that the queue can achieve a reuse effect.

1. The idea of ring queue is that when the rear pointer reaches the maximum capacity of the queue, the rear continues to increase from tail to head and from head to tail, so as to store data circularly.

2. However, it is obviously impossible to judge whether the queue is full according to the condition of acyclic queue (described in the previous array simulation queue) real = = front, because when there is no data at the beginning, real = = front indicates that the queue is empty. However, the ring queue keeps increasing. When the rear keeps increasing to the head, that is, the front, there is data at this time, and the rear is equal to the front. Therefore, according to the conditions of pulmonary circulation queue, it is impossible to determine whether the ring queue (circulation queue) is full.

3. At this time, we make an agreement: we sacrifice a space in the ring queue so that we can judge whether the ring queue is full.

• Because we have reserved a space, the property of rear is adjusted to point to the position of the last element of the queue. That is, real = real + 1 at this time

• The initial value of the property value of real is 0

• The front attribute is adjusted to point to the first element of the queue header.

• The initial value of the front property is 0

• Because the rear is always increasing, we need to take the remainder of maxSize to get a real position of the rear. Therefore, the condition for judging the full queue is (rear+1)%maxSize==front [Full queue]

• The condition of team empty is: rear==front.

• When we analyze this way, the number of valid data in the queue is (rear + maxsize front)% maxsize / / as shown in the figure above: rear=4,maxSize=5,front=0, the number of valid data is: (4 + 5-0)% 5 = = 4, and the number of valid data in the figure above is exactly 4.

• We only need to make changes based on the acyclic queue (non ring queue) code to implement the ring queue.

package com.lzh.queue;

import java.util.Scanner;

public class CircleArrayQueue {
    public static void main(String[] args) {
        //Test -- create a queue
        CircleQueue circleQueue = new CircleQueue(4);
        char key = ' ';//Receive user input
        Scanner scanner = new Scanner(System.in);
        boolean loop = true;
        while (loop) {

            System.out.println("s(show):Show queue");
            System.out.println("e(exit):Exit program");
            System.out.println("a(add):Add data to queue");
            System.out.println("g(get):Fetch data from queue");
            System.out.println("h(head):View data of queue header");
            //key=scanner.next().charAt(0);  Put it in this position
            key = scanner.next().charAt(0); //Receives the first character entered by the user
            switch (key) {
                case 's':
                    circleQueue.showAll();
                    break;
                case 'e' :
                    scanner.close();
                    loop = false;
                    System.out.println("Program exit");
                    break;
                case 'a' :
                    System.out.println("Please enter an integer");
                    int a = scanner.nextInt();
                    circleQueue.addQueue(a);
                    break;
                case 'g' :
                    try {
                        int res = circleQueue.getQueue();
                        System.out.println(res);
                    }catch (Exception e){
                        System.out.println(e.getMessage());
                    }

                    break;
                case 'h' :
                    try{
                        int head = circleQueue.getHead();
                        System.out.println(head);
                    }catch (Exception e){
                        System.out.println(e.getMessage());
                    }
                    break;

            }


        }
    }

}

//Use arrays to simulate ring queues
class CircleQueue{
    //The initial values of front and rear are set to 0
    private int maxSize;//Maximum capacity of the array
    //The default value of front is 0
    private int front;//Points to the first element of the queue
    private int rear;//Points to the next position after the last element of the queue
    private int[] arr;//The array stores data and uses the array to simulate the queue

    //Create a construction method
    public CircleQueue(int arrayMaxSize){
        maxSize = arrayMaxSize;
        arr = new int[maxSize];
        //There is no need to assign values to front and rear, because the default value is 0
    }
    //Determine whether the queue is empty
    public boolean isNull(){
       return rear == front;
    }
    //Determine whether the queue is full of data
    public boolean isFull(){
        return (rear+1)%maxSize == front;
    }
    //Add data to the queue
    public void addQueue(int n){
        //First determine whether the queue is full
        if(isFull()){
            System.out.println("The queue is full,No more data can be added");
            return;
        }
        //If not, execute the following code
        //Because the rear point is the last position of the last element, the position of this place must be empty, so you can add data directly
        arr[rear] = n;
        //After adding, the pointer moves backward, but if it is a ring queue, the subscript may be out of bounds if the rear is added all the time, so modulo is used here
        rear=(rear+1)%maxSize;
    }
    //Fetch data from queue
    public int getQueue(){
        //First judge whether the queue is empty
        if(isNull()){
            throw  new RuntimeException("The queue is empty and data cannot be fetched");
        }
        //Because front is the first element pointing to the queue, you can get it directly
        //Use an intermediate variable to receive the received data, and then move the front backward, otherwise the front cannot move backward
        int value = arr[front];
        //The same is true for front. Increasing all the time will cause the subscript to cross the boundary, so we also do a modular calculation
        front = (front+1)%maxSize;
        return value;
    }
    //Display header data
    public int getHead(){
        //First judge whether the queue is empty
        if(isNull()){
            throw  new RuntimeException("The queue is empty and no header data can be obtained");
        }
        return arr[front];
    }
    //Show all data
    public void showAll(){
        //First judge whether the queue is empty
        if (isNull()) {
            System.out.println("The queue is empty,Data not available");
            return;
        }
        //Here we print out all the data, but we don't need to print the empty position, so let i=front, start with the first element
        //This front+size() represents the subscript of the first element + how many valid elements, replacing the previous range of i
        //For example, if front = = 1, size () = = 3, maxsize = 5, the loop is executed three times
        for (int i = front;i<front+size();i++){
            //Why take the module here? Because i==front, I < front + size() may have the subscript out of bounds, we take the module
            System.out.printf("arr[%d]=%d\n", i%maxSize, arr[i%maxSize]);
        }
    }
    //Get how much valid data the queue has
    public int size(){
        return (rear+maxSize-front)%maxSize;
    }
}