1. Most elements

Title Description:

Given an array of size n, find most of its elements. Most elements refer to elements that appear more than ⌊ n/2 ⌋ in the array.

You can assume that the array is non empty and that there are always many elements in a given array.

Idea:

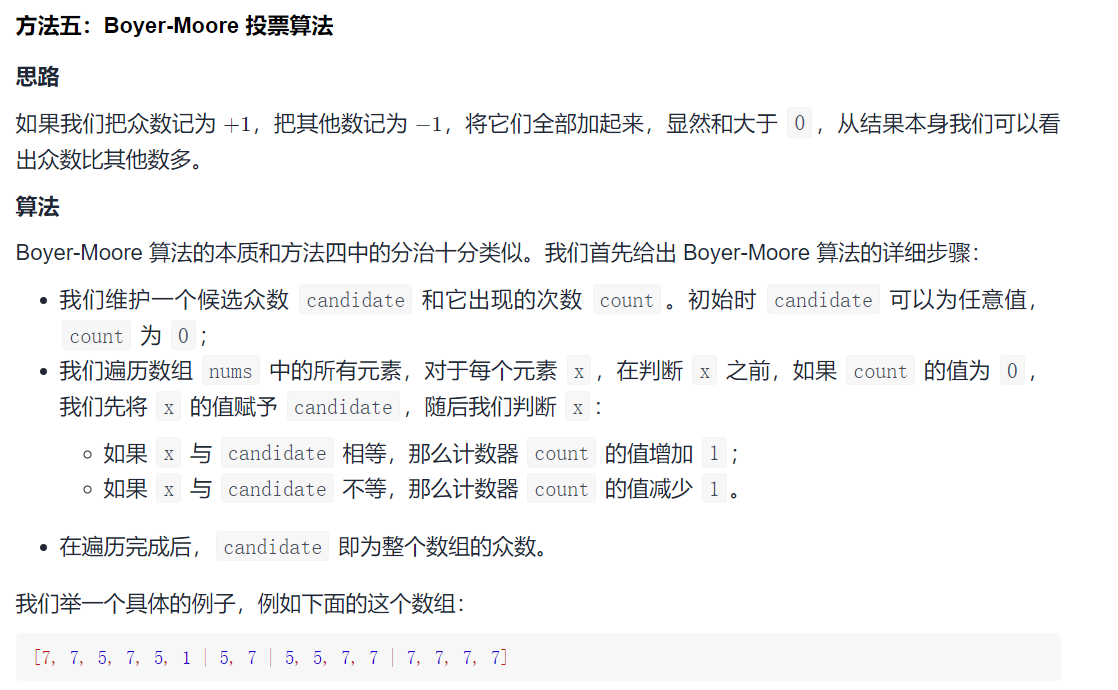
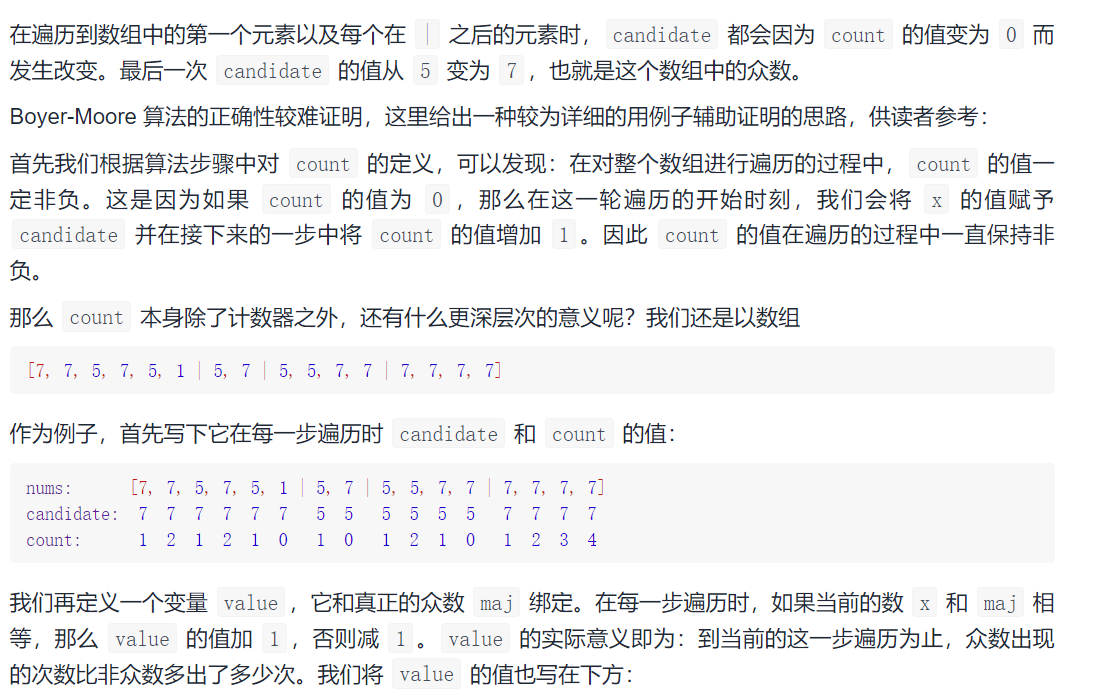
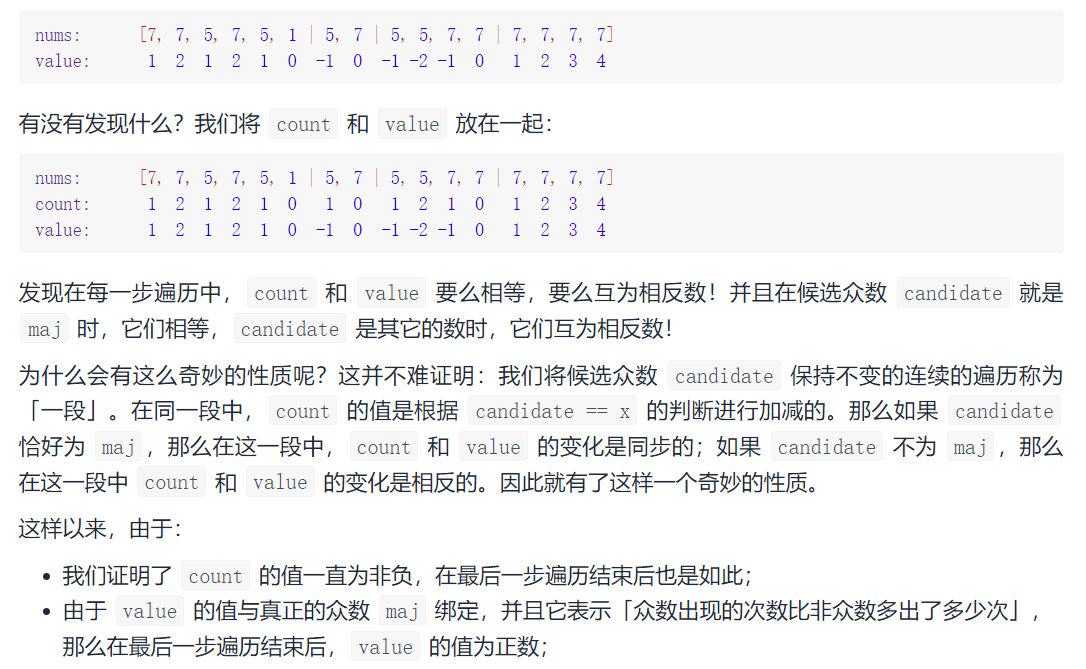
code:

    //Time complex O(N) space complex O(1)
    int majorityElement(vector<int>& nums){
        int thinkAns=nums[0],count=0;//thinkAns random assignment
        for(int x:nums){
            if(x==thinkAns)
                count++;
            else if(--count<0){
                thinkAns=x;
                count=1;
            }
        }
        return thinkAns;      
    }

    //Junk code here
    //Time complex O(N^2) space complex O(N)
    int majorityElement1(vector<int>& nums) {
        int n=nums.size();
        map<int,int> m;//< number, times >
        for(int x:nums){
            if(m.find(x)==m.end())
                m[x]=1;
            else
                m[x]++;
        }
        //The most frequently found
        int maxTime=0;
        int ans;
        for(pair<int,int> p:m){
            if(p.second>maxTime){
                maxTime=p.second;
                ans=p.first;
            }
        }
        return ans;
    }

2. Find all letter words in the string

Title Description:

Given two strings ， s ， and p, find the substrings of ， p ， of all ， p ， in ， s ， and return the starting indexes of these substrings. The order in which answers are output is not considered.

Ectopic words refer to strings formed by rearrangement of the same letters (including the same string).

Idea:

According to the requirements of the topic, we need to find the ectopic word of string pp in string ss. Because the length of the ectopic word of string pp must be the same as that of string pp, we can construct a sliding window with the same length as that of string pp in string ss, and maintain the number of each letter in the window; When the number of each letter in the window is the same as that in the string pp, it indicates that the current window is an ectopic word of the string pp.

Algorithm:

In the implementation of the algorithm, we can use an array to store the string pp and the number of each letter in the sliding window.

Details:

When the length of string ss is less than the length of string pp, there must be no ectopic word of string pp in string ss. However, since a window with the same length as the string pp cannot be constructed in the string ss, this situation needs to be handled separately.

Code implementation:

    vector<int> findAnagrams(string s, string p) {
        vector<int> ans;
        int n1=s.size(),n2=p.size();
        if(n1<n2)
            return ans;
        vector<int> sCount(26),pCount(26);
        for(int i=0;i<n2;i++){
            sCount[s[i]-'a']++;
            pCount[p[i]-'a']++;
        }
        if(sCount==pCount)
            ans.emplace_back(0);
        for(int i=0;i<n1-n2;i++){
            --sCount[s[i]-'a'];
            ++sCount[s[i+n2]-'a'];
            if(sCount==pCount)
                ans.emplace_back(i+1);
        }
        return ans;
    }

3. The number of consecutive subarrays whose product is less than K

Title Description:

Give an array of positive integers ， nums and the integer ， k.

Please find out the number of consecutive subarrays in the array whose product is less than k +.

 

Method 1 (binary search):

Code implementation:

//In order not to exceed the range in the calculation process, log (x * y) = logx + log is taken, so prefix is used to store prefix and
int numSubarrayProductLessThanK(vector<int>& nums, int k) {
    if (k == 0)
        return 0;
    int n = nums.size();
    vector<double> prefix(n+1);//prefix[i] indicates the prefix and of [0, i-1]
    prefix[0] = 0;
    for (int i = 1; i <= n; i++) {
        prefix[i] = prefix[i - 1] + log(nums[i - 1]);//Prefix [i] - prefix [J] represents the sum of [j,i-1]
    }
    double logk = log(k);
    int ans = 0;
    int N = prefix.size();
    int low = 0, high = N - 1,mid=low+((high-low)>>1);
    for (int i = 0; i < N; i++) {
        //Dichotomy
        low = i + 1; high = N;
        while (low < high) {
            mid = low + ((high - low) >> 1);
            if (prefix[mid] < prefix[i] + logk - 1e-9)
                low = mid + 1;
            else
                high = mid;
        }
        ans += low-1 - i;
    }
    return ans;
}

Method 2: (double pointer)

Code implementation:

//Double pointer
int numSubarrayProductLessThanK(vector<int>& nums, int k) {
    if (k <=1)
        return 0;
    int n = nums.size();
    int prod = 1, ans = 0, left = 0;
    for (int right = 0; right < n; right++) {
        prod *= nums[right];
        while (prod >= k)
            prod /= nums[left++];
        ans += right - left + 1;
    }
    return ans;
}

4. Maximum subarray and

Title Description:

Give you an integer array {nums. Please find a continuous sub array with the maximum sum (the sub array contains at least one element) and return its maximum sum.

A subarray is a contiguous part of an array.

 
Algorithm and idea:

Code implementation:

    //dynamic programming
    int maxSubArray(vector<int>& nums) {
        int pre = 0, maxAns = nums[0];
        for (int x : nums) {
            pre = max(pre + x, x);//Small with updates
            maxAns = max(maxAns, pre);//Record the maximum at the same time
        }
        return maxAns;
    }

5. Subarray with and K

Title Description:

Give you an integer array ， nums ， and an integer ， k. please count and return the number of consecutive sub arrays in the array and ， k ，.  

 

Idea: prefix and + hash optimization

Code:

    //Time complex O(n) space complex O(n)
    int subarraySum(vector<int>& nums, int k){
        int count=0,pre=0;
        unordered_map<int,int> mp;
        mp[0]=1;
        for(int x:nums){
            pre+=x;
            if(mp.find(pre-k)!=mp.end())
                count+=mp[pre-k];
            mp[pre]++;
        }
        return count;
    }