reference resources:
https://blog.csdn.net/duuuhs/article/details/89167231
https://blog.csdn.net/realYuzhou/article/details/109299625
summary
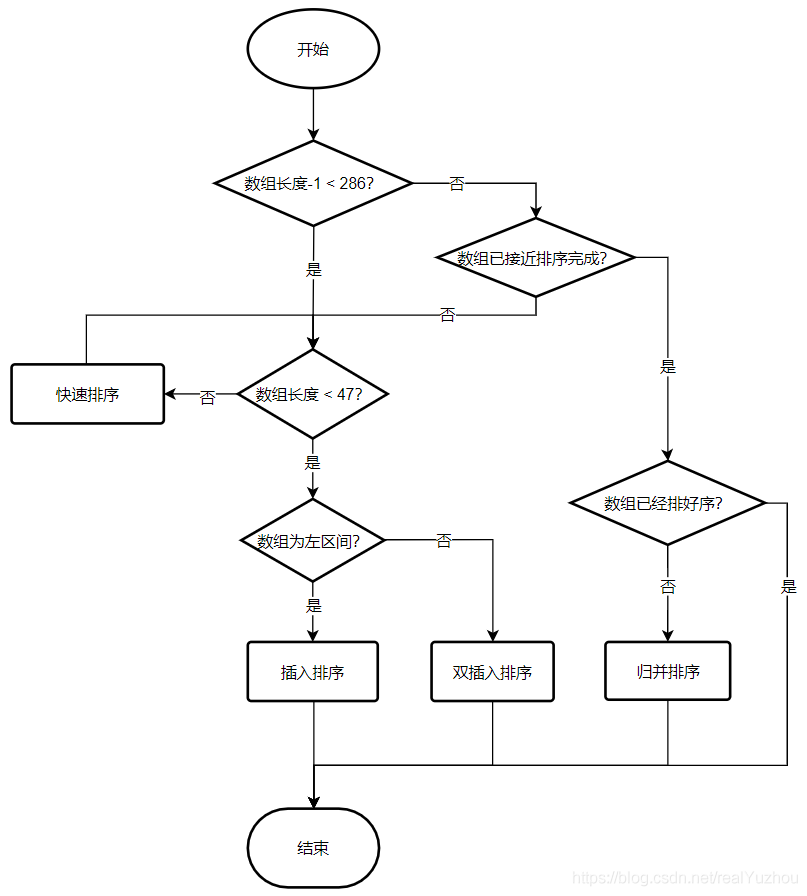
Collections. The bottom layer of the sort () method also calls arrays For the sort () method, let's explore its source code through the test case debug. First, let's talk about the results. We use insertion sorting, biaxial fast sorting and merge sorting
Dual pivot quicksort: as the name suggests, there are two axis elements pivot 1, pivot 2, and pivot ≤
Pivot 2, divide the sequence into three segments: x < pivot 1, pivot 1 ≤ x ≤ pivot 2, x > pivot 2, and then recurse the three segments respectively. This algorithm is usually more efficient than the traditional fast scheduling algorithm, so it is called arrays A concrete implementation of sorting basic types of data in Java.
General process:
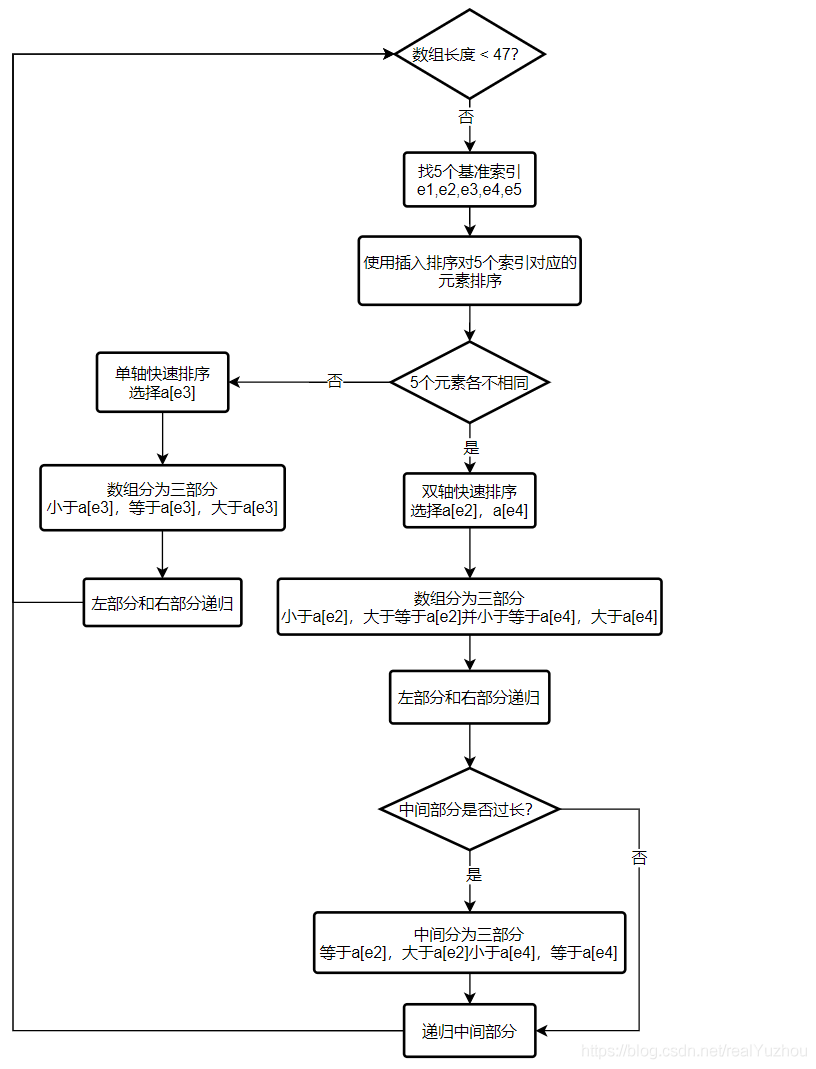
Quick sort section expansion
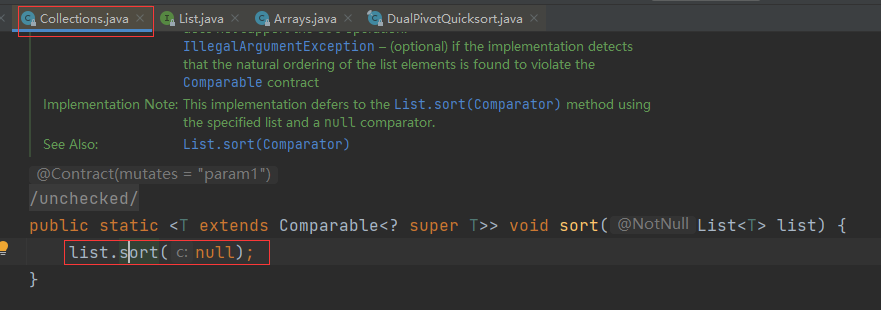
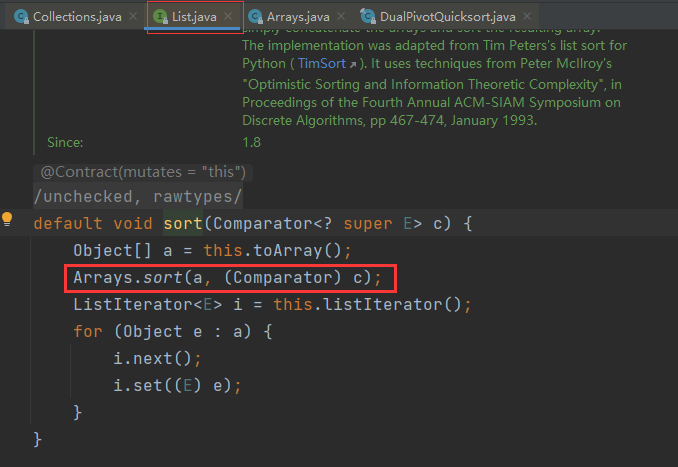
case
public static void main(String[] args) {
int[] nums = new int[]{6,5,4,3,2,1};
List<Integer> list = Arrays.asList(6, 5, 4, 3, 2, 1);
Arrays.sort(nums);
Collections.sort(list);
System.out.println(Arrays.toString(nums));
System.out.println(list);
}
Operation results
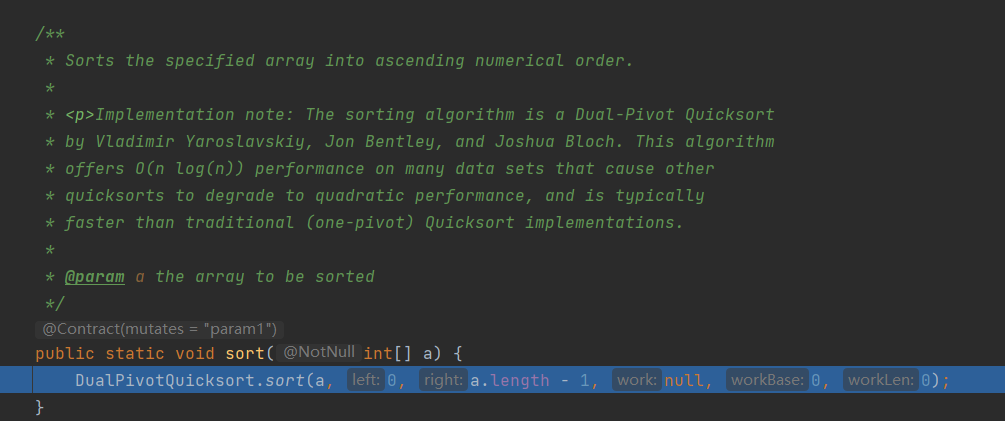
1. Enter arrays Sort() method
/**
* Sorts the specified array into ascending numerical order.
*
* <p>Implementation note: The sorting algorithm is a Dual-Pivot Quicksort
* by Vladimir Yaroslavskiy, Jon Bentley, and Joshua Bloch. This algorithm
* offers O(n log(n)) performance on many data sets that cause other
* quicksorts to degrade to quadratic performance, and is typically
* faster than traditional (one-pivot) Quicksort implementations.
*
* @param a the array to be sorted
*/
public static void sort(int[] a) {
DualPivotQuicksort.sort(a, 0, a.length - 1, null, 0, 0);
}
Comments on Methods

2 enter the static method sort inside the DualPivotQuicksort class
Comments on Methods

3. Follow the sort process


1. Use quick sort for arrays with sorting range less than 286
// Use Quicksort on small arrays
if (right - left < QUICKSORT_THRESHOLD) {
sort(a, left, right, true);
return;
}
// Merge sort
......
2. Enter the sort method to judge whether the array length is less than 47. If it is less than 47, insert sorting is directly adopted. Otherwise, execute 3.


// Use insertion sort on tiny arrays
if (length < INSERTION_SORT_THRESHOLD) {
// Insertion sort
......
}
3. Use the formula length/8+length/64+1 to approximately calculate 1 / 7 of the array length.
// Inexpensive approximation of length / 7
int seventh = (length >> 3) + (length >> 6) + 1;
4. Take 5 equidistant points based on experience.

/*
* Sort five evenly spaced elements around (and including) the
* center element in the range. These elements will be used for
* pivot selection as described below. The choice for spacing
* these elements was empirically determined to work well on
* a wide variety of inputs.
*/
int e3 = (left + right) >>> 1; // The midpoint
int e2 = e3 - seventh;
int e1 = e2 - seventh;
int e4 = e3 + seventh;
int e5 = e4 + seventh;
5. Insert and sort these five elements
// Sort these elements using insertion sort
if (a[e2] < a[e1]) { long t = a[e2]; a[e2] = a[e1]; a[e1] = t; }
if (a[e3] < a[e2]) { long t = a[e3]; a[e3] = a[e2]; a[e2] = t;
if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; }
}
if (a[e4] < a[e3]) { long t = a[e4]; a[e4] = a[e3]; a[e3] = t;
if (t < a[e2]) { a[e3] = a[e2]; a[e2] = t;
if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; }
}
}
if (a[e5] < a[e4]) { long t = a[e5]; a[e5] = a[e4]; a[e4] = t;
if (t < a[e3]) { a[e4] = a[e3]; a[e3] = t;
if (t < a[e2]) { a[e3] = a[e2]; a[e2] = t;
if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; }
}
}
}
6. Select a[e2] and a[e4] as pivot 1 and pivot 2 respectively. Since step 5 is sorted, there must be pivot 1 < = pivot 2. Define two pointers, less and great. Less starts from the leftmost and traverses to the right until the first element not less than pivot1 is found. Great starts from the right and traverses to the left until the first element not greater than pivot2 is found.
/*
* Use the second and fourth of the five sorted elements as pivots.
* These values are inexpensive approximations of the first and
* second terciles of the array. Note that pivot1 <= pivot2.
*/
int pivot1 = a[e2];
int pivot2 = a[e4];
/*
* The first and the last elements to be sorted are moved to the
* locations formerly occupied by the pivots. When partitioning
* is complete, the pivots are swapped back into their final
* positions, and excluded from subsequent sorting.
*/
a[e2] = a[left];
a[e4] = a[right];
/*
* Skip elements, which are less or greater than pivot values.
*/
while (a[++less] < pivot1);
while (a[--great] > pivot2);
7. Next, define the pointer k to traverse to the right from less-1 to great, move the elements less than pivot1 to the left of less, and move the elements greater than pivot2 to the right of great. Note here that we know that the element at great is smaller than pivot 2, but it depends on the size relationship of pivot 1. If it is smaller than pivot 1, it needs to be moved to the left of less, otherwise it only needs to be exchanged to k.
/*
* Partitioning:
*
* left part center part right part
* +--------------------------------------------------------------+
* | < pivot1 | pivot1 <= && <= pivot2 | ? | > pivot2 |
* +--------------------------------------------------------------+
* ^ ^ ^
* | | |
* less k great
*
* Invariants:
*
* all in (left, less) < pivot1
* pivot1 <= all in [less, k) <= pivot2
* all in (great, right) > pivot2
*
* Pointer k is the first index of ?-part.
*/
outer:
for (int k = less - 1; ++k <= great; ) {
short ak = a[k];
if (ak < pivot1) { // Move a[k] to left part
a[k] = a[less];
/*
* Here and below we use "a[i] = b; i++;" instead
* of "a[i++] = b;" due to performance issue.
*/
a[less] = ak;
++less;
} else if (ak > pivot2) { // Move a[k] to right part
while (a[great] > pivot2) {
if (great-- == k) {
break outer;
}
}
if (a[great] < pivot1) { // a[great] <= pivot2
a[k] = a[less];
a[less] = a[great];
++less;
} else { // pivot1 <= a[great] <= pivot2
a[k] = a[great];
}
/*
* Here and below we use "a[i] = b; i--;" instead
* of "a[i--] = b;" due to performance issue.
*/
a[great] = ak;
--great;
}
}
8. Exchange the pivots to their final position
// Swap pivots into their final positions
a[left] = a[less - 1]; a[less - 1] = pivot1;
a[right] = a[great + 1]; a[great + 1] = pivot2;
9. Recursively sort the left and right parts, excluding known pivots
// Sort left and right parts recursively, excluding known pivots
sort(a, left, less - 2, leftmost);
sort(a, great + 2, right, false);
10. For the middle part, if the array length is greater than 4 / 7, recurse the middle part
/*
* If center part is too large (comprises > 4/7 of the array),
* swap internal pivot values to ends.
*/
if (less < e1 && e5 < great) {
/*
* Skip elements, which are equal to pivot values.
*/
while (a[less] == pivot1) {
++less;
}
while (a[great] == pivot2) {
--great;
}
/*
* Partitioning:
*
* left part center part right part
* +----------------------------------------------------------+
* | == pivot1 | pivot1 < && < pivot2 | ? | == pivot2 |
* +----------------------------------------------------------+
* ^ ^ ^
* | | |
* less k great
*
* Invariants:
*
* all in (*, less) == pivot1
* pivot1 < all in [less, k) < pivot2
* all in (great, *) == pivot2
*
* Pointer k is the first index of ?-part.
*/
outer:
for (int k = less - 1; ++k <= great; ) {
short ak = a[k];
if (ak == pivot1) { // Move a[k] to left part
a[k] = a[less];
a[less] = ak;
++less;
} else if (ak == pivot2) { // Move a[k] to right part
while (a[great] == pivot2) {
if (great-- == k) {
break outer;
}
}
if (a[great] == pivot1) { // a[great] < pivot2
a[k] = a[less];
/*
* Even though a[great] equals to pivot1, the
* assignment a[less] = pivot1 may be incorrect,
* if a[great] and pivot1 are floating-point zeros
* of different signs. Therefore in float and
* double sorting methods we have to use more
* accurate assignment a[less] = a[great].
*/
a[less] = pivot1;
++less;
} else { // pivot1 < a[great] < pivot2
a[k] = a[great];
}
a[great] = ak;
--great;
}
}
}
// Sort center part recursively
sort(a, less, great, false);
4. Summary
Arrays.sort has greatly improved the sorting efficiency of ascending array, descending array and repeating array. There are several major optimizations.
- For small arrays, insert sorting is more efficient. When recursion is less than 47, insert sorting is used instead of fast sorting, which significantly improves the performance.
- Two pivot s are used in the double axis fast platoon. Each round divides the array into three segments, which skillfully reduces the number of recursion without significantly increasing the number of comparisons.
- The choice of pivot adds randomness, but it does not bring the overhead of random numbers.
- The duplicate data is optimized to avoid unnecessary exchange and recursion.