D - Kth Excluded

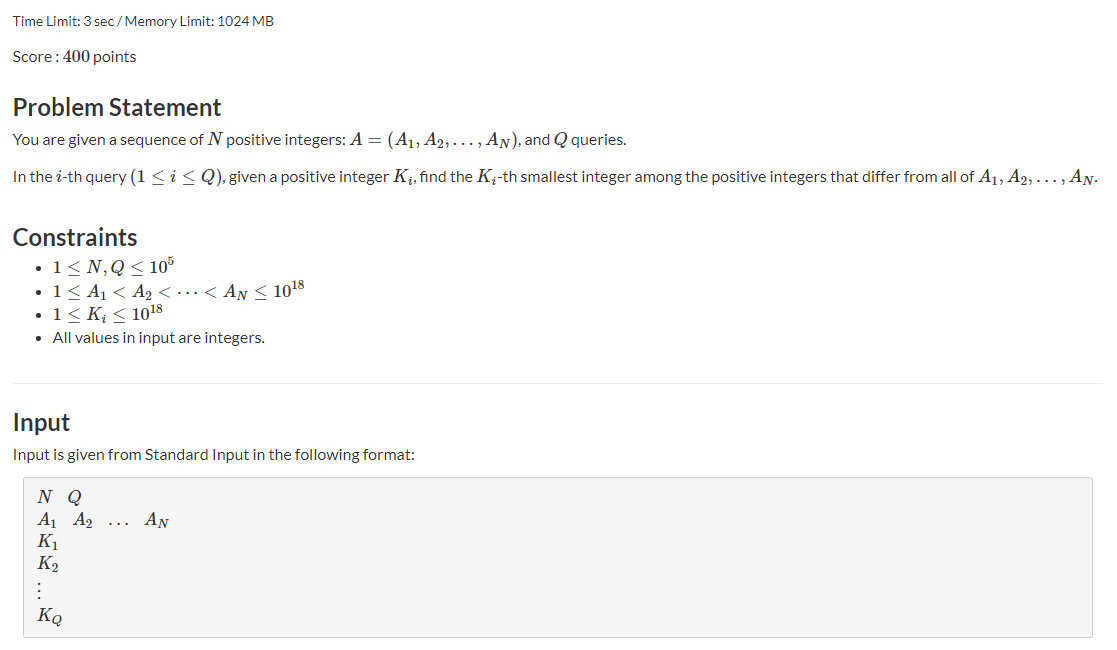
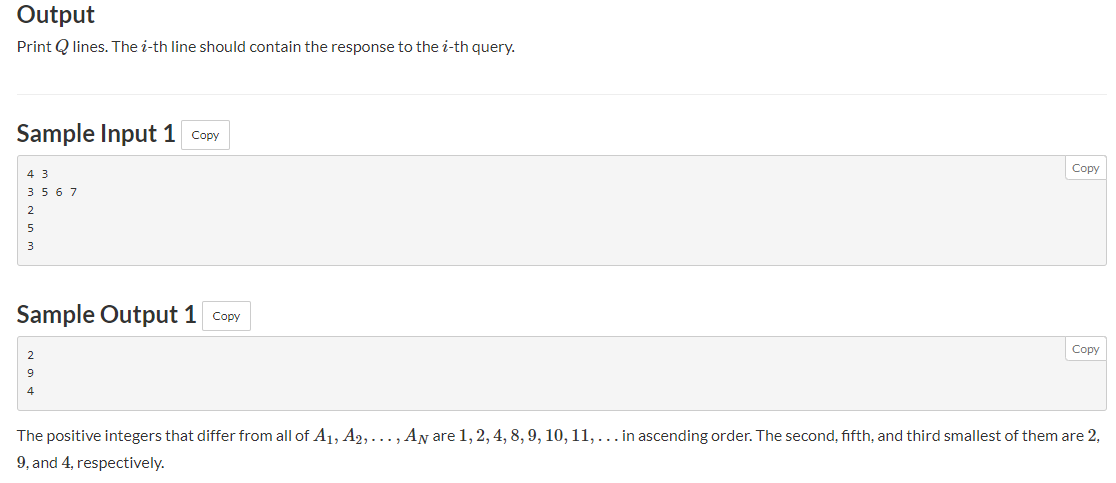
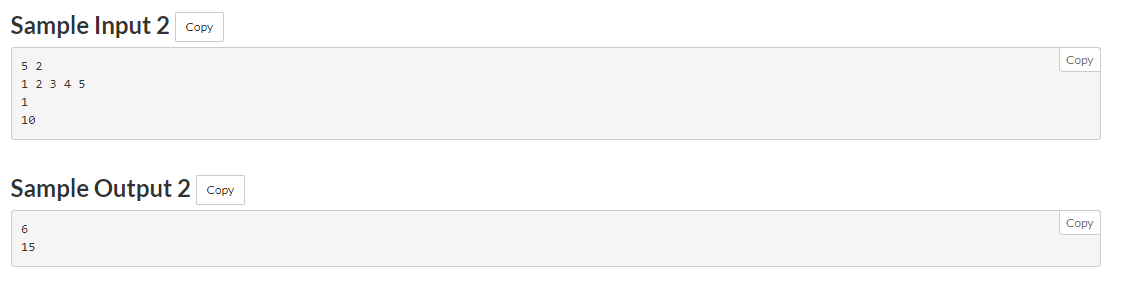
Question meaning: give n numbers, ask q times, and ask the k-th largest number each time (after removing the N numbers on the number axis, the k-th largest number)
Idea: for these n numbers, process out how many numbers in front of the current number have not been removed (how many numbers are on the number axis), and then when you ask the k-th number, find the number in that range. After finding the position, count k bits to the right from the current position, which is the number to be found.
For example, in example 3, 5, 6, 7, each number is saved, and the first few numbers are not removed, that is, 2, 3, 3
When looking for the third place, it is obvious that a[2]=3, which is in line with the meaning of the question. There are three numbers in front of it. Then this number is the number that subtracts the number existing in front, and then count one from the number of 3, that is, 4, which is the answer.
Because if you want to know the k-th number, you must first find the interval that matches the answer, and find it according to the number in front of each number. After finding the interval, you need to know how many numbers are in front of the previous number. After removing them, the corresponding number from the previous number to the next number is the answer.

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+10;
int n,q;
ll a[N],k;
int main() {
    scanf("%d%d",&n,&q);
    for(int i=1;i<=n;i++) {
        ll x;
        scanf("%lld",&x);
        a[i]=x-i;   
    }
    a[n+1]=1e18+10;
    while(q--) {
        scanf("%lld",&k);
        int l=0,r=n+1;
        while(l<r) {
            int mid=l+r>>1;
            if(k>a[mid]) l=mid+1;
            else r=mid;
        }
        printf("%lld\n",k+l-1);
        //k-=a[l-1]
        //k+l+a[k-1]
    }
    return 0;
}

E - White and Black Balls

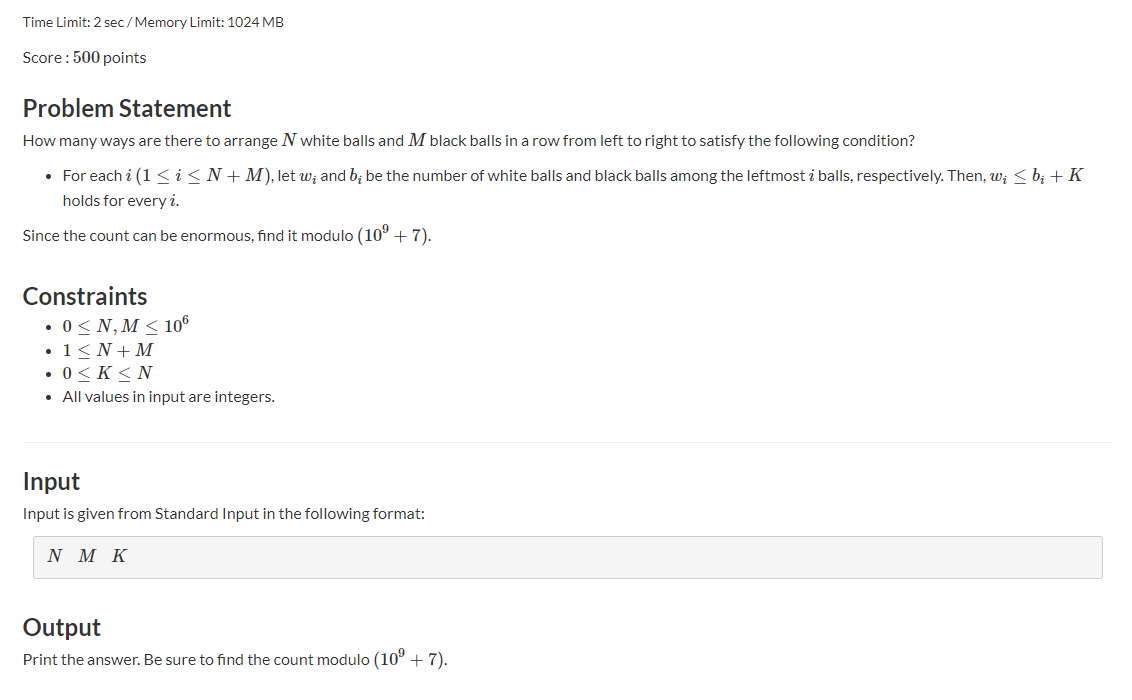
Meaning: give N white balls and M black balls, arranged from left to right, but Wi is the number of white balls from left to right to position i. Bi is the number of black balls, which should be met when arranging W i − B i < = K Wi-Bi<=K Wi − Bi < = k, how many permutations are there.
Idea: on the coordinate axis, take the number of white balls as one grid to the right and the number of black balls as one grid to the up. Finally, there are n white balls and m black balls, and the end point is ( n , m ) (n,m) (n,m), solve from ( 0 , 0 ) (0,0) (0,0) to ( n , m ) (n,m) The number of legal paths of (n,m), which represents W i − B i < = K Wi-Bi<=K Wi − Bi < = k, the solution method is the same as that of calculating Cartland number.

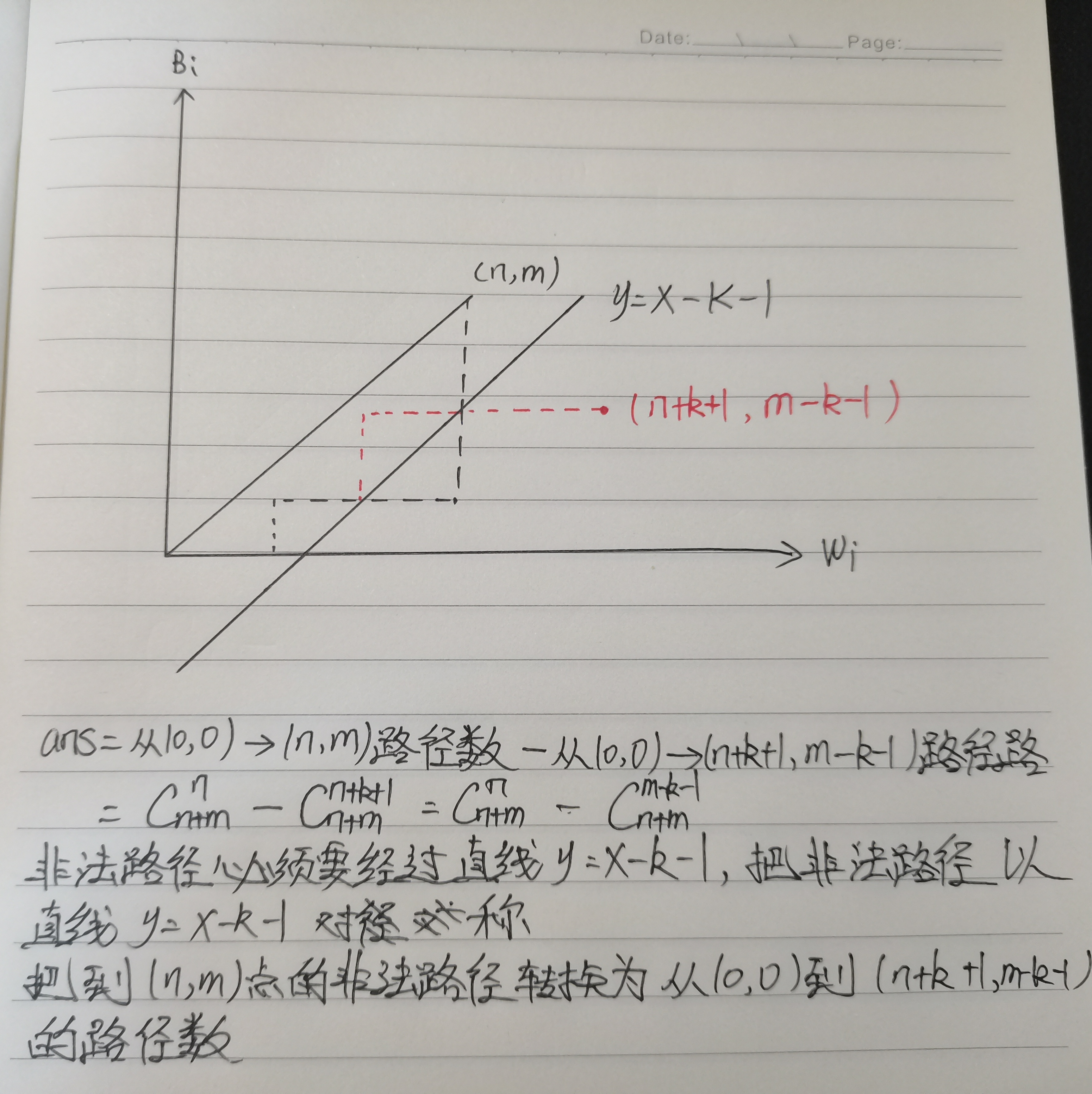
Personally, I think this question is helpful for the understanding of Cartland number. It can be regarded as a small note.

Finally, it should be noted that for the subtraction and remainder of two combinatorial numbers, one should be added first m o d mod mod, take the remainder m o d mod mod, because after the remainder, the latter number is not necessarily smaller than the previous one.

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 2e6 + 7;
const int mod = 1e9 + 7;
int fact[N], infact[N];
int qmi(int q, int k, int p) {
    int res = 1;
    while (k) {
        if (k & 1) res = (ll)res * q % p;
        q = (ll)q * q % p;
        k >>= 1;
    }
    return res;
}
void init() {
    fact[0] = infact[0] = 1;
    for (int i = 1; i < N; i++) {
        fact[i] = (ll)fact[i - 1] * i % mod;
        infact[i] = (ll)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
    }
}

int main() {
    int n, m, k;
    scanf("%d%d%d", &n, &m, &k);
    if (n > k + m) {
        cout << 0 << endl;
        return 0;
    }
    init();
    ll a = 0, b = 0;
    a = (ll)fact[n + m] * infact[n] % mod * infact[m] % mod;
    b = (ll)fact[n + m] * infact[n - k - 1] % mod * infact[m + k + 1] % mod;
    printf("%lld\n", (a - b + mod) % mod);
    return 0;
}

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
int qmi(int q, int k) {
    int res = 1;
    while (k) {
        if (k & 1) res = (ll)res * q % mod;
        q = (ll)q * q % mod;
        k >>= 1;
    }
    return res;
}
ll get(ll a, ll b) {
    ll res = 1;
    for (int i = a; i > a - b; i--) res = (ll)res * i % mod;
    for (int i = b; i; i--) res = (ll)res * qmi(i, mod - 2) % mod;
    return res;
}
int main() {
    ll n, m, k;
    cin >> n >> m >> k;
    if (m + k < n) {
        cout << 0 << endl;
        return 0;
    }
    ll res1 = get(n + m, n);
    ll res2 = get(n + m, m + k + 1);
    ll res = (res1 - res2 + mod) % mod;
    cout << res << endl;
}

To be continued
If you have any suggestions or criticisms and additions, please leave a message and point it out. Thank you very much