recently, I was reviewing the data structure. In order to deepen my understanding of B-tree, I sorted out the following notes, and then implemented B-tree in C language; I haven't used C language for a long time. Some parts of the code don't conform to the specification or there are problems in understanding this article. Please correct me;
1, B-tree definition
B tree, also known as multi-path balanced search tree, the maximum number of children of all nodes in B tree is the order of B tree. The definition of m-order B-tree is as follows: empty tree or M-ary tree satisfying the following characteristics:
1) each node in the tree has at most m subtrees, that is, at most m-1 keywords;
2) if the root node is not a terminal node, there are at least two subtrees, that is, at least one keyword;
3) all non leaf nodes except the root node have at least
⌈
m
/
2
⌉
\lceil m/2 \rceil
⌈ m/2 ⌉ subtree, i.e. at least
⌈
m
/
2
⌉
\lceil m/2 \rceil
⌈ m/2 ⌉ - 1 keyword;
4) all non leaf node structures are as follows:
Where, Ki (i=0, 1, 2,..., n) is the keyword of the node and meets K1 < K2 <... < kn; Pi is the pointer to the root node of the subtree, and the pointer P All node keywords in the subtree referred to in i-1 are less than K i，P All node keywords in the subtree referred to by i are greater than K i. Among them ⌈ m / 2 ⌉ \lceil m/2 \rceil ⌈m/2⌉ - 1 ⩽ \leqslant ⩽ n ⩽ \leqslant ⩽ m - 1, indicating the number of keywords;
5) all empty nodes appear at the same level, and these empty nodes can be regarded as search failure;
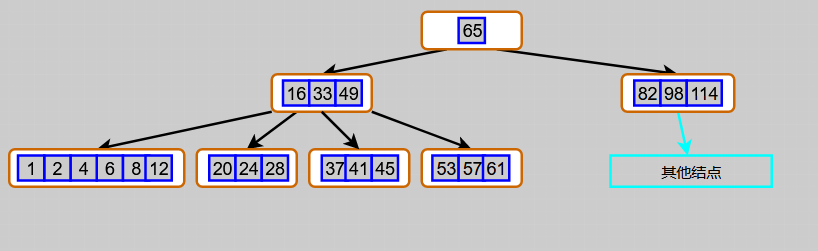Fig. 2 7th order B-tree
2, Properties of B-tree:
The properties discussed here do not count external nodes as leaf nodes;
1) the number of children of non leaf nodes is equal to the number of keywords plus 1;
2) the keyword in the node is incremented from left to right, and there are pointers to the subtree on both sides of the keyword;
3) height of B tree: for B tree with n keywords, height h and order m
i)h
⩾
\geqslant
⩾logm(n+1)
B tree has at most m sub trees and m-1 keywords at each node, so it should meet n
⩽
\leqslant
⩽ (m-1)
(
1
+
m
+
m
2
+
m
3
+
.
.
.
+
m
h
−
1
)
=
m
h
−
1
;
(1+m+m^2+m^3+...+m^{h-1})=m^h-1;
(1+m+m2+m3+...+mh−1)=mh−1;
ii)h
⩽
\leqslant
⩽log
⌈
m
/
2
⌉
\lceil m/2 \rceil
⌈m/2⌉((n+1)/2)+1;
if the number of keywords in each node is minimized, the height of B tree is maximum; At this time, the root node has a keyword and two subtrees, and all remaining nodes have
⌈
m
/
2
⌉
\lceil m/2 \rceil
⌈ m/2 ⌉ - 1 keyword, then the total number of keywords is 1 + 2 * (1+
⌈
m
/
2
⌉
\lceil m/2 \rceil
⌈m/2⌉+
⌈
m
/
2
⌉
\lceil m/2 \rceil
⌈m/2⌉^2+
⌈
m
/
2
⌉
\lceil m/2 \rceil
⌈m/2⌉^3+...+
⌈
m
/
2
⌉
h
−
2
)
∗
(
⌈
m
/
2
⌉
−
1
)
=
1
+
2
∗
(
⌈
m
/
2
⌉
h
−
1
−
1
\lceil m/2 \rceil^{h-2})*(\lceil m/2 \rceil-1)=1+2*(\lceil m/2 \rceil^{h-1} - 1
⌈m/2⌉h−2)∗(⌈m/2⌉−1)=1+2∗(⌈m/2⌉h−1−1) = 2*
⌈
m
/
2
⌉
h
−
1
\lceil m/2\rceil^{h-1}
⌈ m/2 ⌉ h − 1 - 1, so, n
⩾
\geqslant
⩾ 2*
⌈
m
/
2
⌉
h
−
1
\lceil m/2\rceil^{h-1}
⌈m/2⌉h−1 - 1;
3, Search of B-tree
similar to binary tree search, search the multi keyword ordered table from the root node every time, and make multi branch decisions according to the search results of the node;
B tree search steps are as follows:
1) the working pointer P points to the root node;
2) compare the keyword key with the keyword list of node P. if Ki=key, directly return the node and location i of this node; otherwise, until Ki is found
<
\lt
< key
<
\lt
< ki + 1, let P = P - > pi;
3) repeat the above steps until it is found or P is NULL; if P=NULL, it means it is not found;
4, Insertion of B-tree
The insertion of B tree is much more complex than binary search tree. The insertion of B tree may cause too many keywords in a node, which does not meet the definition of m-order B tree. At this time, the operation of node splitting will be involved. The process of inserting keywords into B tree is as follows:
1) location: find the insertion position (leaf node) with the search algorithm of B tree;
2) in the B tree, the number of keywords of each node is in the interval[
⌈
m
/
2
⌉
\lceil m/2 \rceil
⌈ m/2 ⌉ - 1, m-1], if the number of node keywords
⩽
\leqslant
⩽ m-2, after inserting the keyword, it still conforms to the definition of B tree and can be inserted directly; otherwise, the following node splitting operations should be performed:
from the middle position(
⌈
m
/
2
⌉
\lceil m/2 \rceil
⌈ m/2 ⌉) split the node after inserting the keyword, and select the location
⌈
m
/
2
⌉
\lceil m/2 \rceil
Carry the keyword at ⌈ m/2 ⌉ to the parent node, [0-
⌈
m
/
2
⌉
\lceil m/2 \rceil
The keyword at ⌈ m/2 ⌉ - 1] remains in the original node, and a new node is generated for storage[
⌈
m
/
2
⌉
\lceil m/2 \rceil
Keywords at ⌈ m/2 ⌉ + 1, m-1]; if the parent node does not meet the definition after carry, continue to carry up until the root node; if the root node does not meet the definition due to carry to the root node, recreate a root node, containing only carry keywords;
The following are the operation steps for inserting keywords in two cases:
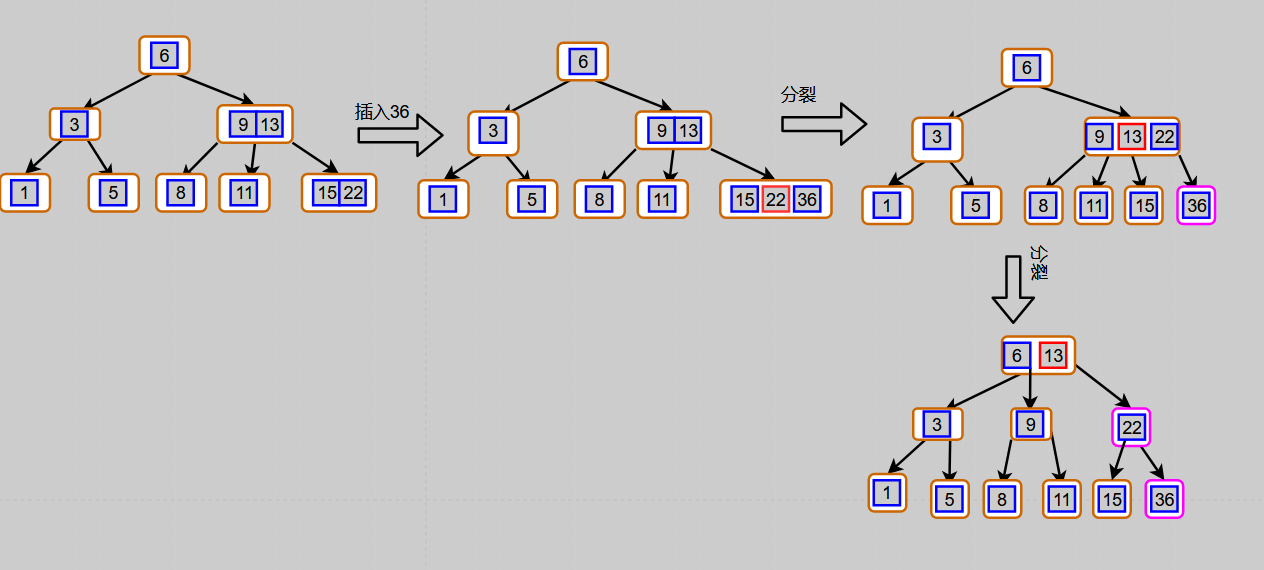
5, Deletion of B-tree
deleting a keyword may also lead to the node not conforming to the definition of B tree, which will involve the node merging operation. The process of deleting a keyword key from B tree is as follows (set the node where the deleted keyword is located as iNode, the sibling node as lNode, the right sibling node as rNode, and the parent node as pNode):
case 1) when iNode is not a leaf node: replace k with the predecessor or successor key 'of the key, and then delete the key'. At this time, the key 'must fall on the leaf node, so it is converted to case 2;
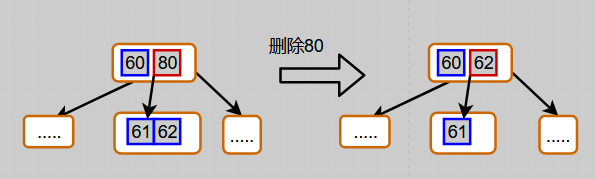
case 2) iNode is a leaf node, which can be divided into three cases:
① number of iNode keywords ⩾ ⌈ m / 2 ⌉ \geqslant \lceil m/2\rceil ⩾⌈ m/2 ⌉ indicates that after deleting the key, it still meets the B-tree definition and can be deleted directly;
② brothers can borrow enough. If the number of iNode keywords < ⌈ m / 2 ⌉ \lt \lceil m/2\rceil < ⌈ m/2 ⌉ and the number of lNode or rNode keywords ⩾ ⌈ m / 2 ⌉ \geqslant \lceil m/2\rceil ⩾⌈ m/2 ⌉, borrow from lNode (assuming that lNode can borrow enough); The borrowing process is as follows:
pointer p of pNode If i points to iNode, use K i instead of key, and then use the last keyword of lNode to supplement K of pNode i. If the last child node of lNode is not empty, insert this child node into iNode;
③ brothers are not enough. If the number of iNode, lNode and rNode keywords are all equal < ⌈ m / 2 ⌉ \lt \lceil m/2\rceil < ⌈ m/2 ⌉, the iNode and lNode or rNode after keyword deletion will be merged; when merging, the number of parent node keywords will be - 1. If this causes the parent node pNode to fail to meet the definition of number B (when pNode is the root node, the number of keywords of pNode) > \gt >1), then pNode should adjust (borrow or merge) with its left and right sibling nodes, and repeat the above steps until it meets the requirements of B-tree; The consolidation process is as follows:
i) if pNode is the root node and the number of keywords is 1, the keywords and child nodes of pNode plus the remaining information of iNode are incorporated into rNode (assuming that rNode exists), and rNode is the root node of B tree;
ii) if pNode is not the root and the pointer pi of pNode points to iNode, then the keyword K of pNode The remaining information of i and iNode is incorporated into rNode, and then the iNode is deleted;
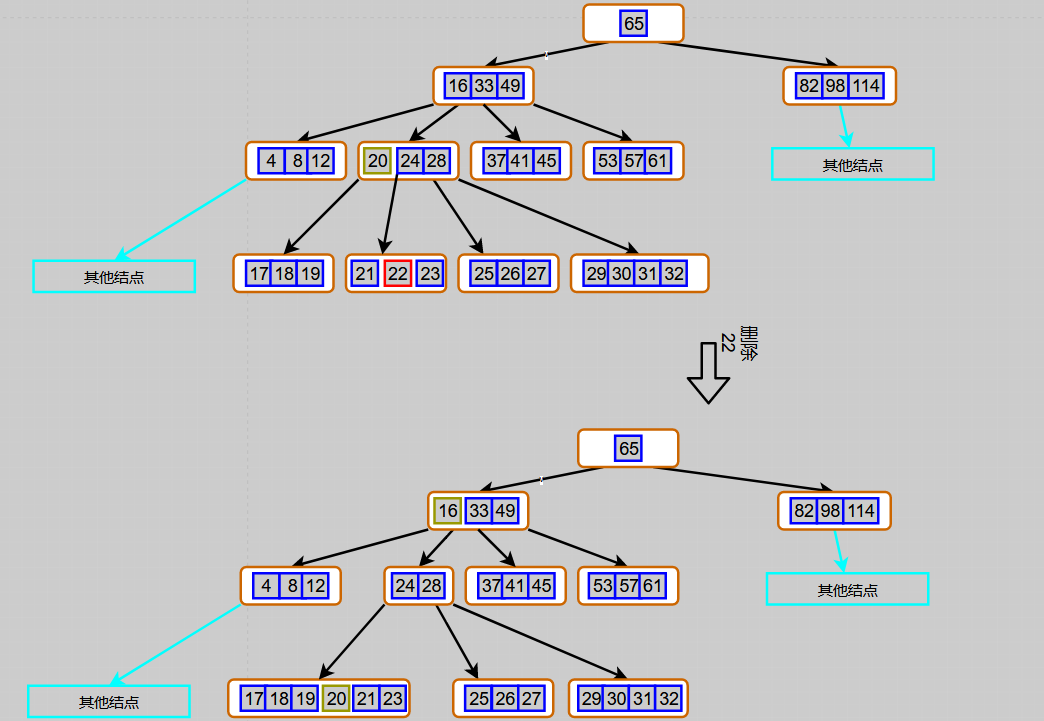
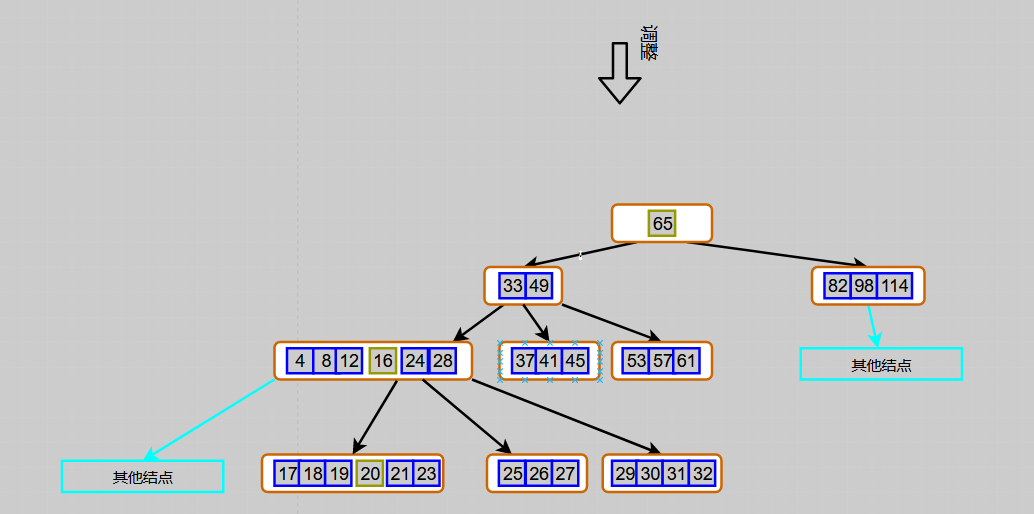
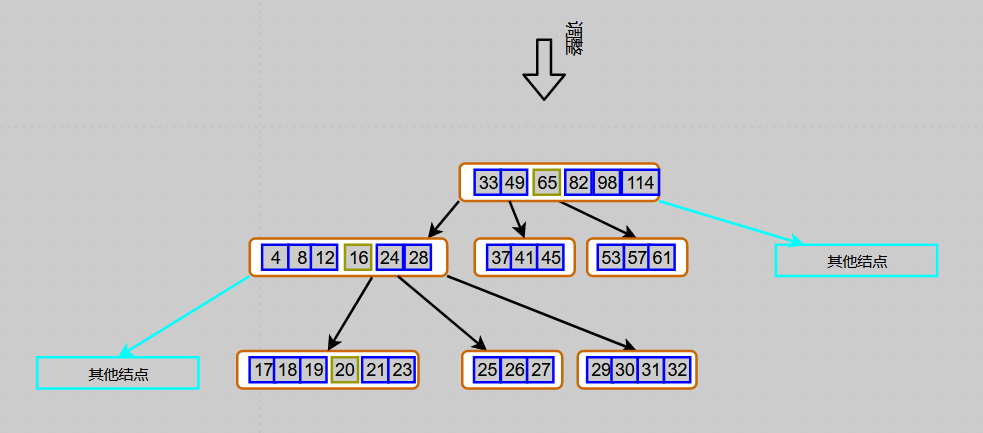Figure 6 7-order B-tree deletion keyword 22
6, C language implementation
The project structure is as follows:
1,BTree.h:
#pragma once
#define MAX_ Order 6 / / maximum order of B tree
#define TREE_ Order 4 / / order B
#define MIN_KEY_NUM (TREE_ORDER - 1)/2 / / minimum number of non root keywords
#define MAX_KEY_NUM TREE_ORDER - 1 / / maximum number of keywords per node
#define ROOT_MIN_KEY_NUM 1 / / maximum number of keywords in the root node
#define CEIL(x) (x+1)/2 / / round up
// Because the data of each node of the B tree is stored from the subscript 0, - 1
#define ROOT_INDEX (TREE_ORDER - 1)/2 / / the data index that needs to be carried during node splitting
#define NOT_FOUND -1 / / no flag found
// Keyword type
typedef int KeyType;
// Node data type
typedef struct MyType {
KeyType key;
}DataType;
// Status of BTree operation
enum Status{
OK,
ERROR
};
// Find status flags
enum Tag{
SUCCESS, //Search succeeded
FAIL, // Search failed
INSERT, // Find insertion location
DELETE
};
// BlanceTree node
typedef struct BTreeNode{
int keyNum;
int childNum;
BTreeNode *parent;
BTreeNode *child[TREE_ORDER];
DataType data[MAX_KEY_NUM];
}BTNode, *BTree;
// BTree search results
typedef struct {
BTNode *node; // Found node
int pos; // Key position in node
Tag tag; // Found
}Result;
// Initialization tree
Status InitBTree(BTree &T);
/* Initialization tree
dataList: Initial data list
*/
Status InitBTree(BTree &T, DataType *dataList, int dataNum);
// Insert data into tree
Status InsertData(BTree &T, DataType data);
// Find data insertion location according to keywords
Result SearchInsertPos(BTree T, KeyType key);
/* Add data to a node
T: The tree to which this node belongs
inPos: Insert location information
data: Data to insert
subNewNode: A new node generated by the splitting of child nodes due to too much data
*/
Status DataJoinNode(BTree &T, Result inPos, DataType data, BTNode* &subNewNode);
// Find data by keyword
DataType SearchDataByKey(BTree T, KeyType key);
// Find the location of data according to keywords
Result SearchData(BTree T, KeyType key);
// Delete data according to data location
Status DeleteData(BTree &T, Result dPos);
/* Merge the parent node, current node (iNode) and its left and right siblings in tree T
T: tree
pNode: iNode Parent node
lNode: iNode Left sibling node of
iIndex: iNode Subscript in pNode
rNode: iNode Right sibling node of
*/
Status MergeNode(BTree &T, BTNode* pNode, BTNode* lNode, int iIndex, BTNode* rNode);
// Find the last node of the tree with rootNode as the root
BTNode* FindLastNode(BTNode* rootNode);
// Delete data by keyword
Status DeleteData(BTree &T, KeyType key);
// Output BTree keywords in ascending order
void PrintBTree(BTree T);
2,BTree.cpp
#include<iostream>
#include"BTree.h"
using namespace std;
Status InitNewNode(BTNode* &newNode) {
newNode = new BTNode;
newNode->keyNum = 0;
newNode->childNum = 0;
newNode->parent = NULL;
for (int i = 0; i < TREE_ORDER; i++) {
newNode->child[i] = NULL;
}
return OK;
}
Status InitBTree(BTree &T) {
if (TREE_ORDER > MAX_ORDER) {
cout << "B Tree order is too large" << endl;
return ERROR;
}
else {
T = new BTNode;
T->keyNum = 0;
T->childNum = 0;
T->parent = NULL;
for (int i = 0; i < TREE_ORDER; i++) {
T->child[i] = NULL;
}
return OK;
}
}
Status InitBTree(BTree &T, DataType *dataList, int dataNum) {
if (InitBTree(T) == OK) {
for (int i = 0; i < dataNum; i++)
if (InsertData(T, dataList[i]) == ERROR)
return ERROR;
return OK;
}
return ERROR;
}
Status InsertData(BTree &T, DataType data) {
Result inPos = SearchInsertPos(T, data.key);
BTNode* subNewNode = NULL;
return DataJoinNode(T, inPos, data, subNewNode);
}
Result SearchInsertPos(BTree T, KeyType key) {
BTNode *p = NULL, *q = T;
int i = 0;
while (q) {
for (i = 0; i < q->keyNum && q->data[i].key < key; i++);
p = q;
q = q->child[i];
}
return {p, i, INSERT};
}
Status DataJoinNode(BTree &T, Result inPos, DataType data, BTNode* &subNewNode) {
BTNode *iNode = inPos.node;
int i = 0,k = 0;
if (iNode->keyNum < MAX_KEY_NUM) {// Case 1: direct insertion
for (i = iNode->keyNum; i > inPos.pos; i--) {
iNode->data[i] = iNode->data[i - 1];
iNode->child[i + 1] = iNode->child[i];
}
iNode->data[i] = data;
iNode->keyNum += 1;
if (subNewNode) {
iNode->child[i + 1] = subNewNode;
subNewNode->parent = iNode;
iNode->childNum += 1;
}
}else { // Case 2: node splitting
// Temporary array to save the data of this node after inserting keywords
DataType temp[TREE_ORDER];
BTNode* tempNodes[TREE_ORDER + 1];
for (i = 0; i < inPos.pos; i++) {
temp[i] = iNode->data[i];
tempNodes[i] = iNode->child[i];
}
tempNodes[i] = iNode->child[i];
tempNodes[i + 1] = subNewNode;
temp[i] = data;
for (; i < iNode->keyNum; i++) {
temp[i + 1] = iNode->data[i];
tempNodes[i + 2] = iNode->child[i + 1];
}
/* Node splitting
iNode Save the information on the left, and newNode saves the information on the right
*/
iNode->childNum = 0;
for (i = 0; i < TREE_ORDER; i++) {
if (tempNodes[i] && i <= ROOT_INDEX) {
iNode->child[i] = tempNodes[i];
iNode->childNum++;
}
else {
iNode->child[i] = NULL;
}
}
iNode->keyNum = ROOT_INDEX;
// Create a new node
BTNode* newNode;
InitNewNode(newNode);
newNode->keyNum = MAX_KEY_NUM - ROOT_INDEX;
for (i = ROOT_INDEX + 1, k = 0; i <= TREE_ORDER; i++,k++) {
newNode->data[k] = temp[i];
if (tempNodes[i]) {
newNode->child[k] = tempNodes[i];
newNode->childNum += 1;
tempNodes[i]->parent = newNode;
}
}
BTNode *pNode = iNode->parent; //Parent node of current node
if (pNode) { // The parent node is not empty. You can continue to carry to the upper level
for (i = 0; i < pNode->keyNum && pNode->data[i].key < temp[ROOT_INDEX].key; i++);
Result pInPos = { pNode, i, INSERT };
DataJoinNode(T, pInPos, temp[ROOT_INDEX], newNode);
}else { // The parent node is empty, that is, the current node is the root, and the root node is regenerated
BTNode* rootNode;
InitNewNode(rootNode);
rootNode->childNum = 2;
rootNode->keyNum = 1;
rootNode->child[0] = iNode;
rootNode->child[1] = newNode;
rootNode->data[0] = temp[ROOT_INDEX];
newNode->parent = rootNode;
iNode->parent = rootNode;
T = rootNode;
}
}
return OK;
}
DataType SearchDataByKey(BTree T, KeyType key) {
BTNode* p = T;
int i;
while (p) {
for (i = 0; i < p->keyNum; i++) {
if (p->data[i].key == key)
return p->data[i];
else if (p->data[i].key > key)
break;
}
p = p->child[i];
}
return { {NOT_FOUND} };
}
Result SearchData(BTree T, KeyType key) {
BTNode* p = T;
int i;
while (p) {
for (i = 0; i < p->keyNum; i++) {
if (p->data[i].key == key)
return { p, i, SUCCESS };
else if (p->data[i].key > key)
break;
}
p = p->child[i];
}
return { NULL, -1, FAIL };
}
Status MergeNode(BTree &T, BTNode* pNode, BTNode* lNode, int iIndex, BTNode* rNode) {
if (!pNode || !T || iIndex < 0 || !rNode && !lNode)
return ERROR;
int i = 0;
BTNode* iNode = pNode->child[iIndex];
// Suppose pnode - > child [Iindex] points to iNode
if (rNode && rNode->keyNum > MIN_KEY_NUM) {
/* If the number of keywords after rNode borrowing is greater than the threshold
Borrow from rNode to iNode: suppose pnode - > child [i] points to iNode
*/
// (1) Add pnode - > data [Iindex] to iNode;
iNode->data[iNode->keyNum++] = pNode->data[iIndex];
// (2) Replace rnode - > data [0] with pnode - > data [Iindex]
pNode->data[iIndex] = rNode->data[0];
// (3) Merge rnode - > child [0] into iNode
if (rNode->child[0])
rNode->child[0]->parent = iNode;
iNode->child[iNode->childNum++] = rNode->child[0];
// (4) Delete data[0] and child[0] from rNode
for (i = 0; i < rNode->keyNum - 1; i++) {
rNode->data[i] = rNode->data[i + 1];
}
rNode->keyNum--;
if (rNode->childNum > 0) {
for (i = 0; i < rNode->childNum - 1; i++) {
rNode->child[i] = rNode->child[i + 1];
}
rNode->child[--rNode->childNum] = NULL;
}
}
else if (lNode && lNode->keyNum > MIN_KEY_NUM) {
/* If the number of keywords after lNode borrowing is greater than the threshold
Borrow from lNode to iNode:
*/
// (1) Add pnode - > data [Iindex - 1] to iNode;
for (i = iNode->keyNum; i > 0; i--)
iNode->data[i] = iNode->data[i - 1];
iNode->data[0] = pNode->data[iIndex - 1];
iNode->keyNum++;
// (2) Replace lnode - > data [End] with pnode - > data [Iindex - 1] and delete lnode - > data [End]
pNode->data[iIndex - 1] = lNode->data[--lNode->keyNum];
// (3) Merge lnode - > child [End] into iNode and delete it
if (iNode->childNum > 0) {
for (i = iNode->childNum; i > 0; i++)
iNode->child[i] = iNode->child[i - 1];
iNode->child[0] = lNode->child[--lNode->childNum];
iNode->child[0]->parent = iNode;
lNode->child[lNode->childNum] = NULL;
}
} else if (!pNode->parent && pNode->keyNum <= ROOT_MIN_KEY_NUM) { // pNode is the root node, and the number of keywords after borrowing is less than the threshold
if (rNode && rNode->keyNum == MIN_KEY_NUM) {
/*
1,If rNode exists, the remaining information of iNode and root node information are merged into rNode;
2,Make rNode the root node
*/
// Merge the root node and the remaining keywords of iNode into rNode
for (i = rNode->keyNum - 1; i >= 0; i++)
rNode->data[i + MIN_KEY_NUM] = rNode->data[i];
for (i = 0; i < iNode->keyNum; i++) {
rNode->data[i] = iNode->data[i];
rNode->keyNum++;
}
rNode->data[i] = pNode->data[0];
rNode->keyNum++;
// Move the remaining child nodes of iNode to rNode
for (i = rNode->childNum - 1; i >= 0; i++)
rNode->child[i + MIN_KEY_NUM] = rNode->child[i];
for (i = 0; i < iNode->childNum && iNode->child[i]; i++) {
iNode->child[i]->parent = rNode; // Modify parent pointer of iNode child node
rNode->child[i] = iNode->child[i];
rNode->childNum++;
}
delete iNode;
T = rNode;
}
else if (lNode && lNode->keyNum == MIN_KEY_NUM) {
/*
1,If the lNode exists, the remaining information of the iNode and the root node information are merged into the lNode;
2,Make lNode the root node
*/
// Merge the root node and the remaining keywords of iNode into lNode
lNode->data[lNode->keyNum++] = pNode->data[0];
for (i = 0; i < iNode->keyNum; i++)
lNode->data[lNode->keyNum++] = iNode->data[i];
// Merge the remaining child nodes of iNode into lNode
for (i = 0; i < iNode->childNum && iNode->child[i]; i++) {
iNode->child[i]->parent = lNode;
lNode->child[lNode->childNum++] = iNode->child[i];
}
delete iNode;
T = lNode;
}
} else {
if (lNode) {
/*
lNode Yes, borrow a bit from pNode plus the remaining information of iNode and merge it into lNode
*/
//(1) Pnode - > data [Iindex - 1] and the remaining keywords of iNode are incorporated into lNode
lNode->data[lNode->keyNum++] = pNode->data[iIndex - 1];
for (i = 0; i < iNode->keyNum; i++)
lNode->data[lNode->keyNum++] = iNode->data[i];
for (i = iIndex - 1; i < pNode->keyNum - 1; i++)
pNode->data[i] = pNode->data[i + 1];
pNode->keyNum--;
//(2) If the iNode has child nodes, it is incorporated into the lNode
if (lNode->childNum > 0) {
for (i = 0; i < iNode->childNum; i++) {
iNode->child[i]->parent = lNode;
lNode->child[lNode->childNum++] = iNode->child[i];
}
}
for (i = iIndex; i < pNode->childNum - 1; i++)
pNode->child[i] = pNode->child[i + 1];
pNode->child[--pNode->childNum] = NULL;
delete iNode;
}else {
/*
rNode Yes, borrow a bit from pNode plus the remaining information of iNode and merge it into rNode
*/
//(1) Pnode - > data [Iindex] and the remaining keywords of iNode are incorporated into rNode
for (i = rNode->keyNum - 1; i >= 0; i--)
rNode->data[i + MIN_KEY_NUM] = rNode->data[i];
rNode->data[i + MIN_KEY_NUM] = pNode->data[iIndex];
rNode->keyNum++;
for (i = 0; i < iNode->keyNum; i++) {
rNode->data[i] = iNode->data[i];
rNode->keyNum++;
}
for (i = iIndex; i < pNode->keyNum - 1; i++)
pNode->data[i] = pNode->data[i + 1];
pNode->keyNum--;
// (2) If the iNode has child nodes, it is incorporated into the rNode
if (iNode->childNum > 0) {
for (i = rNode->childNum - 1; i >= 0; i--)
rNode->child[i + MIN_KEY_NUM] = rNode->child[i];
for (i = 0; i < iNode->childNum; i++) {
iNode->child[i]->parent = rNode;
rNode->child[i] = iNode->child[i];
rNode->childNum++;
}
}
for (i = iIndex; i < pNode->childNum - 1; i++)
pNode->child[i] = pNode->child[i + 1];
pNode->child[--pNode->childNum] = NULL;
delete iNode;
}
if (pNode->parent && pNode->keyNum < MIN_KEY_NUM) {
// When pNode is not the root node and the number of keywords is less than the threshold, its parent nodes and left and right sibling nodes are merged
BTNode* ppNode = pNode->parent;
BTNode *plNode = NULL, *prNode = NULL;
for (i = 0; i < ppNode->childNum; i++)
if (ppNode->child[i] == pNode)
break;
if (i >= 1)
plNode = ppNode->child[i - 1];
if (i <= ppNode->childNum - 1)
prNode = ppNode->child[i + 1];
MergeNode(T, ppNode, plNode, i, prNode);
}
}
return OK;
}
Status DeleteData(BTree &T, Result dPos) {
int pos = dPos.pos;
BTNode* node = dPos.node;
if (node == NULL || pos < 0) {
cout << "Delete error" << endl;
return ERROR;
}else {
if (node->childNum > 0) {
// Node is a non terminal node. Replace it with its precursor, and then delete the keyword of the precursor location
BTNode* preNode = FindLastNode(node->child[pos]);
node->data[pos] = preNode->data[preNode->keyNum - 1];
DeleteData(T, { preNode, preNode->keyNum - 1, DELETE});
}else {
if (node->keyNum > MIN_KEY_NUM) { // If the number of keywords is greater than the threshold, delete them directly
node->keyNum -= 1;
}else { // The number of keywords is less than the threshold. Merge after deletion
for (int i = pos; i < node->keyNum - 1; i++)
node->data[i] = node->data[i + 1];
node->keyNum--;
BTNode* pNode = node->parent;
if (pNode) { // Node is not a root node. It needs to merge parent nodes and left and right sibling nodes
BTNode *lNode = NULL, *rNode = NULL;
int iIndex = 0;
for (; iIndex < pNode->childNum; iIndex++) {
if (pNode->child[iIndex] == node)
break;
}
if (iIndex >= 1)
lNode = pNode->child[iIndex - 1];
if (iIndex <= pNode->childNum - 1)
rNode = pNode->child[iIndex + 1];
MergeNode(T, pNode, lNode, iIndex, rNode);
}
}
}
}
return OK;
}
Status DeleteData(BTree &T, KeyType key) {
Result res = SearchData(T, key);
if (res.tag == FAIL)
return ERROR;
else {
res.tag = DELETE;
DeleteData(T, res);
}
return OK;
}
BTNode* FindLastNode(BTNode* rootNode) {
BTNode* p = rootNode;
while (p->childNum > 0) {
p = p->child[p->childNum - 1];
}
return p;
}
void PrintBTree(BTree T) {
BTNode* p = T;
if (p->childNum == 0) {
for (int i = 0; i < p->keyNum; i++)
cout << p->data[i].key << ",";
}
else {
int i = 0;
for (; i < p->keyNum; i++) {
PrintBTree(p->child[i]);
cout<< p->data[i].key << ",";
}
PrintBTree(p->child[i]);
}
}
3,main.cpp
#include<iostream>
#include"BTree.h"
using namespace std;
int main() {
DataType dataList[15] = { {89}, {92}, {1},{3},{5},{6},{8},{9},{11},{13},{15},{22},{30},{35},{36} };
BTree tree;
InitBTree(tree, dataList, 15);
cout << "B Traversal results after tree initialization:";
PrintBTree(tree);
cout << endl;
DeleteData(tree, 3);
cout << "Traversal result after deleting keyword 3:";
PrintBTree(tree);
cout << endl;
system("pause");
return 0;
}
4. Operation results:
