Introduction

Backpack problems can be divided into:

1. 01 Backpack (Optimized: Reversed)
2. Full Backpack (Optimized: Positive Order)
3. MultiplePack
4. Optimization of Multiple Backpacks

01 Backpack

There are N items and a backpack with a capacity of V.Each item can only be used once.Item i has a volume of vi and a value of wi.
Solve which items are loaded into a backpack so that the total volume of these items does not exceed the backpack volume and the total value is greatest.Output maximum value.

Features: There is only one quantity per item.
Status: dp[i][j] Consider the first I items with space J
No optimization: Layer 2 loop positive sequence dp[i][j] = max(dp[i-1][j], dp[i-1][j-vi]+wi)
Optimize: Layer 2 inverted dp[j] = max(dp[j], dp[j-vi]+wi)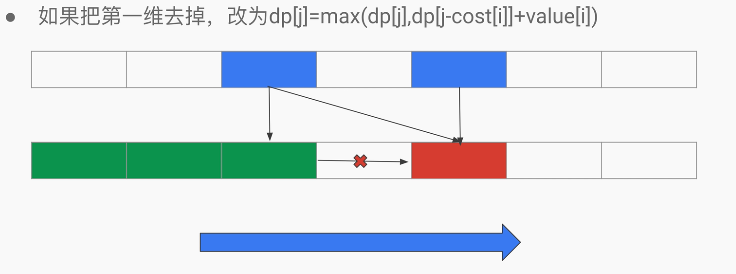

n, v = map(int, input().split())
dp = [0]*(v+1)
for i in range(n):
    a,b = map(int, input().split())
    for j in range(v, a-1, -1):
        dp[j] = max(dp[j], dp[j-a]+b)
res = 0
print(dp[v]) 

Full Backpack

The number of each item in the backpack is infinite and can be picked up repeatedly.
No spatial optimization: dp[i][j] = max(dp[i-1][j], dp[i][j-vi]+wi) Note that the latter item is dp[i] transferred.
Spatial optimization: second-order, dp[j] = max(dp[j], dp[j-vi]+wi)

n, v = map(int, input().split())
goods = []
for i in range(n):
    goods.append([int(i) for i in input().split()])
'''    
dp = [[0]*(v+1) for _ in range(n)]
for i in range(n):
    for j in range(1, v+1):
        if goods[i][0]<=j:
            # Note here at 01 the backpack is different, here is the transfer from DP[i][j-k]
            dp[i][j] = max(dp[i-1][j], dp[i][j-goods[i][0]] + goods[i][1])
        else:
            dp[i][j] = dp[i-1][j]
           
res = 0
for i in range(v+1):
    res = max(res, dp[n-1][i])
'''
dp = [0]*(v+1)
for i in range(n):
    for j in range(goods[i][0],v+1):
        dp[j] = max(dp[j], dp[j-goods[i][0]]+goods[i][1])

res = 0
for i in range(1, v+1):
    res = max(res, dp[i])
print(res)

MultiplePack

The number of items in the backpack is limited.The idea for this type of problem is to convert to a 01 backpack problem (compressed space, traversed in reverse order).

Method 1. Violence enumeration, considering 1, 2 at a time.n items into Backpack

# Design a triple loop,
# First Incremental Enumeration Range
# Layer 2 Decreasing, Type of 01 Backpack
# Number of additions to the third layer enumeration
n, v = map(int, input().split())

dp = [0]*(v+1)
for i in range(n):
    a, b, c = map(int, input().split())
    for j in range(v, a-1, -1):
        for k in range(1, min(c, j//a)+1):
            dp[j] = max(dp[j], dp[j-k*a]+k*b)
print(dp[-1])

• Time Complexity: O(n_k)O(n*Sigma k)O(n_k)

Method 2. Disassemble several items, and divide them according to binary system, that is, one, two, four, leaving k in a separate group.New 01 Backpack Problem

# This question is more complex than the previous one.
N, V = map(int, input().split())
goods = []
for i in range(N):
    v,w,s = map(int, input().split())
    k = 1
    while True:
        s -= k
        if s<0:
            s += k
            break
        goods.append([v*k,w*k])
        k *= 2
    if s>0:
        goods.append([v*s, w*s])

n = len(goods)
dp = [0]*(V+1)
for i in range(n):
    for j in range(V, goods[i][0]-1, -1):
        dp[j] = max(dp[j], dp[j-goods[i][0]]+goods[i][1])
print(dp[-1])

• Time complexity: O(N_log_2(K)) O(N*Sigmalog_2(K)) O(N_log2(K))

Method 3. Use a limited queue and categorize items
Reduce time complexity to O(NV)O(NV)O(NV)

import collections
N=20001
dp=[0]*N
[n,m]=map(int,input().split())
q = collections.deque()
for i in range(n):
    [v,w,s]= map(int,input().split())
    for j in range(v):
        q.clear()  # Note that the queue needs to be initialized for each new loop
        stop=(m-j)//v  # There is room left for up to a few current items
        for k in range(0,stop+1):
            val = dp[k*v+j]-k*w
            while q and val>=q[-1][1]:
                q.pop()
            q.append([k,val])
            if q[0][0]<k-s:  # The number of items stored should not exceed the number of items, otherwise pop up
                q.popleft()
            dp[v*k+j] = q[0][1]+k*w
    #print(dp)
print(dp[m])