Backtracking algorithm is actually a similar exhaustive search attempt process, which is mainly to find the order of the problem in the search attempt process. When it is found that the solution conditions are not met, it will "backtrack" (i.e. backtrack) and try other paths. Therefore, backtracking method is known as "common problem-solving method".
Go along the same road. If you can go in, go in. If you can't go in, go back. Try another way.
Application of backtracking algorithm:
Question 1: Full Permutation Problem:
Solve the problem of full arrangement of all characters in string "ABC" (excluding repetition)
ABC ACB BAC CAB CBA
All permutations for the string "ABB"
ABB BAB BBA
Problem analysis:
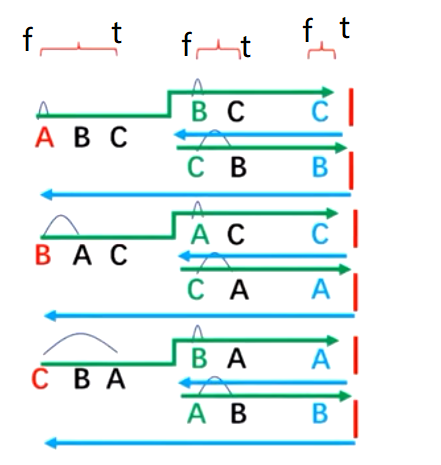As shown in the figure: first, the string is immutable. We can format the string into an array. F represents the subscript of the first element of the array, and T represents the subscript of the last element of the array. We exchange the character in position f with the character in the first position, and then move f back one position, and then we operate the character from position f + 1 to position t immediately above. The condition for stopping recursion is when f==t
The code is as follows:
import java.util.HashSet;
public class FullPermutation {
public static void main(String[] args) {
String s = "ABC";
char[] arr = s.toCharArray(); //Format the string into an array. Easy to modify
HashSet<String> set = new HashSet<>(); //Weight removal (Hashset has its own weight removal effect)
//Define a method to implement the function
/*
Store the correct sort into the set, and Hashset will automatically filter out duplicate elements
Operate on the character array to filter out the qualified characters
The range of characters to filter
*/
Permutation(set, arr, 0, arr.length - 1);
System.out.println(set);
}
private static void Permutation(HashSet<String> set, char[] arr, int from, int to) {
if(from == to){
set.add(String.valueOf(arr)); //Format the character array as A string [A, B, C] = > "ABC"
}else {
for (int i = from; i <= to; i++) {
swap(arr, i, from);
Permutation(set, arr, from + 1, to) ;
//Pay attention to switching back after each exchange
swap(arr, i, from);
}
}
}
private static void swap(char[] arr, int i, int j) {
char temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}Operation results: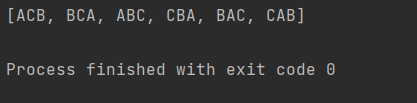
Question 2: maze problem
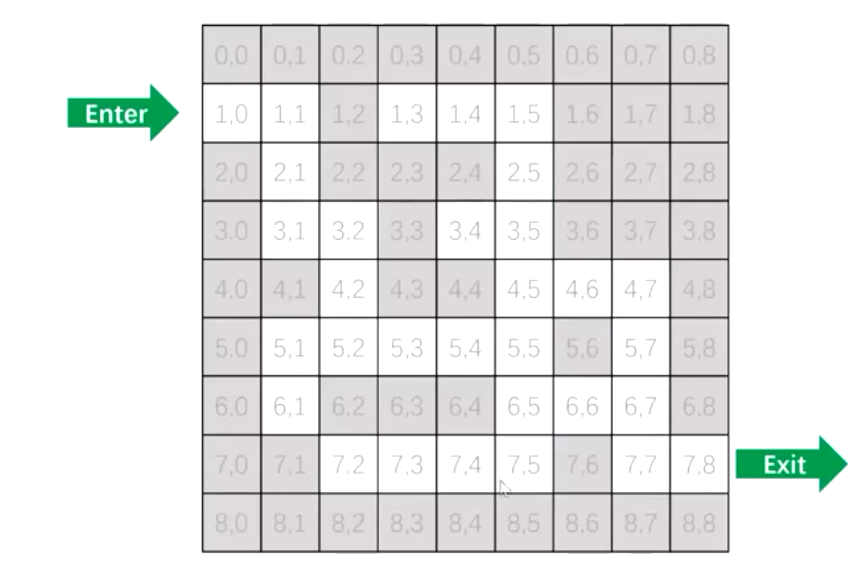
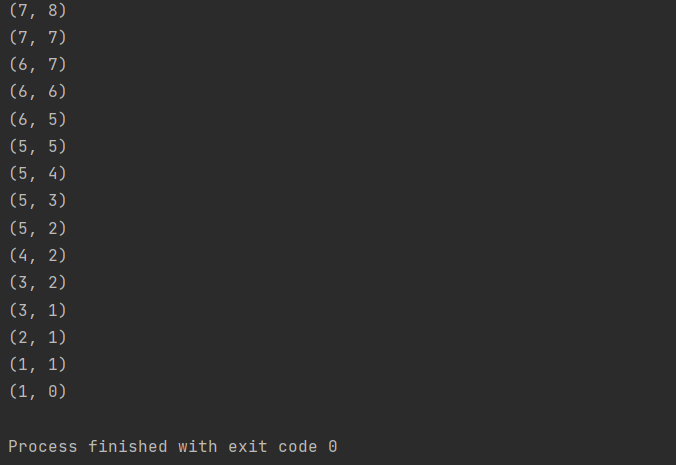
We want to go from (1,0) to (7,8). We can set the starting point coordinate to (1,0), then make "1" as the wall and "0" as the road, and then let the coordinates of the current point traverse in the order of "top right, bottom left" to find the road, When encountering a dead end, we can go back (we can create a stack to store the route, bounce the stack when we go back, and enter the stack when we find the route). When going back, we should make a mark at the position where we go back to prevent dead circulation (we can create a Boolean type two-dimensional array and mark true at the position where we go back). Finally, we output the stack. If we find the way, we output the content of the station, otherwise we output "maze impassability".
The code is as follows:
import java.util.LinkedList;
public class Maze {
private static int[][] maze = {
{1, 1, 1, 1, 1, 1, 1, 1, 1},
{0, 0, 1, 0, 0, 0, 1, 1, 1},
{1, 0, 1, 1, 1, 0, 1, 1, 1},
{1, 0, 0, 1, 0, 0, 1, 1, 1},
{1, 1, 0, 1, 1, 0, 0, 0, 1},
{1, 0, 0, 0, 0, 0, 1, 0, 1},
{1, 0, 1, 1, 1, 0, 0, 0, 1},
{1, 1, 0, 0, 0, 0, 1, 0, 0},
{1, 1, 1, 1, 1, 1, 1, 1, 1}
};
//Entry information
private static int entryX = 1;
private static int entryY = 0;
//Export information;
private static int exitX = 7;
private static int exitY = 8;
//Path access status table
private static boolean[][] vistied = new boolean[9][9];
//Change in direction
private static int[][] direction = {{1,0}, {0, 1}, {0, -1}, {-1, 0}};
//Stack of storage paths
private static LinkedList<String> stack = new LinkedList<>();
public static void main(String[] args) {
boolean flag = go(entryX, entryY);
if (flag){
for (String path: stack){
System.out.println(path);
}
}else {
System.out.println("The maze is impassable!");
}
}
private static boolean go(int entryX, int entryY) {
stack.push("(" + entryX + ", " + entryY + ")");
vistied[entryX][entryY] = true;
if (entryX == exitX && entryY == exitY){
return true;
}
//Consider four directions: up, right, down and left
for (int i = 0; i < direction.length; i++) {
int newX = direction[i][0] + entryX;
int newY = direction[i][1] + entryY;
if (isLnArea(newX, newY) && isRoad(newX, newY) && !vistied[newX][newY]){
if (go(newX,newY)){
return true; // If a direction can pass, return true upward, indicating that X and y of this level can pass
}
}
}
stack.pop();
return false; //If the four directions are blocked, put back false upward, indicating that X and y of this level are blocked
}
private static boolean isRoad(int newX, int newY) {
return maze[newX][newY] == 0;
}
private static boolean isLnArea(int newX, int newY) {
return newX >=0 && newX <9 && newY >= 0 && newY < 9;
}
}
Operation results:
Question 3: eight queens question:
In an 8X8 chessboard, put 8 pieces of queens. It is required that there should be no duplicate pieces of queens in the same column and slash.
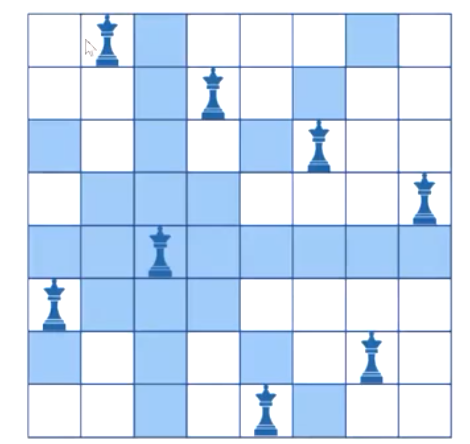
We take the first position of the chessboard as the starting point, and then use the column to traverse. When we traverse, we add judgment to judge whether the position can put chess pieces. When one row of the chessboard is placed, we traverse the next row (row indicates row and col indicates column). When we traverse to a certain row, we find that no chess pieces can be placed in each column, and then we go back to the previous row, Let the previous line go down. Until row reaches the outside of the chessboard, it stops recursion.
The code is as follows:
public class NQueen {
private static int count = 0;//Record the number of solutions
private static final int N = 8; //Size of N-queen matrix
private static int[][] arr = new int[N][N];//Chessboard data 0 means empty and 1 means queen
public static void main(String[] args) {
queen(0);
}
//Recursively solve the problem of row subscript line queen. If row == N, it means that a solution comes out, and row is traversed from 0
private static void queen(int row) {
if (row == N){
count++;
System.out.println("The first" + count + "Solutions:");
printArr();
}else {
//Traverse the current column
for (int col = 0; col < N; col++) {
//Judge whether the position of this point conflicts with the pieces in other positions
if (!isDangerous(row, col)){
//Every time you want to place the queen, empty the diversion first
for (int c = 0; c < N; c++){
arr[row][c] = 0;
}
arr[row][col] = 1;
queen(row + 1);
}
}
}
}
private static void printArr() {
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
System.out.print(arr[i][j] + " ");
}
System.out.println();
}
}
private static boolean isDangerous(int row, int col) {
//Upward
for (int r = row - 1; r >= 0; r--) {
if (arr[r][col] == 1){
return true;
}
}
//Left up
for (int r = row - 1, c = col - 1 ; r >=0 && c >= 0; r--, c--) {
if (arr[r][c] == 1){
return true;
}
}
//Upper right
for (int r = row - 1, c = col + 1; r >= 0 && c < N; r--, c++){
if (arr[r][c] == 1){
return true;
}
}
return false;
}
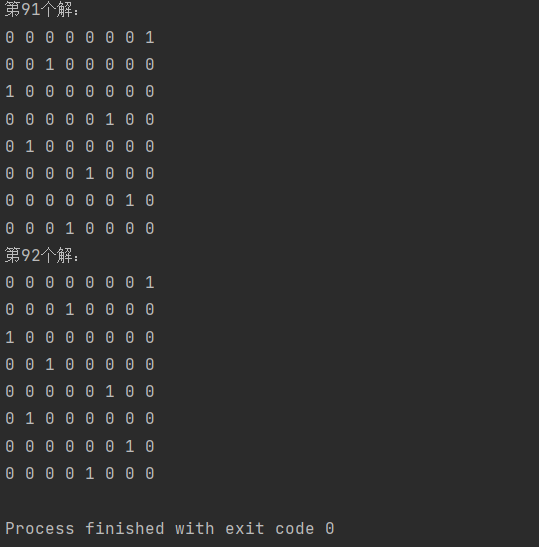
}Output result:
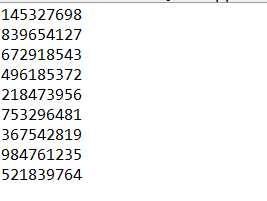
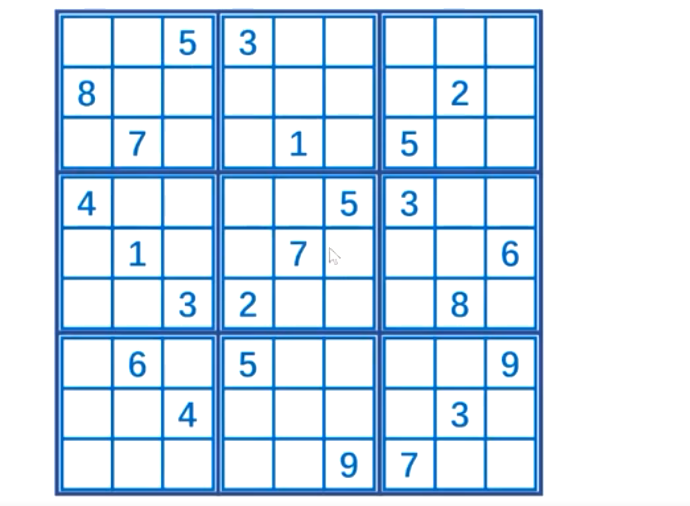
Question 4: Sudoku
The numbers in each row, column and thick line Palace (3X3) contain 1 ~ 9 and are not repeated
Solution: similar to the eight queens problem, take the first point as the starting point and traverse from 1 to 9 to see whether the numbers in each row, column and thick line Palace (3X3) are repeated. If 1 to 9 are repeated, go back up, let the previous grid then traverse the following numbers, and fill in the grid if they are not repeated. When there are numbers in the grid, skip directly
The code is as follows:
package p4.Divide and conquer backtracking;
import java.io.*;
//Sudoku
public class Sudoku {
private static int i = 0;
private static int[][] board = new int[9][9];
public static void main(String[] args) throws IOException {
readFile("sudoku_data_01.txt");
solve(0, 0);
}
//Solve the solution of x-y lattice, and then continue to solve the next lattice recursively
//Essence seeks multiple solutions, but the actual Sudoku problem can only have one solution. If there is no solution, the program will not output anything!
private static void solve(int row, int col) {
if (row == 9) {
i++;
System.out.println("===========" + i + "==========");
printBoard();
//System.exit(0);
} else {
if (board[row][col] == 0) {
//You need to fill in numbers 1 ~ 9
for (int num = 1; num <= 9; num++) {
if (!isExist(row, col, num)) {
board[row][col] = num; //8
//Solve the next grid
solve(row + (col + 1) / 9, (col + 1) % 9);
}
//If there is no solution here, it must be cleared
board[row][col] = 0;
}
} else {
//There is already a known number. Jump directly to the next grid
solve(row + (col + 1) / 9, (col + 1) % 9);
}
}
}
private static boolean isExist(int row, int col, int num) {
//Peer
for (int c = 0; c < 9; c++) {
if (board[row][c] == num) {
return true;
}
}
//Same column
for (int r = 0; r < 9; r++) {
if (board[r][col] == num) {
return true;
}
}
//Same as Jiugong 3 * 3
int rowMin = 0;
int colMin = 0;
int rowMax = 0;
int colMax = 0;
if (row >= 0 && row <= 2) {
rowMin = 0;
rowMax = 2;
}
if (row >= 3 && row <= 5) {
rowMin = 3;
rowMax = 5;
}
if (row >= 6 && row <= 8) {
rowMin = 6;
rowMax = 8;
}
if (col >= 0 && col <= 2) {
colMin = 0;
colMax = 2;
}
if (col >= 3 && col <= 5) {
colMin = 3;
colMax = 5;
}
if (col >= 6 && col <= 8) {
colMin = 6;
colMax = 8;
}
for (int r = rowMin; r <= rowMax; r++) {
for (int c = colMin; c <= colMax; c++) {
if (board[r][c] == num) {
return true;
}
}
}
return false;
}
private static void readFile(String fileName) throws IOException {
File file = new File(fileName);
FileReader fr = new FileReader(file);
BufferedReader br = new BufferedReader(fr);
String line = null;
int row = 0;
while ((line = br.readLine()) != null) {
for (int col = 0; col < 9; col++) {
board[row][col] = Integer.parseInt(line.charAt(col) + "");
}
row++;
}
}
private static void printBoard() {
for (int i = 0 ; i < 9; i++) {
for (int j = 0; j < 9; j++) {
System.out.print(board[i][j] + " ");
}
System.out.println();
}
}
}Text document content:
Execution results:
