Source: Code Capriccio
Link of force buckle in this question: https://leetcode-cn.com/problems/combination-sum/

1. Title Description:

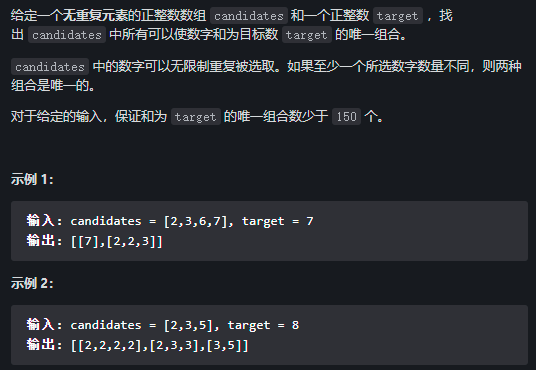
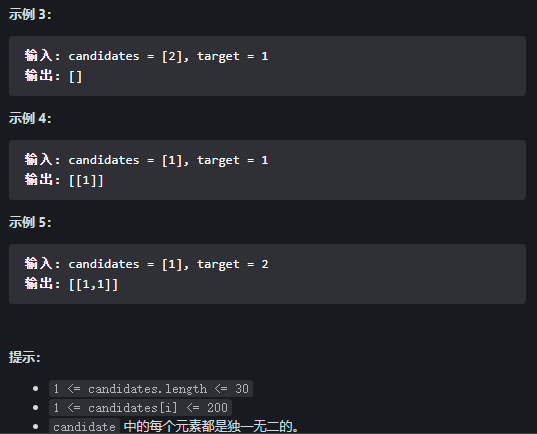
2. Idea:

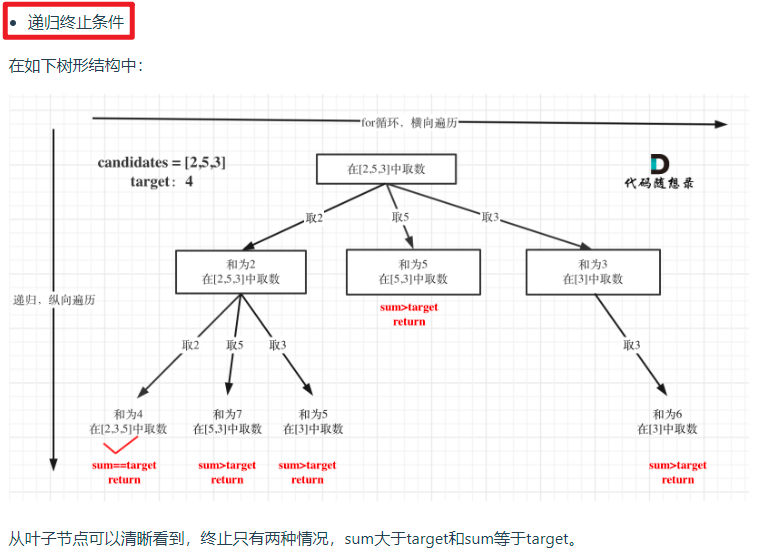
The difference between this question and the question of seeking combination is that this question has no quantitative requirements and can be limited to repetition, but it has the limit of sum, so there is also the limit of number indirectly. The search process of this question is abstracted into a tree structure as follows:

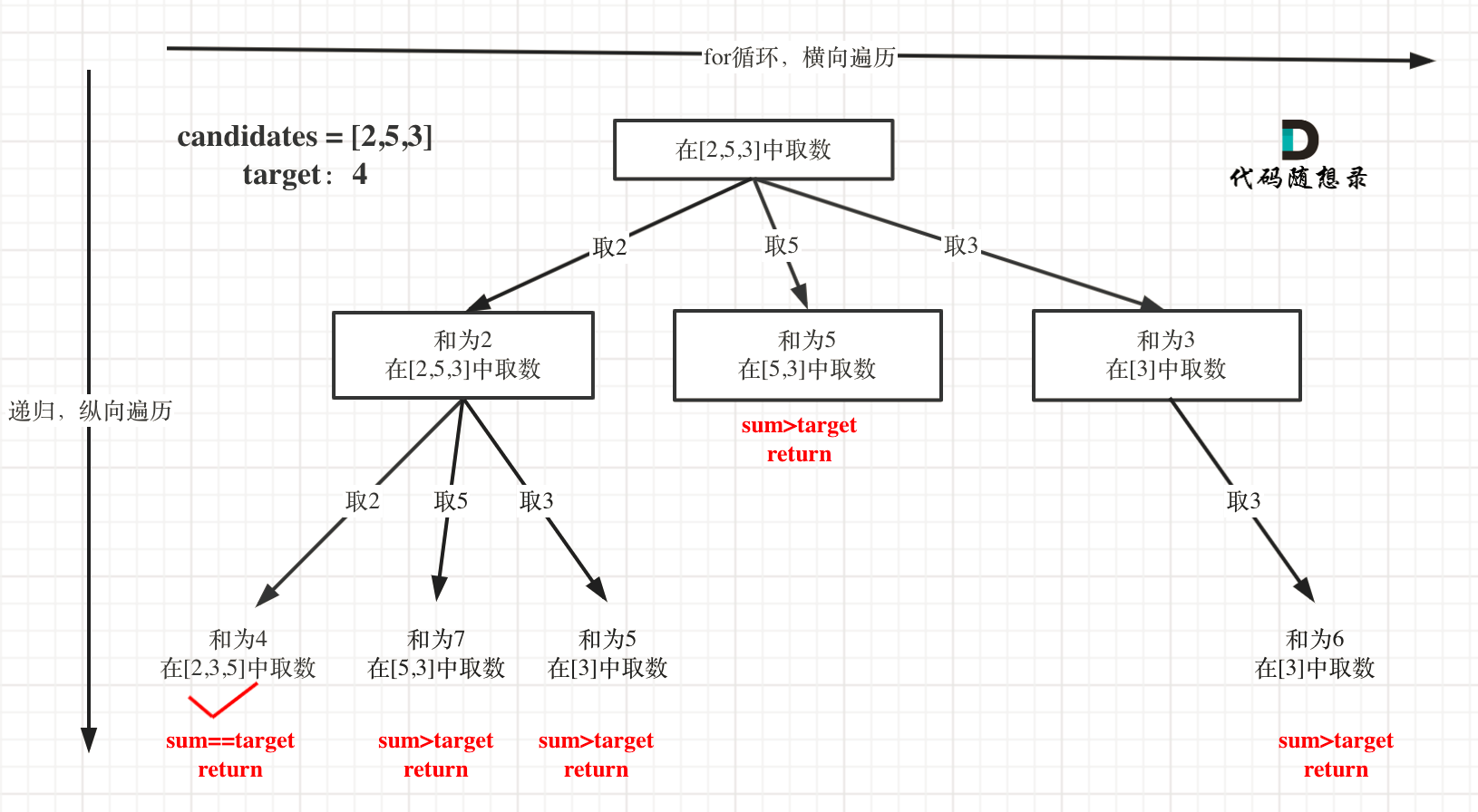
Here I need to say one more thing:
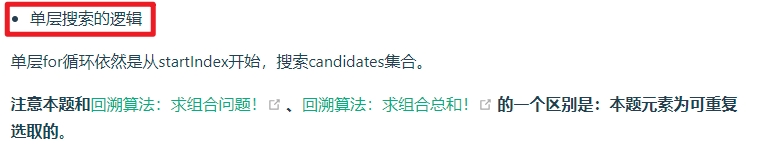
This problem is different from the previous combinatorial problem. The previous combinatorial problem cannot be repeated, while the same elements of this problem can be repeated. From the tree, the first node of each layer uses all the elements, and the subsequent nodes subtract the previous elements.
Therefore, we only need to modify it in the for loop (because horizontal for traversal and vertical recursion).

Still press the recursive Trilogy:

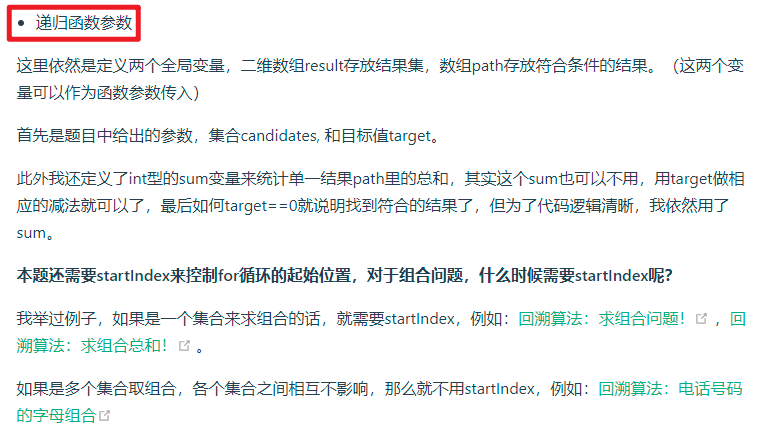
3. Code:

3.1 python code:

• (1) The first thing I think of is: duplicate combined sets, and then sort them when saving to ensure that the combined sets are added only once. However, this method obviously has high time complexity. Just record it. Here is the code:

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        res = [] # Store result set
        path = [] # Collect elements on path
        def backtracking(index):
            if sum(path) == target:
                temp = path.copy()
                temp.sort() # Sort the qualified permutations from small to small
                if temp not in res: # Filter repeated permutations, that is, a combination
                    res.append(temp)
                return
            for i in range(len(candidates)):
                if sum(path) < target:
                    path.append(candidates[i]) # Elements on collection path (processing)
                    backtracking(index+1) # recursion
                    path.pop() # to flash back
                else: # Terminate traversal
                	break
        
        backtracking(0)
        return res

• (2) Directly generate non repeated combinations: note the parameter startIndex. In combinations, the parameter startIndex controls the non repeated selection of elements

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        res = [] # Store result set
        path = [] # Collect elements on path
        def backtracking(startIndex):
            if sum(path) == target:
                res.append(path.copy())
                return
            for i in range(startIndex, len(candidates)):
                if sum(path) < target: # This judgment is a pruning operation
                    path.append(candidates[i]) # Elements on collection path (processing)
                    backtracking(i) # Recursion, without i+1, the current element can be retrieved repeatedly
                    path.pop() # to flash back
                else: # Terminate traversal
                	break
        
        backtracking(0)
        return res

3.2 C + + Code:

• (1) Uncut Code:

class Solution {
private:
    vector<vector<int>> res; // Store the final result set
    vector<int> path; // Collect valid values on the tree path
    void backtracking(vector<int>& candidates, int target, int startIndex, int sum){
        if(sum > target){
            return;
        }
        if(sum == target){
            res.push_back(path);
            return;
        }
        for(int i = startIndex; i < candidates.size(); i++){
            sum += candidates[i];
            path.push_back(candidates[i]); // Collect elements on path
            backtracking(candidates, target, i, sum); // If i+1 is not used, it means that the element can be reused
            sum -= candidates[i]; // to flash back
            path.pop_back(); // to flash back
        }
    }

public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        // sort(candidates.begin(), candidates.end()); //  Sort required (pruning required)
        backtracking(candidates, target, 0, 0);
        return res;

    }
};

• (2) Code after pruning: it needs to be sorted first, because it is sorted from small to large. As long as the sum is greater than the target, the following code must be greater than. If it is not sorted, it is not necessarily.

class Solution {
private:
    vector<vector<int>> res; // Store the final result set
    vector<int> path; // Collect valid values on the tree path
    void backtracking(vector<int>& candidates, int target, int startIndex, int sum){
        if(sum > target){
            return;
        }
        if(sum == target){
            res.push_back(path);
            return;
        }
        for(int i = startIndex; i < candidates.size() && (sum + candidates[i]) <= target; i++){
            sum += candidates[i];
            path.push_back(candidates[i]); // Collect elements on path
            backtracking(candidates, target, i, sum); // If i+1 is not used, it means that the element can be reused
            sum -= candidates[i]; // to flash back
            path.pop_back(); // to flash back
        }
    }

public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        sort(candidates.begin(), candidates.end()); // You need to sort and prune
        backtracking(candidates, target, 0, 0);
        return res;

    }
};

4. Summary:

This problem is still a combinatorial problem. Different from the most basic combinatorial problem, the combinatorial elements of this problem can be repeated.
Pay special attention to the parameter startIndex, which is used to control the starting position of the for loop. When do you need to use the parameter startIndex?
Answer:
1) To find the combination of a set, you must use the startIndex parameter;
2) If multiple sets are combined and each set does not affect each other, there is no need to use the startIndex parameter.