Binary tree definition:
Binary tree (English: binary tree) is a tree structure with at most two branches per node (i.e. there are no nodes with branching degree greater than 2). Branches are usually called "left subtree" or "right subtree". The branches of binary tree have left-right order and cannot be reversed at will. For more explanations, see Heap and heap sorting.
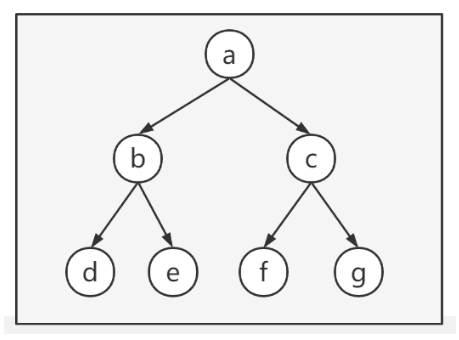
1, Recursive traversal
1. Preorder traversal
Root left and right. a,b,d,e,c,f,g
/**
* Binary tree: preorder traversal. Root left right
*
* Classical recursive writing
*
* @author Java And algorithm learning: Monday
*/
public static void pre(Node head) {
if (head == null) {
return;
}
System.out.println(head.value);
pre(head.left);
pre(head.right);
}
2. Medium order traversal
Left root right. d,b,e,a,f,c,g
/**
* Binary tree: medium order traversal. Left root right
*
* Classical recursive writing
*
* @author Java And algorithm learning: Monday
*/
public static void in(Node head) {
if (head == null) {
return;
}
in(head.left);
System.out.println(head.value);
in(head.right);
}
3. Postorder traversal
Left and right roots. d,e,b,f,g,c,a
/**
* Binary tree: post order traversal. Left right root
*
* Classical recursive writing
*
* @author Java And algorithm learning: Monday
*/
public static void pos(Node head) {
if (head == null) {
return;
}
pos(head.left);
pos(head.right);
System.out.println(head.value);
}
We are familiar with the classic recursive version of preorder, middle order and postorder traversal. Today we talk about some different, recursive order.
Careful little friends seem to have found that recursive preorder, middle order and postorder traversal are actually very similar, that is, the printing time is different. This is because they are actually rewritten by recursive order. What is a recursive order is to print the value of the node every time you pass by yourself. The last printed out is the recursive order.
On the basis of recursive order, only the value when it passes through itself for the first time is printed, that is, the first order; Print only the values that pass through you for the second time, that is, the middle order; Only the values that have passed the third time are printed, which is the post order.
4. Recursive order
/**
* Recursive order
*
* @author Java And algorithm learning: Monday
*/
public static void f(Node head) {
if (head == null) {
return;
}
// 1
System.out.println(head.value);
f(head.left);
// 2
System.out.println(head.value);
f(head.right);
// 3
System.out.println(head.value);
}
A conclusion: given the preorder traversal and postorder traversal of a binary tree, for a node x, the node set before x preorder traversal is a, and the node set after X postorder traversal is B, then the intersection of a and B must be all the ancestor nodes of node X.
2, Non recursive traversal
1. Preorder traversal
(1) Prepare a stack and push in the current node (i.e. the head node)
(2) Pop up the stack top element and print the corresponding value
(3) This element has a right child pushing the right child into the stack, and a left child pushing the left child into the stack (first right and then left)
(4) Perform steps 2 and 3 until the stack is empty.
/**
* Non recursive preorder traversal
*
* @author Java And algorithm learning: Monday
*/
public static void pre(Node head) {
if (head != null) {
Stack<Node> stack = new Stack<>();
//Push in current node
stack.push(head);
while (!stack.isEmpty()) {
//Pop up stack top element
Node current = stack.pop();
System.out.print(current.value + " ");
//Press in the right child first, then the left child
if (current.right != null) {
stack.push(current.right);
}
if (current.left != null) {
stack.push(current.left);
}
}
}
}
2. Medium order traversal
(1) Prepare a stack
(2) Press in the entire left subtree with the current node current as the head node (if you stack one, current will move to the left child) until it is empty
(3) Pop up the top element of the stack, print its value, take the right child of the current pop-up element as the current node, and repeat step 2
(4) End when stack is empty
/**
* Non recursive middle order traversal
*
* @author Java And algorithm learning: Monday
*/
public static void in(Node head) {
if (head != null) {
Stack<Node> stack = new Stack<>();
Node current = head;
while (!stack.isEmpty() || current != null) {
if (current != null) {
//Stack the entire left subtree of the current node
stack.push(current);
current = current.left;
} else {
//After the left subtree is stacked, the stack top element pops up
Node pop = stack.pop();
System.out.print(pop.value + " ");
//Take the right child of the current pop-up element as the current node and continue the cycle
current = pop.right;
}
}
}
}
3. Postorder traversal
(1) Prepare two stacks, stackA and stackB, and push stackA into the current node (i.e. the head node)
(2) Pop up the stack top element and press into stackB
(3) This element has a left child pressing the left child into the stackA stack, and a right child pressing the right child into the stackA stack (first left and then right)
(4) Continue to perform steps 2 and 3 until the stackA stack is empty.
(5) Print all stackB stack elements
It is equivalent to that the stack order of stackA is right and left, and the stack order of stackB is left and right.
/**
* Non recursive postorder traversal
*
* @author Java And algorithm learning: Monday
*/
public static void pos(Node head) {
if (head != null) {
Stack<Node> stackA = new Stack<>();
Stack<Node> stackB = new Stack<>();
stackA.push(head);
while (!stackA.isEmpty()) {
//stackA stack order is , right , left
Node current = stackA.pop();
//The stacking order of stackbis , root , right , left
stackB.push(current);
//Stack a: first the left child enters the stack, and then the right child enters the stack
if (current.left != null) {
stackA.push(current.left);
}
if (current.right != null) {
stackA.push(current.right);
}
}
//Stackbthe stack order is , left , right , root
while (!stackB.isEmpty()) {
System.out.print(stackB.pop().value + " ");
}
}
}
3, Binary tree traversal by layer
(1) Prepare a queue, and the head node joins the queue
(2) Print the value of a node out of the queue; if there is a left child in the out of the queue node, the left child will join the team, and if there is a right child, the right child will join the team
(3) Loop through step 2 until the queue is empty
/**
* Binary tree traversal by layer
*
* @author Java And algorithm learning: Monday
*/
public static void levelTraversal(Node head) {
if (head == null) {
return;
}
//Prepare a queue
Queue<Node> queue = new LinkedList<>();
//Head node queue
queue.offer(head);
while (!queue.isEmpty()) {
//Pop a node from the queue
Node current = queue.poll();
//Print
System.out.print(current.value + " ");
//If there is a left child, the left child joins the team
if (current.left != null) {
queue.offer(current.left);
}
//If there is a right child, the right child will join the team
if (current.right != null) {
queue.offer(current.right);
}
}
}
This paper mainly introduces the recursive traversal (and the previously unknown recursive order), non recursive traversal and sequence traversal of binary tree.