In the previous chapter, we talked about 10 common data structures, and then we talked about 10 common algorithms.
Address of the previous chapter: Foundation compaction: Basic data structure and algorithm (I) , you can have a look if you don't know much.
10 common algorithms
The content of data structure research is how to organize the data according to a certain logical structure, select an appropriate storage representation method, and store the data organized by the logical structure in the computer memory.
The purpose of algorithm research is to process data more effectively and improve data operation efficiency. Data operation is defined in the logical structure of data, but the specific implementation of operation should be carried out in the storage structure.
Generally, there are the following common operations:
- Retrieval: retrieval is to find nodes that meet certain conditions in the data structure. Generally, given the value of a field, find the node with the value of the field.
- Insert: adds a new node to the data structure.
- Delete: removes the specified node from the data structure.
- Update: changes the value of one or more fields of the specified node.
- Sort: rearrange nodes in a specified order. For example, increasing or decreasing.
1. Recursive algorithm
Recursive algorithm: it is an algorithm that directly or indirectly calls itself. In computer programming, recursive algorithm is very effective to solve a large class of problems. It often makes the description of the algorithm concise and easy to understand.
Recursive processes are generally implemented by functions or subprocesses.
The essence of recursive algorithm is to transform the problem into a sub problem of the same kind of problem with reduced scale. Then recursively call the function (or procedure) to represent the solution of the problem.
Features of recursive algorithm for solving problems:
- Recursion is to call itself in a procedure or function.
- When using recursion strategy, there must be an explicit recursion end condition, which is called recursion exit.
- Recursive algorithm is usually very concise, but the operation efficiency of recursive algorithm is low. Therefore, it is generally not advocated to design programs with recursive algorithms.
- In the process of recursive call, the system opens up a stack for the return point and local quantity of each layer. Too many recursions are easy to cause stack overflow and so on. Therefore, it is generally not advocated to design programs with recursive algorithms.
Let's analyze the working principle of recursion in detail.
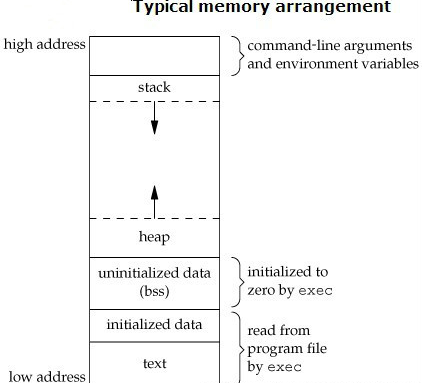
Let's take a look at the execution mode of functions in C language. We need to know something about the organization of C programs in memory:
The heap grows upward from low address to high address, while the stack grows in the opposite direction (the actual situation is related to the CPU architecture).
When a function is called in the C program, a space is allocated in the stack to store information related to the call, and each call is regarded as active.
The storage space on the stack is called active record or stack frame.
The stack frame consists of five areas: input parameters, return value space, temporary storage space used to calculate expressions, state information saved during function calls, and output parameters. See the figure below:
Stack is an excellent scheme for storing function call information. However, stack also has some disadvantages:
The stack maintains the information of each function call until the function returns, which takes up a lot of space, especially when many recursive calls are used in the program.
In addition, because there is a large amount of information to be saved and recovered, it takes some time to generate and destroy active records.
We need to consider adopting an iterative scheme. Fortunately, we can use a special recursive method called tail recursion to avoid these shortcomings mentioned above.
Example 1: calculate n!
To calculate the factorial of n, the mathematical formula is:
n!=n×(n-1)×(n-2)......2×1
Recursion can be defined as:

The factorial function is realized recursively:
#define _CRT_SECURE_NO_WARNINGS / / avoid scanf errors
#include <stdio.h>
int main(void)
{
int sumInt = fact(3);
printf("3 The factorial of is:%d\n", sumInt);
system("PAUSE");//End without exiting
}
//Recursive factorization
int fact(int n) {
if (n < 0)
return 0;
else if (n == 0 || n == 1)
return 1;
else
return n * fact(n - 1);
}

Example 2: Fibonacci sequence
#define _CRT_SECURE_NO_WARNINGS / / avoid scanf errors
#include <stdio.h>
void main(void)
{
printf("%d \n", fibonacci(10));
system("PAUSE");//End without exiting
}
//Fibonacci sequence, the first two terms are 1; Each of the following items is the sum of the first two items
int fibonacci(int a){
if (a == 1 || a == 2)
{
return 1;
}
else{
return fibonacci(a - 1) + fibonacci(a - 2);
}
}
Example 3: recursively convert an integer number to a string
#define _CRT_SECURE_NO_WARNINGS / / avoid scanf errors
#include <stdio.h>
void main(void)
{
char str[100];
int i;
printf("enter a integer:\n");
scanf("%d", &i);
toString(i, str);
puts(str);
system("PAUSE");//End without quitting
}
//Recursively converts an integer number to a string
int toString(int i, char str[]){
int j = 0;
char c = i % 10 + '0';
if (i /= 10)
{
j = toString(i, str) + 1;
}
str[j] = c;
str[j + 1] = '\0';
return j;
}
Example 4: Tower of Hanoi
#define _CRT_SECURE_NO_WARNINGS / / avoid scanf errors
#include <stdio.h>
//Recursive Hanoi Tower
void hanoi(int i, char x, char y, char z){
if (i == 1){
printf("%c -> %c\n", x, z);
}
else{
hanoi(i - 1, x, z, y);
printf("%c -> %c\n", x, z);
hanoi(i - 1, y, x, z);
}
}
void main(void)
{
hanoi(10, 'A', 'B', 'C');
system("PAUSE");//End without exiting
}
Example 5: monkeys eat peaches
#define _CRT_SECURE_NO_WARNINGS / / avoid scanf errors
#include <stdio.h>
//Monkeys eat peaches, eat half a day and one more, and there is only one left when they want to eat on the tenth day
int chitao(int i){
if (i == 10){
return 1;
}
else{
return (chitao(i + 1) + 1) * 2;
}
}
void main(void)
{
printf("%d", chitao(5));
system("PAUSE");//End without exiting
}
Example 6: Queen N problem
#define _CRT_SECURE_NO_WARNINGS / / avoid scanf errors
#include <stdio.h>
/*======================N Queen problem========================*/
#define N 100
int q[N];//Column coordinates
//Output results
void dispasolution(int n)
{
static int count = 0;
printf(" The first%d A solution:", ++count);
for (int i = 1; i <= n; i++)
{
printf("(%d,%d) ", i, q[i]);
}
printf("\n");
}
//Judge whether the position (i,j) can be placed
int place(int i, int j)
{
//The first queen can always put
if (i == 1)
return 1;
//Other Queens can't walk in the same row or diagonal
int k = 1;
//k~i-1 is the row where the queen has been placed
while (k < i)
{
if ((q[k] == j) || (abs(q[k] - j) == abs(i - k)))
return 0;
k++;
}
return 1;
}
//Place queen
void queen(int i, int n)
{
if (i > n)dispasolution(n);
else
{
for (int j = 1; j <= n; j++)
{
if (place(i, j)==1)
{
q[i] = j;
queen(i + 1, n);
}
}
}
}
int main()
{
queen(1, 4);
system("PAUSE");//End without quitting
}
2. Sorting algorithm

Sorting is a common operation in programming. Beginners often only know bubble sorting algorithm. In fact, there are many more efficient sorting algorithms, such as Hill sorting, quick sorting, cardinal sorting, merge sorting and so on.
Different sorting algorithms are suitable for different scenarios. Finally, this chapter analyzes various sorting algorithms from the aspects of time performance and algorithm stability.
Sorting algorithm is also divided into internal sorting algorithm and external sorting algorithm. The difference between the former is that the former completes sorting in memory, while the latter needs the help of external memory.
The internal sorting algorithm is introduced here.
Bubble sort:
Bubble sort, also known as "bubble sort", the core idea of the algorithm is to compare all records in the unordered table by pairing keywords to obtain ascending sequence or descending sequence.
For example, the specific implementation process of ascending sorting the unordered table {49, 38, 65, 97, 76, 13, 27, 49} is shown in Figure 1:

The following bubble sorting example
#define _CRT_SECURE_NO_WARNINGS / / avoid scanf errors
#include <stdio.h>
//Bubble sorting
//A function of exchanging the positions of a and b
void swap(int *a, int *b);
void main()
{
int array[8] = { 49, 38, 65, 97, 76, 13, 27, 49 };
int i, j;
int key;
//As many records as there are, you need to bubble as many times. When all records are arranged in ascending order during the comparison process, the sorting ends
for (i = 0; i < 8; i++){
key = 0;//Before starting bubbling each time, the initialization key value is 0
//Each bubbling starts with subscript 0 and ends at 8-i
for (j = 0; j + 1<8 - i; j++){
if (array[j] > array[j + 1]){
key = 1;
swap(&array[j], &array[j + 1]);
}
}
//If the key value is 0, the sorting of records in the table is completed
if (key == 0) {
break;
}
}
for (i = 0; i < 8; i++){
printf("%d ", array[i]);
}
system("PAUSE");//End without exiting
}
void swap(int *a, int *b){
int temp;
temp = *a;
*a = *b;
*b = temp;
}
Quick sort:
Quick sort algorithm is an improved algorithm based on bubble sort,
The basic idea of its implementation is to divide the whole unordered table into two independent parts through one-time sorting, in which the data in one part is smaller than the data contained in the other part, and then continue to use this method to perform the same operation on the two parts respectively,
Until each small part can no longer be divided, the whole sequence becomes an ordered sequence.

The specific implementation code of the operation process is:
#define _CRT_SECURE_NO_WARNINGS / / avoid scanf errors
#include <stdio.h>
#include <stdlib.h>
#define MAX 9
//Structure of a single record
typedef struct {
int key;
}SqNote;
//Structure of record table
typedef struct {
SqNote r[MAX];
int length;
}SqList;
//In this method, in the array of records stored, the position with subscript 0 is marked in time and space, and no records are placed. The records are stored in turn from the position with subscript 1
int Partition(SqList *L, int low, int high){
L->r[0] = L->r[low];
int pivotkey = L->r[low].key;
//Until the two pointers meet, the program ends
while (low<high) {
//The high pointer moves to the left until a record smaller than the pivotkey value is encountered, and the pointer stops moving
while (low<high && L->r[high].key >= pivotkey) {
high--;
}
//Directly move the record that is less than the fulcrum pointed by high to the position of the low pointer.
L->r[low] = L->r[high];
//The low pointer moves to the right until a record larger than the pivotkey value is encountered, and the pointer stops moving
while (low<high && L->r[low].key <= pivotkey) {
low++;
}
//Directly move the record pointed to by low that is larger than the fulcrum to the position of the high pointer
L->r[high] = L->r[low];
}
//Add the fulcrum to the exact location
L->r[low] = L->r[0];
return low;
}
void QSort(SqList *L, int low, int high){
if (low<high) {
//Find the location of the fulcrum
int pivotloc = Partition(L, low, high);
//Sort the sub table on the left side of the fulcrum
QSort(L, low, pivotloc - 1);
//Sort the sub table on the right side of the fulcrum
QSort(L, pivotloc + 1, high);
}
}
void QuickSort(SqList *L){
QSort(L, 1, L->length);
}
void main() {
SqList * L = (SqList*)malloc(sizeof(SqList));
L->length = 8;
L->r[1].key = 49;
L->r[2].key = 38;
L->r[3].key = 65;
L->r[4].key = 97;
L->r[5].key = 76;
L->r[6].key = 13;
L->r[7].key = 27;
L->r[8].key = 49;
QuickSort(L);
for (int i = 1; i <= L->length; i++) {
printf("%d ", L->r[i].key);
}
system("PAUSE");//End without exiting
}
Click more sorting algorithms: http://data.biancheng.net/sort/ (insert sort algorithm, quick sort algorithm, select sort algorithm, merge sort and cardinal sort, etc.)
3. Binary search algorithm
Two point search is half search,
The basic idea is: first, select the record in the middle of the table and compare its keyword with the given keyword key. If it is equal, the search is successful;
If the key value is greater than the keyword value, the element to be found must be in the right sub table, and continue to search the right sub table in half;
If the key value is smaller than the key value, the element to be found must be in the left sub table. Continue to search the left sub table in half.
This is repeated until the search succeeds or fails (or the search range is 0).
For example:
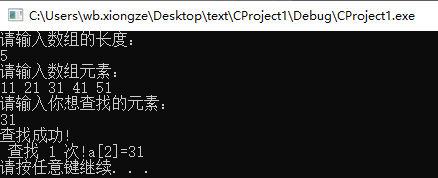
The user is required to enter the array length, that is, the data length of the ordered table, and enter the array elements and search keywords.
The program outputs whether the search is successful or not, and the position of the keyword in the array when it is successful.
For example, find the element with keyword 89 in the ordered tables 11, 13, 18, 28, 39, 56, 69, 89, 98 and 122.
#define _CRT_SECURE_NO_WARNINGS / / avoid scanf errors
#include <stdio.h>
int binary_search(int key, int a[], int n) //Custom function binary_search()
{
int low, high, mid, count = 0, count1 = 0;
low = 0;
high = n - 1;
while (low<high) //Execute loop body statement when the search range is not 0
{
count++; //count record search times
mid = (low + high) / 2; //Find the middle position
if (key<a[mid]) //When key is less than the middle value
high = mid - 1; //Determine the left sub table range
else if (key>a[mid]) //When the key is greater than the intermediate value
low = mid + 1; //Determine the right sub table range
else if (key == a[mid]) //When the key is equal to the intermediate value, the search is successful
{
printf("Search succeeded!\n lookup %d second!a[%d]=%d", count, mid, key); //Output the number of searches and the position of the searched element in the array
count1++; //count1 records the number of successful searches
break;
}
}
if (count1 == 0) //Determine whether the search failed
printf("Search failed!"); //Search failed, output no found
return 0;
}
int main()
{
int i, key, a[100], n;
printf("Please enter the length of the array:\n");
scanf("%d", &n); //Enter the number of array elements
printf("Please enter an array element:\n");
for (i = 0; i<n; i++)
scanf("%d", &a[i]); //Enter an ordered sequence of numbers into array a
printf("Please enter the element you want to find:\n");
scanf("%d", &key); //Enter the keyword you want ^ to find
binary_search(key, a, n); //Call custom function
printf("\n");
system("PAUSE");//Do not exit after completion;
}
4. Search algorithm
Search algorithm is a method that uses the high performance of computer to purposefully enumerate some or all possible situations in the solution space of a problem, so as to find the solution of the problem.
At present, there are generally enumeration algorithm, depth first search, breadth first search, A * algorithm, backtracking algorithm, Monte Carlo tree search, hash function and other algorithms.
In the large-scale experimental environment, the search scale is usually reduced according to the conditions before the search;
Pruning according to the constraints of the problem; Using the intermediate solution in the search process to avoid repeated calculation, these methods are optimized.
Here is the depth first search, interested can baidu query more search algorithms.
There are many contents. You can query the usage you are interested in Baidu: you can also click depth first search to see more.
Depth first search
- Depth first traversal first accesses the starting point v and marks it as visited; Then start from V and search each adjacent point w of V in turn. If W has not been accessed, continue the depth first traversal with w as the new starting point until all vertices connected with the path of the source point v in the graph have been accessed.
- If there are still unreachable vertices in the graph, select another unreachable vertex as a new source point and repeat the above process until all vertices in the graph have been accessed.
Depth search and breadth search are similar, and ultimately all the child nodes of a node should be extended
The difference is that in the process of expanding the node, the deep search expands one of the adjacent nodes of the E-node, and continues to expand it as a new E-node. The current E-node is still a live node. After searching its child nodes, go back to the node to expand its other unsearch adjacent nodes.
Breadth search extends all adjacent nodes of E-node, and E-node becomes a dead node.
5. Hash algorithm
1. What is hash
Hash, generally translated as hash, hash, or transliterated as hash, is a typical algorithm that uses space for time. The input of any length (also known as pre mapping pre image) is transformed into a fixed length output through the hash algorithm, and the output is the hash value.
If there is a student information form:
The student number is: age + College number + class number + sequence number [e.g. 19 (age) + 002 (College 2) + 01 (Class 1) + 17 (No. 17) - à 190020117], which is similar to such information,
When we need to find the student with the student number [190020117], when hash is not applicable, we usually use a sequential traversal method to query the large class in the data, and then query the subclass to get it,
This method is obviously not fast enough and takes about O(n), which is obviously not good for large data scale,
The hash method is to compress [190020117] into a short data according to certain rules (for example, age is not too old or too young), such as:
[192117]) and directly apply this data to the memory address. At that time, we only need to compress [190020117] once and access the address of [192117], and this compression method (function) can be called hash function.
In general, the following should be considered for hash functions:
The time required to calculate the hash address (that is, the hash function itself should not be too complex)
Length of keyword
Table length (not too long or too short to avoid memory waste and computing power consumption)
Whether the keyword distribution is uniform and whether there is a rule to follow
The hash function is designed to minimize the conflict when the above conditions are met
2. Hash and hash table
After understanding the thinking of hash, we need to understand what is a hash table. As the name suggests, a hash table is a table converted by a hash function,
By accessing the hash table, we can quickly query the hash table to obtain the required data. The core of building the hash table is to consider the conflict processing of the hash function (that is, after data compression, there may be multiple data with the same address, and the conflicting data needs to be stored separately by algorithm).
There are many methods to deal with conflicts. The simplest one is the + 1 method, that is, the number of addresses is directly + 1. When both data need to be stored in [2019], one of them can be considered to be stored in [2020]
In addition, there are open addressing method, chain address sending, public overflow method, re hashing method, prime number method and so on. Each method has different effects on different data characteristics.
3. Hash thinking
Hash algorithm is a generalized algorithm, which can also be regarded as an idea. Using hash algorithm can improve the utilization of storage space, improve the query efficiency of data, and make digital signature to ensure the security of data transmission.
Therefore, Hash algorithm is widely used in Internet applications.
For example, using the idea of hash, arbitrarily query all prime numbers within 1000 under the complexity of O(1) (it is not the complexity of O(1) when creating whether it is a prime number),
Note that this example is just a demonstration of thinking, and there can be a better way to use space in the face of this demand (this writing method is a waste of space, for understanding only).
Examples are as follows:
[telephone chat madman]
Given the call records of a large number of mobile phone users, find out the chat madman with the most calls.
Input format:
The input first gives a positive integer N (≤ 10 ~ 5), which is the number of call records. Then N lines, each line gives a call record. For simplicity, only the 11 digit mobile phone numbers of the caller and the receiver are listed here, separated by spaces.
Output format:
Give the mobile phone number of the chat madman and the number of calls in one line, separated by spaces. If such a person is not unique, the minimum number of madmen and the number of calls will be output, and the number of parallel madmen will be given.
Input sample:
4 13005711862 13588625832 13505711862 13088625832 13588625832 18087925832 15005713862 13588625832
Output example:
13588625832 3
#define _CRT_SECURE_NO_WARNINGS / / avoid scanf errors
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <stdlib.h>
#include <ctype.h>
#define MAX 400000 / * * define the maximum array size * * / / / (it's useless, but it's best to open it as large as possible, but not too large, not beyond the buildable range of the system)
typedef struct Node *Hash; /**The new journey begins again. This time, we are going to use arrays to hash and two-way square to deal with conflicts**/
struct Node{
char phone[15];
int num;
};
int maxInt(int x, int y)
{
if (x>y) return x;
else return y;
}
char* minstr(char *x, char *y)
{
if (strcmp(x, y)>0) return y;
else return x;
}
int nextprime(const int n)
{
int p = (n % 2 == 1) ? n + 2 : n + 1; /**Find an odd number greater than N first**/
int i;
while (p<MAX)
{
for (i = (int)sqrt(p); i >= 2; i--) /**Then judge whether it is a prime number**/
if (p%i == 0) break;
if (i<2) return p; /**Yes, then return this number**/
else p += 2;/**No, then the next odd number**/
}
}
int deal(char *s, int p) /**Then map the string into a subscript (there are many ways to map, just guess a reliable one)**/
{
int index = (atoi(s + 2)) % p;
return index;
}
int insert(Hash h, int pos, char *s, int p, int Max) /**Hash search insert implementation, namely hash array, array location, ID number, the largest array size, MAX saw the code finally understand **/
{
int i, posb = pos; /**Backup pos value to facilitate two-way square search**/
for (i = 1;; i++)
{
if (strcmp(h[pos].phone, "") == 0) /**If the value of pos is null, insert it directly**/
{
strcpy(h[pos].phone, s);
h[pos].num++;
Max = max(Max, h[pos].num);
break;
}
else
{
if (strcmp(h[pos].phone, s) == 0) /**If you are not empty, check if the ID number is waiting.*/
{
h[pos].num++;
Max = maxInt(Max, h[pos].num);
break;
}
else
{ //Original p%2==1
if (i % 2 == 1) pos = (posb + (i*i)) % p; /**If it is not equal, find the next position, find it backward and forward respectively, and cycle like this**/
else
{ //Original i*i
pos = posb - ((i - 1)*(i - 1));
while (pos<0)
pos += p;
}
}
}
}
return Max;
}
void initial(Hash h, int p) /**Initialize the hash array**/
{
int i;
for (i = 0; i<p; i++)
{
h[i].phone[0] = '\0';
h[i].num = 0;
}
}
int main(){
int Max = 0;
int n; /**Total N, and then start looking for the minimum prime greater than n**/
scanf("%d", &n); /**Input \ n into the output to avoid strange things in the following input**/
int p = nextprime(2 * n); /**Suddenly remembered that each time I entered two phone numbers, so the maximum number of phone numbers is 2*n**/
Hash h = (Hash)malloc(p*sizeof(struct Node));/**Create hash array**/
initial(h, p);
char phone[15];
char phone1[15];
while (n--)
{
scanf("%s %s", phone, phone1);
Max = insert(h, deal(phone, p), phone, p, Max);
Max = insert(h, deal(phone1, p), phone1, p, Max);
}
int i, num = 0;
char *Minstr = NULL;
for (i = 0; i<p; i++)
{
if (h[i].num == Max)
{
if (Minstr == NULL) Minstr = h[i].phone;
else Minstr = minstr(Minstr, h[i].phone);
num++;
}
}
printf("%s %d", Minstr, Max);
if (num>1) printf(" %d", num);
system("PAUSE");//End without exiting
}
6. Greedy algorithm
Greedy algorithm (also known as greedy algorithm) means that when solving a problem, it always makes the best choice at present.
In other words, without considering the overall optimization, what he makes is only the local optimal solution in a sense.
Greedy algorithm can not get the global optimal solution for all problems, but it can produce the global optimal solution or the approximate solution of the global optimal solution for a wide range of problems.
The basic idea of greedy algorithm is to start from an initial solution of the problem step by step. According to an optimization measure, each step should ensure that the local optimal solution can be obtained. Only one data is considered in each step, and its selection should meet the conditions of local optimization until all data are enumerated.
The idea of greedy algorithm is as follows:
Establish a mathematical model to describe the problem;
The problem is divided into several subproblems;
Each subproblem is solved to obtain the local optimal solution of the subproblem;
The local optimal solution of the subproblem is synthesized into a solution of the original problem.
Different from dynamic programming, greedy algorithm obtains a local optimal solution (that is, it may not be the most ideal), while dynamic programming algorithm obtains a global optimal solution (that is, it must be the most ideal as a whole),
An interesting thing is that the 01 knapsack problem in dynamic programming is a typical greedy algorithm problem.
The following example: greedy algorithm monetary statistics problem
#define _CRT_SECURE_NO_WARNINGS / / avoid scanf errors
#include <stdio.h>
#include <malloc.h>
void main()
{
int i, j, m, n, *ns = NULL, *cn = NULL, sum = 0;
printf("Please enter the total amount m And types of change n: "), scanf("%d", &m), scanf("%d", &n);
printf("Please enter separately%d Denomination of change:\n", n);
if (!(ns = (int *)malloc(sizeof(int)*n))) return 1;
if (!(cn = (int *)malloc(sizeof(int)*n))) return 1;
for (i = 0; i<n; i++) scanf("%d", &ns[i]);
//------------Considering that the order of entering denominations is uncertain, the denominations shall be arranged in descending order first (if they are entered in descending order, this segment can be deleted)
for (i = 0; i<n; i++)
for (j = i + 1; j<n; j++)
if (ns[j]>ns[i]) ns[j] ^= ns[i], ns[i] ^= ns[j], ns[j] ^= ns[i];
for (i = 0; i<n; i++)//Greedy algorithm, starting from the maximum denomination
if (m >= ns[i])
cn[i] = m / ns[i], m = m%ns[i], sum += cn[i], printf("%d element%d Zhang ", ns[i], cn[i]);
printf("\n Minimum use of change%d Zhang\n", sum);
system("PAUSE");//End without exiting
}

7. Divide and conquer algorithm
The basic idea of divide and conquer algorithm is to decompose a problem with scale N into K smaller subproblems, which are independent of each other and have the same properties as the original problem.
If the solution of the subproblem is obtained, the solution of the original problem can be obtained. That is, a sub objective completion program algorithm. Simple problems can be completed by dichotomy.
Find the n-th power of x
Complexity is O(lgn)
#define _CRT_SECURE_NO_WARNINGS / / avoid scanf errors
#include "stdio.h"
#include "stdlib.h"
int power(int x, int n)
{
int result;
if (n == 1)
return x;
if (n % 2 == 0)
result = power(x, n / 2) * power(x, n / 2);
else
result = power(x, (n + 1) / 2) * power(x, (n - 1) / 2);
return result;
}
void main()
{
int x = 5;
int n = 3;
printf("power(%d,%d) = %d \n", x, n, power(x, n));
system("PAUSE");//End without exiting
}
Merge sort
The time complexity is O(NlogN)O(Nlog N), and the spatial replication degree is O(N)O(N) (the biggest defect of merge sorting)
Merge Sort completely follows the above three steps of divide and Conquer:
- Decomposition: decompose the sequence of n elements to be sorted into two subsequences with n/2 elements;
- Solution: use merge sort to recursively sort two subsequences respectively;
- Merge: merge two sorted subsequences to produce the solution of the original problem.
#define _CRT_SECURE_NO_WARNINGS / / avoid scanf errors
#include "stdio.h"
#include "stdlib.h"
#include "assert.h"
#include "string.h"
void print_arr(int *arr, int len)
{
int i = 0;
for (i = 0; i < len; i++)
printf("%d ", arr[i]);
printf("\n");
}
void merge(int *arr, int low, int mid, int hight, int *tmp)
{
assert(arr && low >= 0 && low <= mid && mid <= hight);
int i = low;
int j = mid + 1;
int index = 0;
while (i <= mid && j <= hight)
{
if (arr[i] <= arr[j])
tmp[index++] = arr[i++];
else
tmp[index++] = arr[j++];
}
while (i <= mid) //Copy the remaining left half
tmp[index++] = arr[i++];
while (j <= hight) //Copy the remaining right half
tmp[index++] = arr[j++];
memcpy((void *)(arr + low), (void *)tmp, (hight - low + 1) * sizeof(int));
}
void mergesort(int *arr, int low, int hight, int *tmp)
{
assert(arr && low >= 0);
int mid;
if (low < hight)
{
mid = (hight + low) >> 1;
mergesort(arr, low, mid, tmp);
mergesort(arr, mid + 1, hight, tmp);
merge(arr, low, mid, hight, tmp);
}
}
//Allocate memory only once to avoid memory operation overhead
void mergesort_drive(int *arr, int len)
{
int *tmp = (int *)malloc(len * sizeof(int));
if (!tmp)
{
printf("out of memory\n");
exit(0);
}
mergesort(arr, 0, len - 1, tmp);
free(tmp);
}
void main()
{
int data[10] = { 8, 7, 2, 6, 9, 10, 3, 4, 5, 1 };
int len = sizeof(data) / sizeof(data[0]);
mergesort_drive(data, len);
print_arr(data, len);
system("PAUSE");//End without exiting
}
There are more examples to Baidu, not one by one here.
8. Backtracking algorithm
Backtracking algorithm, also known as "heuristics". When solving problems, every step is taken with a try attitude. If you find that the current choice is not the best, or if you go on like this, you will certainly not achieve your goal, immediately go back and choose again.
This method of going back and going again if it doesn't work is the backtracking algorithm.
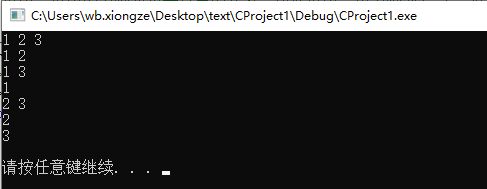
For example, the backtracking algorithm can be used to solve the problem of enumerating all subsets in the set {1,2,3}.
Starting with the first element of the collection, there are two choices for each element: take or discard. After determining the trade-off of one element, proceed to the next element until the last element of the collection.
Each of these operations can be regarded as an attempt, and each attempt can produce a result. The results obtained are all subsets of the set.
#define _CRT_SECURE_NO_WARNINGS / / avoid scanf errors
#include <stdio.h>
//Set an array. The subscript of the array represents the elements in the collection, so the array only uses the space with subscripts 1, 2 and 3
int set[5];
//i represents the array subscript, and n represents the largest element value in the collection
void PowerSet(int i, int n){
//When I > N, it indicates that all elements in the set have been selected and begin to judge
if (i>n) {
for (int j = 1; j <= n; j++) {
//If 1 is stored in the tree group, it means that the element, that is, the corresponding array subscript, is selected when trying. Therefore, it can be output
if (set[j] == 1) {
printf("%d ", j);
}
}
printf("\n");
}
else{
//If this element is selected, the corresponding array cell is assigned a value of 1; Conversely, the value is assigned to 0. Then continue to explore downward
set[i] = 1; PowerSet(i + 1, n);
set[i] = 0; PowerSet(i + 1, n);
}
}
void main() {
int n = 3;
for (int i = 0; i<5; i++) {
set[i] = 0;
}
PowerSet(1, n);
system("PAUSE");//End without exiting
}
Many people think that backtracking is the same as recursion, but it's not. Recursion can be seen in the backtracking method, but there are differences between the two.
The backtracking method starts from the problem itself and looks for all possible situations. Similar to the idea of exhaustive method, the difference is that the exhaustive method lists all the situations and then screens them again, while the retrospective method stops all subsequent work and returns to the previous step for a new attempt if it finds that the current situation is impossible in the listing process.
Recursion starts from the result of the problem, such as finding n!, Want to know n! You need to know n*(n-1)! And want to know (n-1)! As a result, you need to know in advance (n-1)*(n-2)!. In this way, constantly asking yourself questions and constantly calling your thoughts is recursion.
The process of using backtracking method to solve problems is actually the process of establishing a "state tree".
For example, in solving the problem of enumerating all subsets of the set {1,2,3}, there are two states for each element, take or reject, so the constructed state tree is:
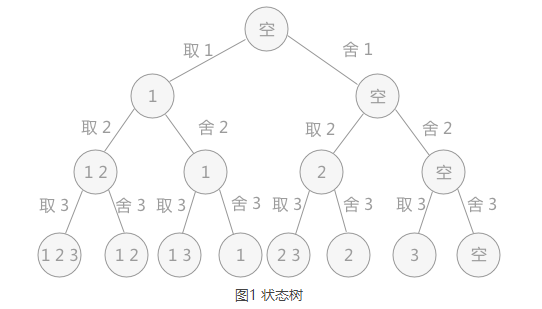
The solution process of backtracking algorithm is essentially the process of traversing the "state tree" in sequence. Every leaf node in the tree may be the answer to the question. The state tree in Figure 1 is a full binary tree, and all the leaf nodes obtained are the solutions of the problem.
In some cases, the state trees created in the process of backtracking algorithm solving the problem are not all full binary trees, because it is sometimes found in the process of trial,
There is no point in moving on, so I will give up this dead end and go back to the previous step. The embodiment in the tree is that the last layer of the tree is not full, that is, it is not a full binary tree. You need to judge which leaf nodes represent the correct result.
9. Dynamic programming (DP) algorithm
Dynamic programming process: every decision depends on the current state, that is, the generation of the next state depends on the current state. A decision sequence is generated in a changing state. The solution process of this multi-stage optimization problem is a dynamic rule process.
Basic ideas and principles
Similar to the divide and conquer principle, the problem to be solved is divided into several sub problems (stages) for solution, and each sub problem (stage) is solved in sequence. The former sub problem (stage) provides useful information for the solution of the latter sub problem (stage).
Through the solution of each sub problem (stage), the solution of the initial problem is obtained. Generally, problems that can be solved by dynamic programming can also be solved by recursion.
Most problems solved by dynamic programming have the characteristics of overlapping subproblems. In order to reduce repeated calculation, each subproblem is solved only once, and the solutions of different subproblems (stages) are saved in the array.
Difference from divide and rule:
Several sub problems (stages) obtained by divide and rule are generally independent of each other, and there is no order requirement between each sub problem (stage). In dynamic programming, the solution of each subproblem (stage) has sequential requirements and has overlapping subproblems (stages). The solution of the latter subproblem (stage) depends on the solution of the previous subproblem (stage).
Difference from recursion:
It is not different from recursive solution. It is divided into sub problems (stages). The latter sub problem (stage) depends on the former sub problem (stage), but recursion needs to solve the same sub problem (stage) repeatedly. Compared with dynamic programming, it has done a lot of repetitive work.
Applicable problem solving
The problems solved by dynamic programming generally have the following properties:
- Optimization principle: the solution problem contains the optimal substructure, that is, the optimal solution of the next sub problem (stage) can be derived from the optimal solution of the previous sub problem (stage), and the optimal solution of the initial problem can be obtained step by step.
- No aftereffect: the process after a certain state will not affect the previous state, but only related to the current state.
- Overlapping subproblems: subproblems (stages) are not independent, and the solution of one subproblem (stage) is used in the next subproblem (stage). (not a necessary condition, but dynamic programming is better than the basis of other methods)
For example, Fibonacci sequence is a simple example.
definition:
Fab(n)= Fab(n-1)+Fab(n-2) Fab(1)=Fab(2)=1;
Implementation 1:
static int GetFab(int n)
{
if (n == 1) return 1;
if (n == 2) return 1;
return GetFab(n - 1) + GetFab(n - 2);
}
If we ask Fab(5). Then we need to find Fab (4) + Fab (3).
Fab(4)=Fab(3)+Fab(2)... Obviously. Fab (3) is calculated twice by the computer without distinction. And as the number increases, the amount of calculation increases exponentially.
If we use an array, record the value of Fab. When Fab (n)= Null.
Direct read. Then, we can control the time complexity within n.
Implementation 2:
static int[] fab = new int[6];
static int GetFabDynamic(int n)
{
if (n == 1) return fab[1] = 1;
if (n == 2) return fab[2] = 1;
if (fab[n] != 0)//If it exists, return directly.
{
return fab[n];
}
else //If it does not exist, it enters recursion and records the obtained value.
{
return fab[n] = GetFabDynamic(n - 1) + GetFabDynamic(n - 2);
}
}
This is the memo mode of dynamic programming algorithm. Just modify the original recursion slightly.
The following is the solution of the 0-1 knapsack problem.
You can compare it. (a weight limited w backpack has many items. sizes[n] saves their weight. values[n] saves their value. Find the maximum value that the backpack can hold without being overweight)
static int[] size = new int[] { 3, 4, 7, 8, 9 };// Each of the 5 items is 3, 4, 7, 8 and 9 in size and is an integral 0-1 knapsack problem
static int[] values = new int[] { 4, 5, 10, 11, 13 }; 5 The value of each item is 4, 5, 10, 11, 13
static int capacity = 16;
static int[,] dp = new int[6, capacity + 1];
static int knapsack(int n, int w)
{
if (w < 0) return -10000;
if (n == 0) return 0;
if (dp[n, w] != 0)
{
return dp[n, w];
}
else
{
return dp[n, w] = Math.Max(knapsack(n - 1, w), knapsack(n - 1, w - size[n - 1]) + values[n - 1]);
/*
* knapsack(n,w) It refers to the maximum value of the first N items under W residual capacity.
* This formula means that for an object,
* 1,If you choose to put it in, the current value = the maximum value of the previous n-1 items under the vacancy w - size(n) (because the vacancy needs to be reserved, the vacancy also implies the value).
* Plus the value of this item. Equal to knapsack(n - 1, w - size[n - 1]) + values[n - 1]
* 2, If we choose not to put it in, then in the case of n-1 items, the vacancy is still there, and the current value = the maximum value of the previous n-1 items in the vacancy w.
* Equal to knapsack(n - 1, w)
* Note: with the calculus, the value in a certain case will not remain the same.
* At this point, we make a decision: is it more valuable when loading or not? We choose the one with the larger value in the above two cases. And put it on record.
* Finally dp[N,M] is the value we require.
*/ }
}
10. String matching algorithm
Formal definition of string matching problem:
- Text is an array T[1... N] with length n;
- Pattern is an array P[1... M] with length m and m ≤ n;
- The elements in T and P belong to a finite alphabet Σ Table;
- If 0 ≤ s ≤ n-m, and T[s+1... s+m] = P[1... M], that is, for 1 ≤ j ≤ m, T[s+j] = P[j], then mode P
If it appears in text T and the displacement is s, s is said to be a Valid Shift.
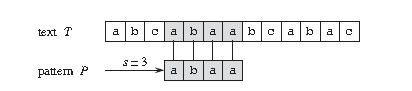
For example, in the above figure, the goal is to find all occurrences of pattern P = abaa in the text T = abcabaabcabac.
This mode occurs only once in this text, i.e. at the position shift s = 3, the displacement S = 3 is the effective displacement.
Algorithms to solve string matching include:
- Naive Algorithm
- Rabin Karp algorithm
- Finite Automation
- Knuth Morris Pratt algorithm (KMP Algorithm), Boyer Moore algorithm, Simon
Algorithm, Colussi algorithm
Galil Giancarlo algorithm, Apostolico crochemore algorithm, horpool algorithm, Sunday algorithm, etc.).
String Matching algorithm is usually divided into two steps: Preprocessing and Matching. Therefore, the total running time of the algorithm is the sum of Preprocessing and Matching time.

The figure above describes the preprocessing and matching time of common string matching algorithms.
There are many designs here. You can learn the specified algorithm according to your needs.
String matching algorithm,KMP algorithm for string matching in C language
reference
Sorting algorithm: http://data.biancheng.net/sort/
C language binary search algorithm, half search algorithm: http://c.biancheng.net/view/536.html
Greedy algorithm: https://blog.csdn.net/yongh701/article/details/49256321
String matching algorithm: https://www.cnblogs.com/gaochundong/p/string_matching.html
C language implements string matching KMP algorithm: https://www.jb51.net/article/54123.htm
Welcome to subscribe to WeChat public official account.
Author: Xiong Ze - pain and joy in learning
Official account: Bear's saying
QQ group: 711838388
Source 1: https://www.cnblogs.com/xiongze520/p/15816597.html
Source 2: https://blog.csdn.net/qq_35267585/article/details/122573608
You can reprint and excerpt at will, but please indicate the author and the link to the original text in the article.
