Advantages of binary tree:
It can be accessed very efficiently on the binary tree.
Binary tree is very suitable for interval operation. A subtree in a binary tree can be regarded as a sub interval of the whole tree. It is very fast to find the interval maximum, interval sum, interval flip, interval merge, interval split, etc.
Binary tree is very simple to search and process with BFS and DFS. Binary tree can be searched layer by layer, which is BFS. Any child node of a binary tree is a binary tree with it as its root. This is a recursive structure. It is a perfect match to traverse a binary tree with DFS.

Storage (Implementation) of binary tree

For a node of a binary tree, we usually store the value of the node and the left and right child nodes.

struct Node{              //Static binary tree
   char value;
   int lson, rson;        //For left and right children, lson is abbreviated as ls or l
}tree[N];                 //When coding, the tree is abbreviated as t

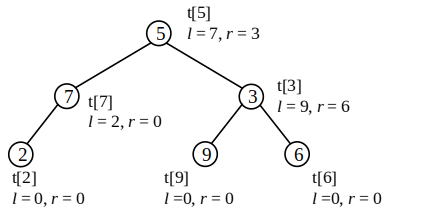
The following figure illustrates a binary tree, whose root is tree[5]tree[5].

tree[0] is generally not used in coding, because 00 is used to represent empty nodes. For example, leaf node tree[2] has no child nodes, so its child nodes are assigned lson = rson = 0.

In particular, we can use arrays to represent complete binary trees, which is very convenient to access. At this time, even lson and rson are not required. A complete binary tree with a total number of nodes k, with point 1 as the root node, has the following properties: for a node with i > 1, its parent node is i / 2.

If node i has children, then its left child is 2 × i. The right child is 2 × i+1.
If 2 × i> K, then I have no children; If 2 × I + 1 > k, then I has no right child.

Width first traversal (bfs)

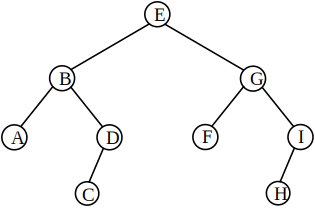
Width first traversal is to traverse the binary tree layer by layer from top to bottom according to the hierarchy of the tree. For example, in the following figure, you need to access in the order of "HEBGADFICH". It is most appropriate to search BFS with width first, which will be explained in detail in the BFS topic later.

Depth first traversal

Using depth first search DFS to traverse the binary tree, the code is extremely simple.
Access the binary tree in the order of deep search, and combine the parent node, left son and right son. There are three access sequences: first (parent) order traversal, middle (parent) order traversal and last (parent) order traversal. Here, the left son is in front of the right son by default.
First order

void preorder (node *root){ 
     cout << root ->value;        //output
     preorder (root -> lson);      //Recursive left subtree
     preorder (root -> rson);      //Recursive right subtree
}

Middle order

void inorder (node *root){ 
     inorder (root -> lson);      //Recursive left subtree
     cout << root ->value;         //output
     inorder (root -> rson);      //Recursive right subtree
}

Post order

void postorder (node *root){ 
     postorder (root -> lson);      //Recursive left subtree
     postorder (root -> rson);      //Recursive right subtree
     cout << root ->value;        //output
}

Title: FBI tree

#include <bits/stdc++.h>
using namespace std;
char s[2000],tree[280000]; //Tree [] full binary tree

void build_FBI(int k,int left,int right){
        if(left==right){      //Reach leaf node
        if(s[right]=='1') tree[k]='I';
        else tree[k]='B';
        return;
        }
        int mid=(left+right)/2;      //Split in half
        build_FBI(2*k,left,mid);     //Recursive left half
        build_FBI(2*k+1,mid+1,right); //Recursive right half

        if(tree[2*k]=='B' && tree[2*k+1]=='B') //Both sons are B
        tree[k]='B';
        else if(tree[2*k]=='I'&&tree[2*k+1]=='I') //Both left and right sons are I
        tree[k]='I';
        else tree[k]='F';
}
void postorder (int v){   //Postorder traversal
        if(tree[2*v])         postorder (2*v);
        if(tree[2*v+1])         postorder (2*v+1);
        printf("%c",tree[v]);
}
int main(){
        int n;        scanf("%d",&n);
        scanf("%s",s+1);
        build_FBI(1,1,strlen(s+1));
        postorder(1);
}

Title: weight of complete binary tree

Given a complete binary tree with N nodes, each node in the tree has a weight, which is A1, A2 and an from top to bottom and left to right. Now Xiao Ming wants to add the weights of nodes with the same depth. He wants to know which depth has the largest sum of node weights? If the weight sum of multiple depths is the largest, please output the smallest depth.

#include<bits/stdc++.h>
using namespace std;
int a[101000];
int p(int x){
    int t=1;
    while(x--) t*=2;
     return t;
}
int main(){
    int n,t=1,i=2,j=2;
    scanf("%d %d",&n,&a[1]);
    long long maxx=a[1];
    for(int i=2;i<=n;i++) scanf("%d",&a[i]);
    while(i<=n){
        long long k=0;
        for(;i<p(j)&&i<=n;i++) k+=a[i];
        if(k>maxx)  
                maxx=k,t=j;
        j++;
  }
   cout<<t<<endl;
   return 0;
}