[preface]
Recently, I reviewed the exercises related to binary tree and shared some basic exercises according to the courseware
Tree is the top priority in data structure, especially the basic problems of various binary trees. I hope to deeply understand binary trees by summarizing the basic problems of binary trees.

[introduction to binary tree concept]
Degree of node
: the number of subtrees in a node is called the degree of the node;
Degree of tree
: the maximum degree of all nodes in a tree is called the degree of the tree;
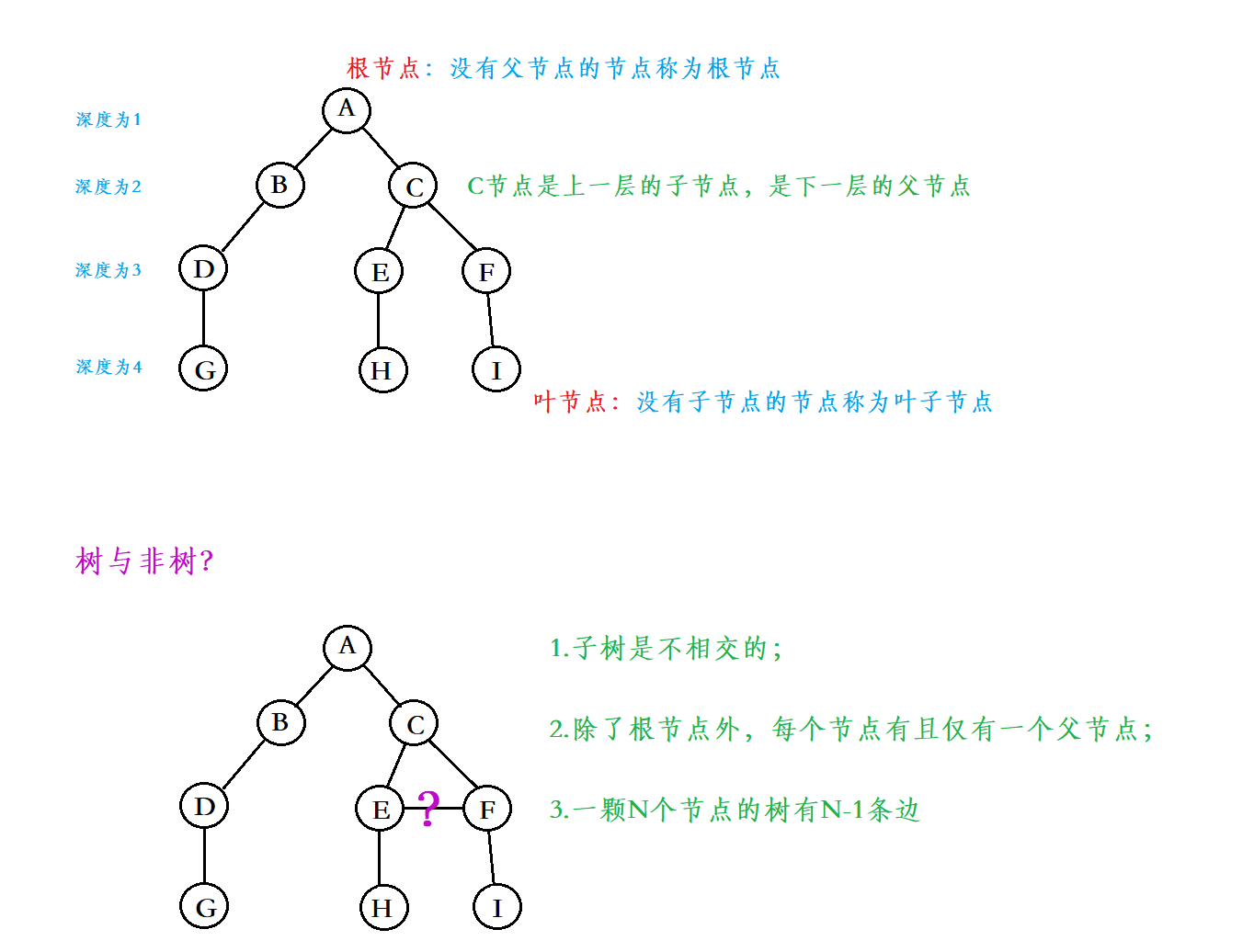
Leaf node or terminal node
: degree
0
The node of is called leaf node;
Parent node or parent node
: if a node contains child nodes, the node is called the parent node of its child nodes;
Child node or child node
: the root node of the subtree contained in a node is called the child node of the node;
Root node
: nodes in a tree without parent nodes;
Hierarchy of nodes
: from the definition of the root, the root is the second
Layer 1, the child node of the root is layer 2, and so on
The height or depth of a tree
: the maximum level of nodes in the tree;
[properties of binary tree]
1.
If the number of layers of the specified root node is 1, there are at most (2 ^ (i - 1)) (i > 0) nodes on layer i of a non empty binary tree
2. If it is specified that the depth of a binary tree with only root nodes is 1, the maximum number of nodes of a binary tree with depth K is 2 ^ k-1 (k > = 0)
3. For any binary tree, if the number of leaf nodes is n0 and the number of non leaf nodes with degree 2 is n2, then n0 = n2 + 1
4. The depth k of a complete binary tree with n nodes is rounded on log(n+1)
[basic knowledge of binary tree]
[get the number of nodes in the tree]
int size(Node root){//Get the number of nodes in the tree
int count = 0;
if(root == null){
return 0;
}
count ++;
size( root.left);
size( root.right);
return count;
}
[obtain the number of leaf nodes]
static leafcount = 0;
void getLeafNodeCount(TreeNode root){
if(root == null) return ;
if(root.left == null && root.right == null){
leafcount ++;
}
getLeafNodeCount( root.left);
getLeafNodeCount( root.right);
}[/ / get the number of layer K nodes]
int getKLevelNodeCount(Node root, int k){
if(root == null || k < 0) return -1;
if(k == 1){
return 1;
}
return getKLevelNodeCount(root.left,k-1) + getKLevelNodeCount(root.right, k-1);
}
[get the height of binary tree]
int getHeight(Node root){
if(root == null) return 0;//
int high1 = getHeight( root.left);//Calculate the height on the left side of the recursive tree
int high2 = getHeight(root.right);//Calculate the height on the right side of the recursive tree
if(high1 > high2) {
return high1 + 1;//Add root node when returning
}else{
return high2 + 1;
}
[check whether the element with value exists]
TreeNode find(Node root, int val){//Check whether the value exists
if(root == null) return null;
if(root.val = val) return root;
TreeNode val1 = find( root.left, val)
if( val1!= null){
return val1
}
TreeNode val2 = find( root.right, val);
if(val2 != null){
return val2;
}
return null;
[judge whether a tree is a complete binary tree]
public boolean isBalanced(TreeNode root) {
return high(root) > 0;
}
public int high( TreeNode root1 ){
if(root1 == null ) return 1;
int high1 = high(root1.left );//Recursive left height of tree
int high2 = high(root1.right);// Right tree height
if(high1 == -1 || high2 == -1 || Math.abs(high1-high2 ) >1){//-1 means that if null is encountered, - 1 will be returned, indicating that there is no next node
return -1;
}else{
return Math.max(high1,high2)+1;
}
[check whether the two trees are the same]
public boolean isSameTree(TreeNode p, TreeNode q) {
if(p == null && q == null) return true;//When p and q are null at the same time, it indicates that the number of recursive end nodes is the same
if(p == null || q == null) return false;// Only one of the two is null, and the other is not finished. It returns false
if(p.val != q.val ) return false;//Compare the two values
return isSameTree(p.left, q.left) && isSameTree( p.right, q.right) ; //Both the left and right sides of the recursive tree
[subtree of another tree]
public boolean isSameTree(TreeNode p, TreeNode q) {//Determine whether it is the same as its subtree and the same as the previous tree
if(p == null && q == null) return true;
if(p == null || q == null) return false;
if(p.val != q.val ) return false;
return isSameTree(p.left, q.left) && isSameTree( p.right, q.right) ;
}
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
if(root == null || subRoot == root){
return false;
}
if(isSameTree(root,subRoot)){//Judge whether the root node is the same
return true;
}
if (isSubtree(root.left,subRoot )){//Is the left side of the recursive tree the same as the subtree
return true;
}
if(isSubtree(root.right,subRoot )){//Is the right side of the recursive tree the same as the subtree
return true;
}
return false;
}
[maximum depth of binary tree]
class Solution {
public int maxDepth(TreeNode root) {
if(root == null) return 0;
int high1 = maxDepth(root.left);//Recursively calculate the height on the left
int high2 = maxDepth(root.right);//Recursively calculate the height on the right
if(high1 > high2){The larger one plus the initial root node returns
return high1+1;
}else{
return high2+1;
}
}
}
[judge whether a binary tree is a balanced binary tree]
class Solution {
public boolean isBalanced(TreeNode root) {
return high(root) > 0;
}
public int high( TreeNode root1 ){
if(root1 == null ) return 1;
int high1 = high(root1.left );//Get left tree height
int high2 = high(root1.right);//Get right tree height
if(high1 == -1 || high2 == -1 || Math.abs(high1-high2 ) >1){
return -1;
}else{
return Math.max(high1,high2)+1;//
}
}
}
[symmetric binary tree]
class Solution {
public boolean isSymmetric(TreeNode root) {
return issame( root, root);
}
public boolean issame(TreeNode root1,TreeNode root2){//
if(root1 == null && root2 == null) return true; When both root nodes are null It indicates that it has reached the last node
if(root1 == null || root2 == null) return false;//Only one of the nodes reached null
return root1.val == root2.val && issame( root1.left, root2.right) && issame( root1.right, root2.left);// At the same time, because recursion is symmetrical, the left and right should be separated
}
}
[construction and traversal of binary tree]
import java.util.*;
class TreeNode{
public char val;
public TreeNode left;
public TreeNode right;
public TreeNode (char val){
this.val = val;
}
}
public class Main{
public static int i = 0;
public static TreeNode createTree(String str) {
TreeNode root = null;
if(str.charAt(i) != '#') {
root = new TreeNode(str.charAt(i));
i++;
root.left = createTree(str);
root.right = createTree(str);
}else {
i++;
}
return root;
}
public static void inorder(TreeNode root) {
if(root == null) return ;
inorder(root.left);
System.out.print(root.val+" ");
inorder(root.right);
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
while (in.hasNextLine()) {
String str = in.nextLine();
TreeNode root = createTree(str);
inorder(root);
}
}
}
[hierarchical traversal of binary tree]
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> ret = new ArrayList<>();//Define a linked list for storage
Queue<TreeNode> myqueue = new LinkedList<>();//Store elements in the stack
if(root == null) return ret;
myqueue.offer(root);//Put the root node on the stack
while(!myqueue.isEmpty()){
List<Integer> list = new LinkedList<>();
int size = myqueue.size();//Calculate the number of elements in the stack at this time
while(size != 0){
TreeNode cur = myqueue.poll();
list.add(cur.val);Put the top element in the stack into the linked list
if(cur.left != null){There are two cases
myqueue.offer(cur.left);
}
if(cur.right != null){
myqueue.offer(cur.right);
}
size--;
}
ret.add(list);
}
return ret;
}
}
[given a binary tree, find the nearest common ancestor of two specified nodes in the tree]
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null) return null;
Stack<TreeNode> stack1 = new Stack<>();
getPath( root, p, stack1);
Stack<TreeNode> stack2 = new Stack<>();
getPath( root,q, stack2);
int size1 = stack1.size();
int size2 = stack2.size();
if(size1 > size2){
int size = size1-size2;
while(size != 0){
stack1.pop();
size--;
}
while(!stack1.empty() && !stack2.empty()){
if(stack1.peek() == stack2.peek()){
return stack1.pop();
}else{
stack1.pop();
stack2.pop();
}
}
}else{
int size = size2-size1;
while(size != 0){
stack2.pop();
size--;
}
while(!stack1.empty() && !stack2.empty()){
if(stack1.peek() == stack2.peek()){
return stack1.pop();
}else{
stack1.pop();
stack2.pop();
}
[convert binary tree search tree into sorted two-way linked list]
/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
TreeNode pre = null;
public void inorder(TreeNode pCur) {
if(pCur == null) return ;
inorder(pCur.left);
pCur.left = pre;
if(pre != null){
pre.right = pCur;
}
pre = pCur;
inorder(pCur.right);
}
public TreeNode Convert(TreeNode pRootOfTree) {
if(pRootOfTree == null) return null;
inorder(pRootOfTree);
TreeNode head = pRootOfTree;
while(head.left != null){
head = head.left;
}
return head;
}
}
.
[implementation of non recursive traversal of binary tree preamble]
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> mylist = new ArrayList<Integer>();
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while( cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
// System.out.println(cur);
mylist.add(cur.val);
cur = cur.left;
}
TreeNode pre = stack.pop();
cur = pre.right;
}
return mylist;
}
}
.
[implementation of sequential non recursive traversal in binary tree]
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> mylist = new ArrayList<Integer>();//
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while( cur != null || !stack.isEmpty()){
while(cur != null){
stack.push(cur);Store the root node in the stack
cur = cur.left;//Define cur as the left tree
}
TreeNode pre = stack.pop();
mylist.add(pre.val);
cur = pre.right;take cur Defined as the right tree
}
return mylist;
}
}
[implementation of post order non recursive traversal of binary tree]
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> mylist = new ArrayList<Integer>();
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
TreeNode top = null;
while( cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
// System.out.println(cur);
cur = cur.left;
}
TreeNode pre = stack.peek();
//mylist.add(pre.val);
if(pre.right == null || pre.right == top){
TreeNode pres = stack.pop();
mylist.add(pres.val);
top = pre;
}else{
cur = pre.right;
}
}
return mylist;
}
}