Queue & circular queue
Queue: first in first out linear table. When we discuss the sequential storage implementation of queues, we need to allocate an array space for it. And two pointers, Q.front and Q.rear. Where Q.rear points to the tail of the team, that is, the position where we insert the element; Q. Front points to the head of the team, which is where we delete the element. Every time we complete an insert or delete operation, Q.rear or Q.front needs to add 1, that is, move back one grid and point to the next element that can be inserted or deleted.
The problem we will face: false overflow
The left figure shows the queue just after initialization. There are no elements. Both pointers point to the position where the index of the array is 0, indicating that the queue is empty at this time. At this time, the queue can insert elements but not delete elements, and the inserted elements are located at the position pointed by Q.rear.
The figure in the figure is what it looks like when three elements are inserted and the elements have not been deleted. At this time, the position of the next insertable element is at the position pointed by Q.rear (that is, the position with array subscript 3), and the position of the next delectable element (in fact, it is the first element, because the element has not been deleted) is at the position pointed by Q.front (that is, the position with array subscript 0).
The figure on the right shows what it looks like when three elements are inserted and two elements are deleted on the basis of the figure in the middle. At this time, the element can still be deleted, but the element can no longer be inserted, because the subscript pointed to by Q.rear has reached the MAXSIZE of the array (that is, overflow). However, we can obviously find that there is still unused space in the array, that is, the space vacated after deleting two elements. We call this situation "false overflow".
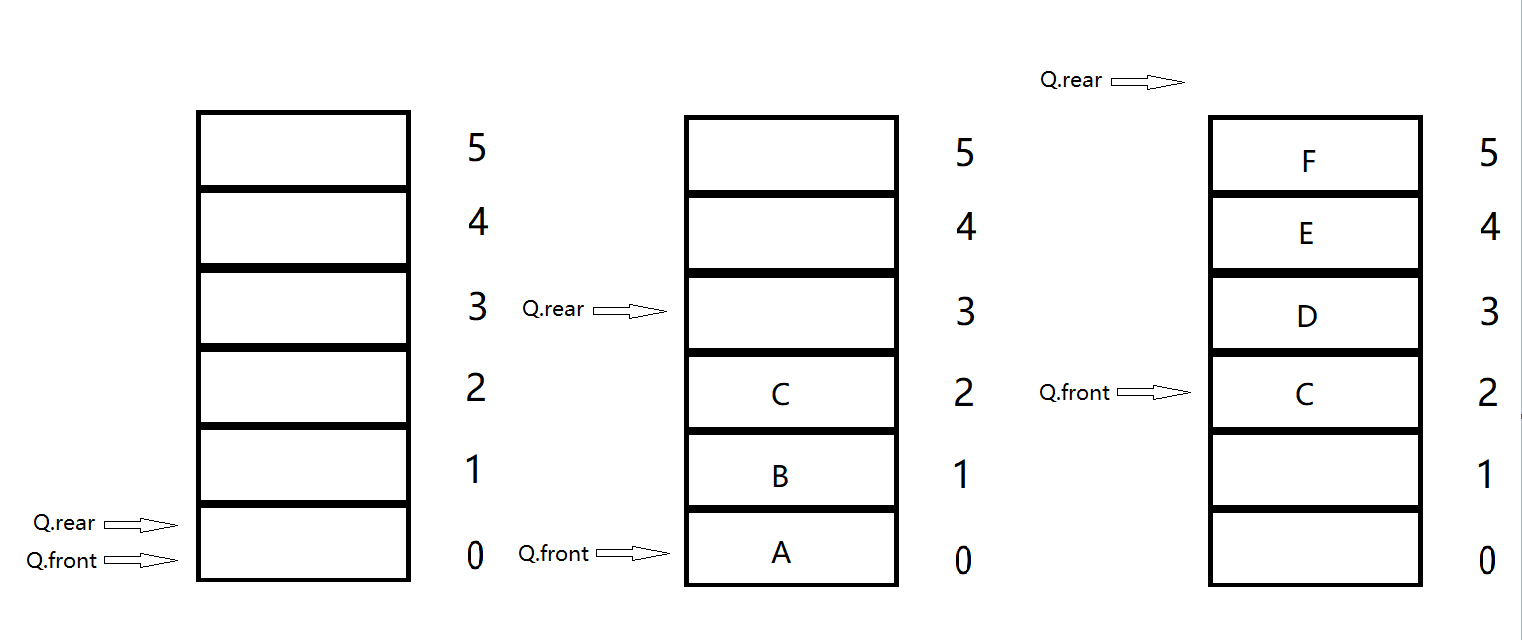
We use circular queues to solve the "false overflow" problem.
The circular queue can achieve this effect: in the above right figure, after inserting element F, the pointer Q.rear points to the position where the index of the array is 0. That is, under the condition that the array is "not full", the Q.rear and Q.front pointers loop within the array. Similar to the circular linked list, the next lattice of the last lattice of the array is the first lattice of the array.
Circular queue: why should I quote the word "not full" above? This is because in order to achieve the effect of circular queue, we need to make a new definition of the "queue full" state of circular queue.
First, we still define the state when "Q.front==Q.rear" is empty. There are two situations to reach this state. The first is that after just initializing the circular queue, both Q.front and Q.rear point to the first lattice of the array. At this time, we call the circular queue empty. In the second case, after deleting an element, there are no more elements in the queue. At this time, the queue is obviously empty. As shown in the figure below, after deleting element D, Q.front will catch up with Q.rear, so they are equal. At this time, we call the circular queue empty. Obviously, there are and only these two situations that make the team empty, so it is reasonable to judge the team empty with "Q.front==Q.rear".
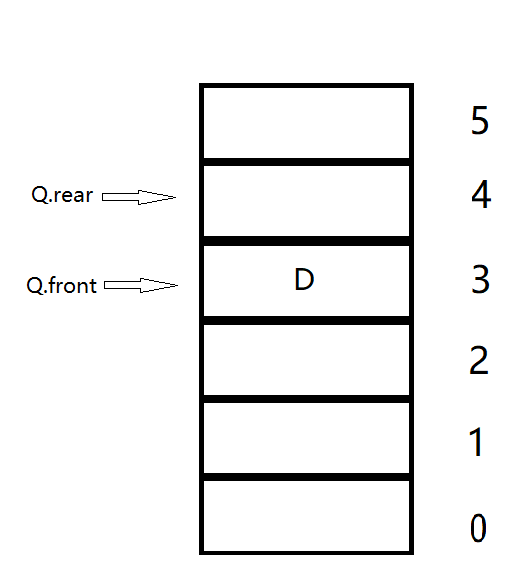
However, we will find that if we do not change the definition of "full queue", that is, the definition of "Q.rear==MAXSIZE", the circular queue will never reach the state of "full". This is because in the circular queue, when the pointer Q.rear points to the array subscript MAXSIZE-1, its next step will return to 0, so it will always be less than MAXSIZE.
However, before changing the definition of "queue full", we need to change the changes of the two pointers after inserting and deleting elements. In order to make the two pointers return to 0 after reaching MAXSIZE-1, we changed the original operation (that is, add 1 directly, and then the two pointers point to the next grid respectively) to "mold MAXSIZE after adding 1", that is, Q.rear=(Q.rear+1)%MAXSIZE,Q.front=(Q.front+1)%MAXSIZE. This change allows two pointers to loop through the array.
Next, we will find that when all spaces have elements, it reaches the state of "full queue", but at this time, Q.front==Q.rear, that is, at this time, the queue is obviously full, but the computer will think it is empty. As shown in the figure below, after inserting element C, the queue is actually full, but the two pointers meet, so the computer thinks the queue is empty.
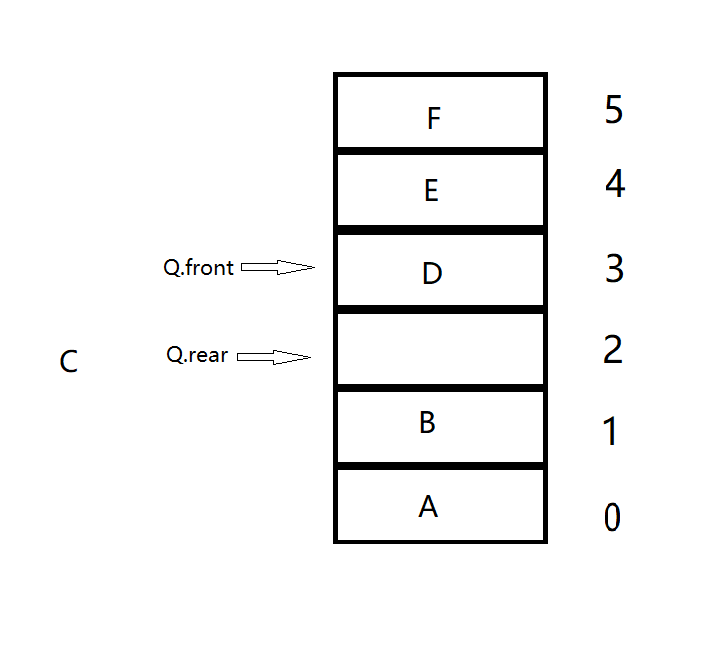
In order to solve this problem, we need to sacrifice a grid, that is, artificially make the two pointers never meet because the team is full. Therefore, our definition of round robin queue full is "(Q.rear+1)%MAXSIZE==Q.front". This definition means that if two pointers meet because I insert this element, then the queue is full at this time, and my insertion operation is illegal.
Conclusion: in order to solve the "false overflow problem" of ordinary queues, we use circular queues.
The judgment conditions of various operations and states of ordinary queue and circular queue are inconsistent. Their respective judgment conditions are given below.
Ordinary queue: ① after inserting elements: Q.rear + +; ② After deleting elements: Q.front + +;
③ team air: Q.front==Q.rera; ④ Team full: Q.rear==MAXSIZE; ⑤ Captain: Q.rear-Q.front.
Circular queue: ① after inserting elements: Q.rear=(Q.rear+1)%MAXSIZE;
② after deleting elements: Q.front=(Q.front+1)%MAXSIZE;
③ team air: Q.front==Q.rera; ④ Team full: (Q.rear+1)%MAXSIZE==Q.front;
⑤ team leader: (Q.rear+MAXSIZE-Q.front)%MAXSIZE
The following is the code implementation of the basic operation of circular queue, the solution of SCAU8584 and two solutions of SCAU8590.
//Function of this project: complete the basic operation of circular queue and SCAU8584 and SCAU8590
#include <stdio.h>
#include <malloc.h>
#define QElemType int
#define Status int
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXQSIZE 100
typedef struct
{
QElemType *base;
int front;
int rear;
}SqQueue;
Status InitQueue(SqQueue &Q)
{
Q.base=new QElemType[MAXQSIZE];
Q.front=0;
Q.rear=0;
return OK;
}
Status DestroyQueue(SqQueue &Q)
{
delete Q.base;
Q.front=0;
Q.rear=0;
return OK;
}
Status ClearQueue(SqQueue &Q)
{
Q.rear=Q.front;
return OK;
}
Status QueueEmpty(SqQueue Q)
{
if(Q.front==Q.rear) return TRUE;
else return FALSE;
}
int QueueLength(SqQueue Q)
{
return (Q.rear+MAXQSIZE-Q.front)%MAXQSIZE;
}
Status GetHead(SqQueue Q, QElemType &e)
{
if(Q.rear==Q.front) return ERROR;
else e=Q.base[Q.front];
return OK;
}
Status EnQueue(SqQueue &Q,QElemType e)
{
if((Q.rear+1)%MAXQSIZE==Q.front) return ERROR;
else
{
Q.base[Q.rear]=e;
Q.rear=(Q.rear+1)%MAXQSIZE;
}
return OK;
}
Status DeQueue(SqQueue &Q, QElemType &e)
{
if(Q.rear==Q.front) return ERROR;
else
{
e=Q.base[Q.front];
Q.front=(Q.front+1)%MAXQSIZE;
}
return OK;
}
Status QueueTraverse(SqQueue Q)
{
if(Q.front==Q.rear) printf("The Queue is Empty!");
else
{
int i=Q.front;
printf("The Queue is: ");
while(i!=Q.rear)
{
printf("%d ",Q.base[i]);
i++;
i=i%MAXQSIZE;
}
}
printf("\n");
return OK;
}
int main()
{
/*SCAU 8584
int a;
SqQueue S;
QElemType x, e;
if(InitQueue(S))
{
printf("A Queue Has Created.\n");
}
while(1)
{
printf("1:Enter \n2:Delete \n3:Get the Front \n4:Return the Length of the Queue\n5:Load the Queue\n0:Exit\nPlease choose:\n");
scanf("%d",&a);
switch(a)
{
case 1: scanf("%d", &x);
if(!EnQueue(S,x)) printf("Enter Error!\n");
else printf("The Element %d is Successfully Entered!\n", x);
break;
case 2: if(!DeQueue(S,e)) printf("Delete Error!\n");
else printf("The Element %d is Successfully Deleted!\n", e);
break;
case 3: if(!GetHead(S,e))printf("Get Head Error!\n");
else printf("The Head of the Queue is %d!\n", e);
break;
case 4: printf("The Length of the Queue is %d!\n",QueueLength(S));
break;
case 5: QueueTraverse(S);
break;
case 0: return 1;
}
}
*/
/*SCAU 8590 Queue algorithm
SqQueue Q;
InitQueue(Q);
int number_of_people;
scanf("%d",&number_of_people);
float Time[number_of_people][2];
int ArriveTime,WorkTime;
for(int i=0;i<number_of_people;i++) //The first column of the array records the arrival Time of the customer, and the second column records the handling Time of the customer
{
scanf("%d %d",&ArriveTime,&WorkTime);
Time[i][0]=ArriveTime;
Time[i][1]=WorkTime;
}
float LastFinishTime=Time[0][0]; //The timing starts when the first customer arrives
float WaitTime=0;
for(int i=0;i<number_of_people;i++) EnQueue(Q,Time[i][1]);
for(int i=0;i<number_of_people;i++)
{
DeQueue(Q,WorkTime);
if(Time[i][0]<LastFinishTime) //If you arrive before the previous customer completes, you need to wait until the previous customer completes
{
WaitTime+=LastFinishTime-Time[i][0]; //The waiting time is the time of the last completion minus the time of your arrival
LastFinishTime+=WorkTime; //The time of completion is equal to the time of the previous completion plus the time spent by yourself, because after the previous completion, you will follow the business
}
else LastFinishTime=Time[i][0]+WorkTime; //When you don't need to wait, the completion time is equal to the time you arrive plus the time you spend on business
}
printf("%.2f",WaitTime/number_of_people);
*/
/*SCAU 8590 General algorithm
int number_of_people;
scanf("%d",&number_of_people);
float ArriveTime,WorkTime,WaitTime=0;
float Time[number_of_people][3];
for(int i=0;i<number_of_people;i++) //The first column of the array records the arrival Time of the customer, the second column records the handling Time of the customer, and the third column records the completion Time of the customer.
{
scanf("%f %f",&ArriveTime,&WorkTime);
Time[i][0]=ArriveTime;
Time[i][1]=WorkTime;
}
Time[0][2]=Time[0][0]+Time[0][1]; //The time for the first customer to complete the processing is his arrival time plus the time he needs to process
for(int i=1;i<number_of_people;i++)
{
if(Time[i][0]<=Time[i-1][2]) Time[i][2]=Time[i-1][2]+Time[i][1]; //If the customer arrives before the previous customer completes, the processing time of the customer is the completion time of the previous customer plus the time he needs to handle
else Time[i][2]=Time[i][0]+Time[i][1]; //If the customer arrives after the previous customer completes the processing, the time for the customer to complete the processing is his arrival time plus the time he needs to process
}
for(int i=1;i<number_of_people;i++) //Obviously, the first customer doesn't have to wait
{
if(Time[i][0]>=Time[i-1][2]); //If you arrive before the previous customer completes, you need to wait until the previous customer completes; On the contrary, there is no need to wait.
else WaitTime+=Time[i-1][2]-Time[i][0];
}
printf("%.2f",WaitTime/number_of_people);
*/
return 0;
}
Welcome to discuss and exchange!