The introduction course of algorithm of Zuo Chengyun, teacher of niuke.com

Violent recursion

principle

Hanoi Tower problem

problem

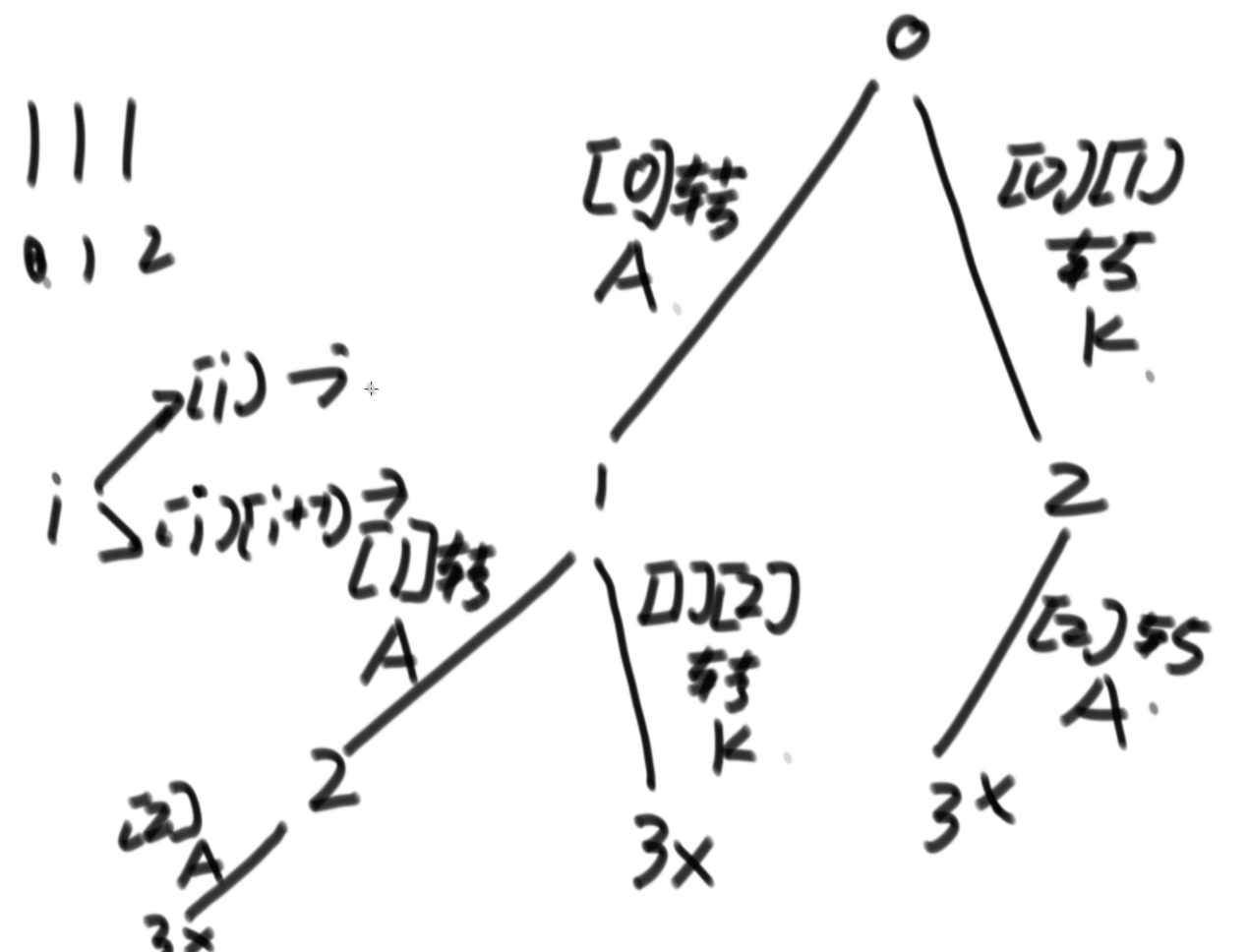
• Print the process of the n-layer Hanoi tower moving from the left to the far right

thought

There are six processes, left to right, left to middle, middle to left, middle to right, right to left, right to middle, which are nested with each other

Left to right

• Move 1 - 'N-1 to the middle bar
• Move N from leftmost to rightmost
• Move 1-N-1 to the rightmost bar

Left to center

• Move 1-N-1 from left to right
• N move from left to middle
• Move 1 - 'N-1 from right to middle

. . . . . .

code

package class08;
 
public class Code01_Hanoi {
 
    public static void hanoi(int n) {
        if (n > 0) {
            func(n, "Left", "right", "in");
        }
    }
 
    // 1~i disk target is from - > to, other is another
    public static void func(int N, String from, String to, String other) {
        if (N == 1) { // base
            System.out.println("Move 1 from " + from + " to " + to);
        } else {
            func(N - 1, from, other, to);
            System.out.println("Move " + N + " from " + from + " to " + to);
            func(N - 1, other, to, from);
        }
    }
     
     
     
     
    public static void printAllWays(int n) {
        leftToRight(n);
    }
     
    public static void leftToRight(int n) {
        if(n== 1) {
            System.out.println("Move 1 from left to right");
            return ;
        }
        leftToMid(n-1);
        System.out.println("Move " +n + " from left to right");
        midToRight(n-1);
    }
     
    public static void leftToMid(int n) {
        if(n== 1) {
            System.out.println("Move 1 from left to mid");
            return ;
        }
        leftToRight(n-1);
        System.out.println("Move " +n + " from left to mid");
        rightToMid(n-1);
    }
     
    public static void midToRight(int n) {
         
    }
     
    public static void rightToMid(int n) {
         
    }
     
     
     
     
     
     
     
     
     
     
     
 
    public static void main(String[] args) {
        int n = 3;
        hanoi(n);
    }
 
}

example

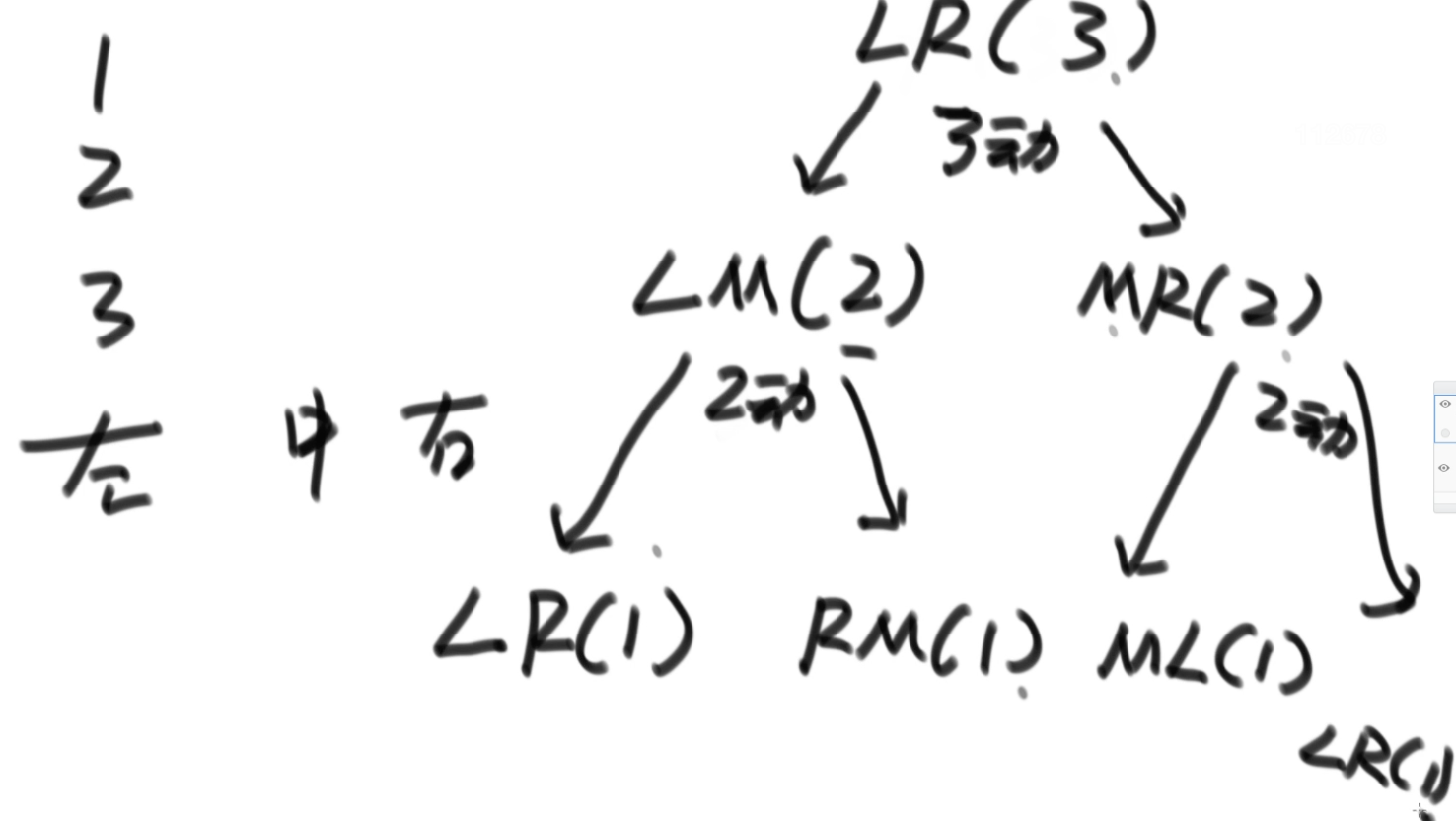
Print all subsequences of a string, including empty strings

(models tried from left to right)

• Need to ensure the order of characters before and after
• "abc" =>a,b,c,ab,ac,bc,abc,null
• brutal force

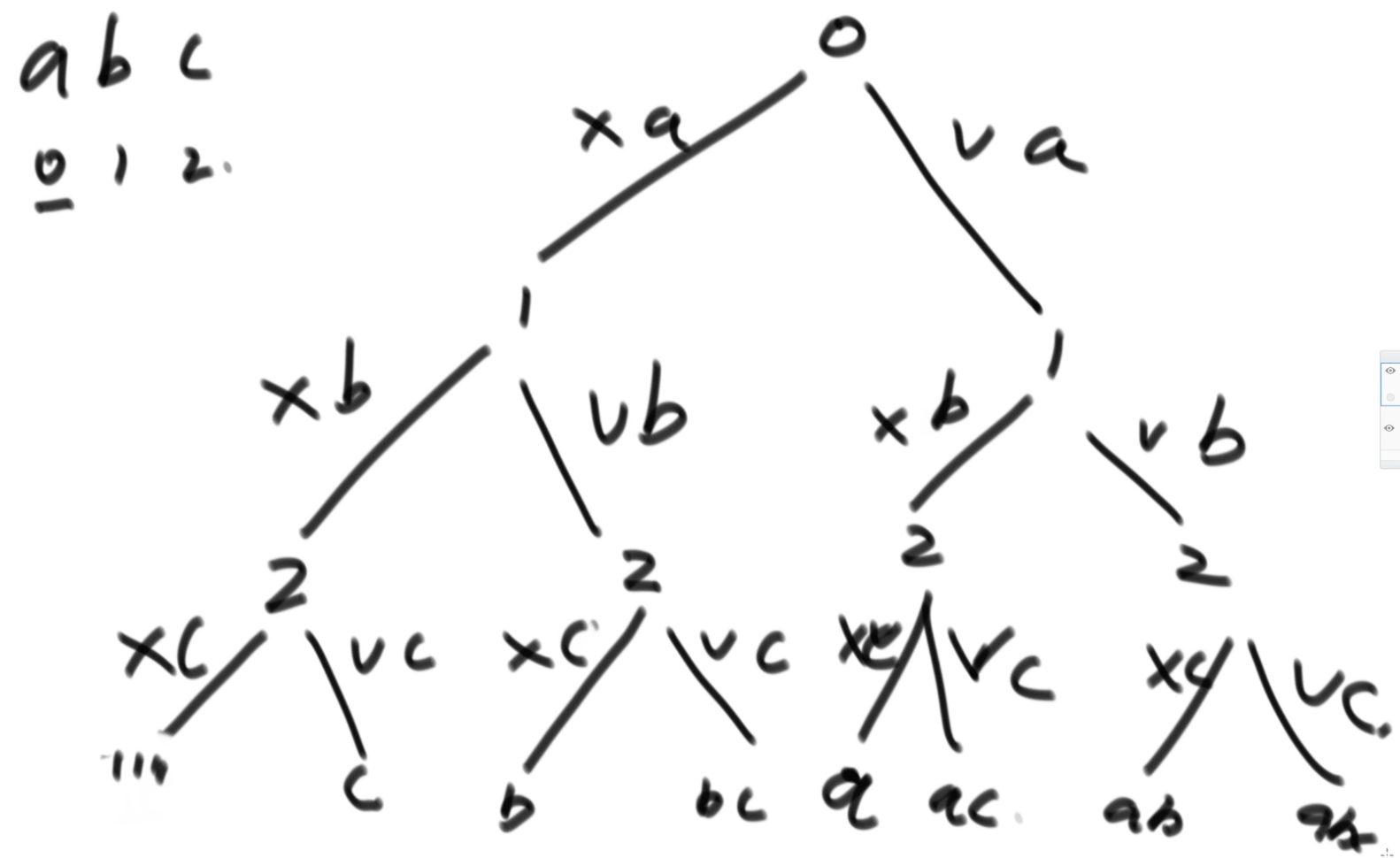Print all strings

thinking

• Full arrangement. The characters previously selected cannot be selected later.

code

package class08;

import java.util.ArrayList;
import java.util.HashSet;
import java.util.List;

public class Code03_PrintAllPermutations {

	public static ArrayList<String> Permutation(String str) {
		ArrayList<String> res = new ArrayList<>();
		if (str == null || str.length() == 0) {
			return res;
		}
		char[] chs = str.toCharArray();
		process(chs, 0, res);
		return res;
	}

	// All characters in the str[i..] range can be in the i position, and will be tried later
	// In the scope of str[0..i-1], it is the previous choice
	// Please add all the strings into res
	public static void process(char[] str, int i, ArrayList<String> res) {
		if (i == str.length) {
			res.add(String.valueOf(str));
		}
		boolean[] visit = new boolean[26]; // visit[0 1 .. 25]
		for (int j = i; j < str.length; j++) {
			if (!visit[str[j] - 'a']) {
				visit[str[j] - 'a'] = true;
				swap(str, i, j);
				process(str, i + 1, res);
				swap(str, i, j);
			}
		}
	}

	public static void swap(char[] chs, int i, int j) {
		char tmp = chs[i];
		chs[i] = chs[j];
		chs[j] = tmp;
	}

	public static List<String> getAllC(String s) {
		List<String> ans = new ArrayList<>();
		ArrayList<Character> set = new ArrayList<>();
		for (char cha : s.toCharArray()) {
			set.add(cha);
		}
		process(set, "", ans);
		return ans;
	}

	public static void process(ArrayList<Character> list, String path, List<String> ans) {
		if (list.isEmpty()) {
			ans.add(path);
			return;
		}
		HashSet<Character> picks = new HashSet<>();
		//Each character in the set can be used as the current character, but once the current decision is made, it cannot be used again (de duplicated)
		for (int index = 0; index < list.size(); index++) {
			if (!picks.contains(list.get(index))) {
				picks.add(list.get(index));
				String pick = path + list.get(index);
				ArrayList<Character> next = new ArrayList<>(list);
				next.remove(index);
				process(next, pick, ans);
			}
		}
	}

	public static void main(String[] args) {
		String s = "aac";
		List<String> ans = getAllC(s);
		for (String str : ans) {
			System.out.println(str);
		}
	}

}

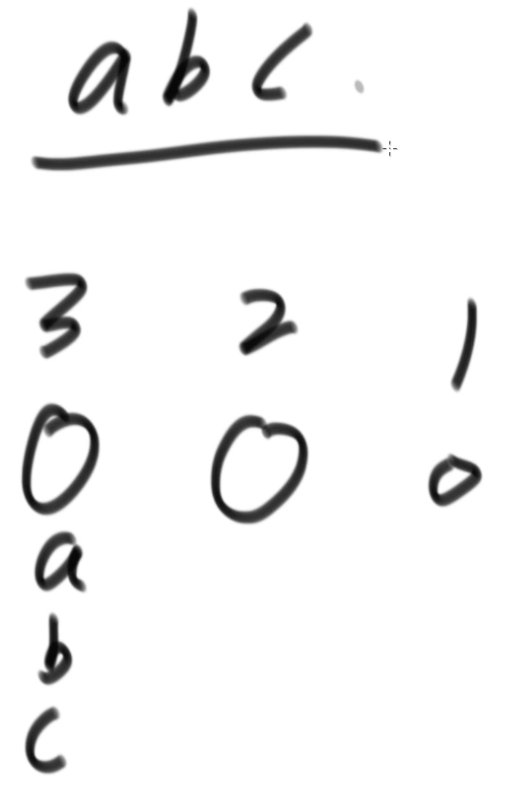
Digital transformation

Title Requirements

Thinking

• Input the original string 111, and 012 below corresponds to its position. For the i-th node, I can implement the transformation by itself or with i+1

• But you need to decide if i and i+1 exceed 26, because 26 represents z

• When encountering 0, judge: for example, "102". If 1 makes a decision on its own, then 0 can't make a decision on its own, and 0 and 2 can't make a decision, so 0 can only be with and together, which is effective

code

package class08;

public class Code06_ConvertToLetterString {

	public static int number(String str) {
		if (str == null || str.length() == 0) {
			return 0;
		}
		return process(str.toCharArray(), 0);
	}

	// i. how to transform the previous position has been decided. No need to worry about it
	// How many kinds of conversion results does str[i...]
	public static int process(char[] str, int i) {
		if (i == str.length) { // base case
			//To the end, the previous path represents an effective method
			return 1;
		}
		// i not to end
		if (str[i] == '0') {//In the case of "102", 0 can't make a decision
			return 0;
		}
		// str[i] character is not '0'
		if (str[i] == '1') {
			int res = process(str, i + 1); // i as a separate part, how many methods can i follow
			if (i + 1 < str.length) {
				res += process(str, i + 2); // (i and i+1) as separate parts, how many methods are there in the future
			}
			return res;
		}
		if (str[i] == '2') {
			int res = process(str, i + 1); // i as a separate part, how many methods can i follow
			// (i and i+1) as separate parts and no more than 26, how many methods are there in the future
			if (i + 1 < str.length && (str[i + 1] >= '0' && str[i + 1] <= '6')) {
				res += process(str, i + 2); // (i and i+1) as separate parts, how many methods are there in the future
			}
			return res;
		}
		// str[i] == '3' ~ '9'
		return process(str, i + 1);
	}

	public static int dpWays(String s) {
		if (s == null || s.length() == 0) {
			return 0;
		}
		char[] str = s.toCharArray();
		int N = str.length;
		int[] dp = new int[N + 1];
		dp[N] = 1;
		for (int i = N - 1; i >= 0; i--) {
			if (str[i] == '0') {
				dp[i] = 0;
			} else if (str[i] == '1') {
				dp[i] = dp[i + 1];
				if (i + 1 < N) {
					dp[i] += dp[i + 2];
				}
			} else if (str[i] == '2') {
				dp[i] = dp[i + 1]; 
				if (i + 1 < str.length && (str[i + 1] >= '0' && str[i + 1] <= '6')) {
					dp[i] += dp[i + 2];
				}
			} else {
				dp[i] = dp[i + 1];
			}
		}
		return dp[0];
	}

	public static void main(String[] args) {
		System.out.println(number("11111"));
	}

}

knapsack problem

Title Requirements

code

package class08;

public class Code07_Knapsack {

	public static int getMaxValue(int[] w, int[] v, int bag) {
		return process(w, v, 0, 0, bag);
	}

	// index the goods number of the current goods
	//w [index] weight of current goods
	//v [index] value of current goods
	//Already made decisions from alreadyW: 0 to index-1, resulting in the current weight
	//Bag: total weight of bag (fixed parameter)
	//index. . .  Free choice of all subsequent goods, return the maximum value
	public static int process(int[] w, int[] v, int index, int alreadyW, int bag) {
		if (alreadyW > bag) {//It's overweight
			return -1;
		}
		// The weight is not over
		if (index == w.length) {
			return 0;
		}
		int p1 = process(w, v, index + 1, alreadyW, bag);//Maximum value obtained without current index goods
		int p2next = process(w, v, index + 1, alreadyW + w[index], bag);//For current goods, the value of current goods + subsequent value
		int p2 = -1;
		if (p2next != -1) {
			p2 = v[index] + p2next;
		}
		return Math.max(p1, p2);

	}

	public static int maxValue(int[] w, int[] v, int bag) {
		return process(w, v, 0, bag);
	}

	// There's only rest left,
	// index... Free choice of goods, but not more than rest space
	// Return to the maximum value you can get
	public static int process(int[] w, int[] v, int index, int rest) {
		if (rest <= 0) { // base case 1
			return 0;
		}
		// rest >=0
		if (index == w.length) { // base case 2
			return 0;
		}
		// There's space and goods
		int p1 = process(w, v, index + 1, rest);
		int p2 = Integer.MIN_VALUE;
		if (rest >= w[index]) {
			p2 = v[index] + process(w, v, index + 1, rest - w[index]);
		}
		return Math.max(p1, p2);
	}

	public static int dpWay(int[] w, int[] v, int bag) {
		int N = w.length;
		int[][] dp = new int[N + 1][bag + 1];
		for (int index = N - 1; index >= 0; index--) {
			for (int rest = 1; rest <= bag; rest++) {
				dp[index][rest] = dp[index + 1][rest];
				if (rest >= w[index]) {
					dp[index][rest] = Math.max(dp[index][rest], v[index] + dp[index + 1][rest - w[index]]);
				}
			}
		}
		return dp[0][bag];
	}

	public static void main(String[] args) {
		int[] weights = { 3, 2, 4, 7 };
		int[] values = { 5, 6, 3, 19 };
		int bag = 11;
		System.out.println(maxValue(weights, values, bag));
		System.out.println(dpWay(weights, values, bag));
	}

}

Licensing

thinking

• In the first case, when there is only one card left, you can take the last card directly

• If I take the leftmost card, my score is arr [l] + S (arr, L+1, R)

• If I take the right most card, my score is arr [R] + S (arr, L, R-1)

• For the above two cases, the maximum value is my choice

• Where S is the black box function, because the first hand and the second hand are interchangeable roles. When the first hand finishes playing, its role becomes the second hand

code

package class08;

public class Code08_CardsInLine {

	public static int win1(int[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		return Math.max(f(arr, 0, arr.length - 1), s(arr, 0, arr.length - 1));
	}

	public static int f(int[] arr, int i, int j) {
		if (i == j) {
			return arr[i];
		}
		return Math.max(arr[i] + s(arr, i + 1, j), arr[j] + s(arr, i, j - 1));
	}

	public static int s(int[] arr, int i, int j) {
		if (i == j) {
			return 0;//There is no card for the backhand
		}
		return Math.min(f(arr, i + 1, j), f(arr, i, j - 1));//Let the other side get the minimum value
	}

	public static int win2(int[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		int[][] f = new int[arr.length][arr.length];
		int[][] s = new int[arr.length][arr.length];
		for (int j = 0; j < arr.length; j++) {
			f[j][j] = arr[j];
			for (int i = j - 1; i >= 0; i--) {
				f[i][j] = Math.max(arr[i] + s[i + 1][j], arr[j] + s[i][j - 1]);
				s[i][j] = Math.min(f[i + 1][j], f[i][j - 1]);
			}
		}
		return Math.max(f[0][arr.length - 1], s[0][arr.length - 1]);
	}

	public static void main(String[] args) {
		int[] arr = { 1, 9, 1 };
		System.out.println(win1(arr));
		System.out.println(win2(arr));

	}

}

N-queens problem

thinking

• If the position of the previous queen is (a, b), then the position of the next queen is (c, d), because it is executed from top to bottom, it can ensure that each queen does not walk together

• By comparing b and d to determine whether the queens are in the same column

• Determine whether it is on a slash by comparing | c-a|==|d-b|

code

package class08;

public class Code09_NQueens {

	public static int num1(int n) {
		if (n < 1) {
			return 0;
		}
		// record[0] ?  record[1]  ?  record[2]
		int[] record = new int[n]; // Record [i] - > the queen of line I, in the column
		return process1(0, record, n);
	}

	// Subtext: the queen of record[0..i-1], any two queens must not be in the same row, column or diagonal
	// Now i'm in line i
	// record[0..i-1] indicates the previous line and the Queen's position
	// n represents the total number of lines
	// The return value is, after all the queens are placed, how many kinds of reasonable placement methods are there
	public static int process1(int i, int[] record, int n) {
		if (i == n) { // Terminate line
			return 1;
		}
		int res = 0;
		for (int j = 0; j < n; j++) { // The current row is in row i, try all the columns in row i - > J
			// Will the current queen of row I, placed in column j, and the previous queen of row (0..i-1), not be co listed or co slashed,
			// If yes, considered valid
			// If not, it is considered invalid
			if (isValid(record, i, j)) {
				record[i] = j;
				res += process1(i + 1, record, n);
			}
		}
		return res;
	}

	// record[0..i-1] you need to see, record[i..] don't need to see
	// Return row i queen, put in column j, is it valid
	public static boolean isValid(int[] record, int i, int j) {
		for (int k = 0; k < i; k++) { // The queen of a previous k-line
			if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {
				return false;
			}
		}
		return true;
	}

	// Please do not exceed 32 queen questions. If the type is changed to long, 64 queen questions can be calculated
	public static int num2(int n) {
		if (n < 1 || n > 32) {
			//throw new RuntimeException("the problem is too big to calculate");
			//Run error: no try catch and throw declaration
			//Expected error: use try catch, for example, to catch an exception and then tell the consumer that the input type is wrong 
			return 0;
		}
		int limit = n == 32 ? -1 : (1 << n) - 1;
		return process2(limit, 0, 0, 0);
	}

	//Recursive use of optimized version and binary type calculation
	// colLim column limit, the position of 1 can't put queen, the position of 0 can
	// Limit of leftDiaLim left slash, position of 1 can't put queen, position of 0 can
	// Limit of rightDiaLim right slash, position of 1 can't put queen, position of 0 can
	public static int process2(int limit, 
			int colLim, 
			int leftDiaLim,
			int rightDiaLim) {
		if (colLim == limit) { // base case
			return 1;
		}
		// All the queen candidates are on the pos
		int pos = limit & (~(colLim | leftDiaLim | rightDiaLim));
		int mostRightOne = 0;
		int res = 0;
		while (pos != 0) {
			mostRightOne = pos & (~pos + 1);
			pos = pos - mostRightOne;
			res += process2(limit, 
					colLim | mostRightOne,
					(leftDiaLim | mostRightOne) << 1,
					(rightDiaLim | mostRightOne) >>> 1);
		}
		return res;
	}

	public static void main(String[] args) {
		int n = 14;

		long start = System.currentTimeMillis();
		System.out.println(num2(n));
		long end = System.currentTimeMillis();
		System.out.println("cost time: " + (end - start) + "ms");

		start = System.currentTimeMillis();
		System.out.println(num1(n));
		end = System.currentTimeMillis();
		System.out.println("cost time: " + (end - start) + "ms");

	}
}