Dijkstra runs fast on the positive weight graph, but it can't solve the shortest path with negative weight, as shown in the following figure:

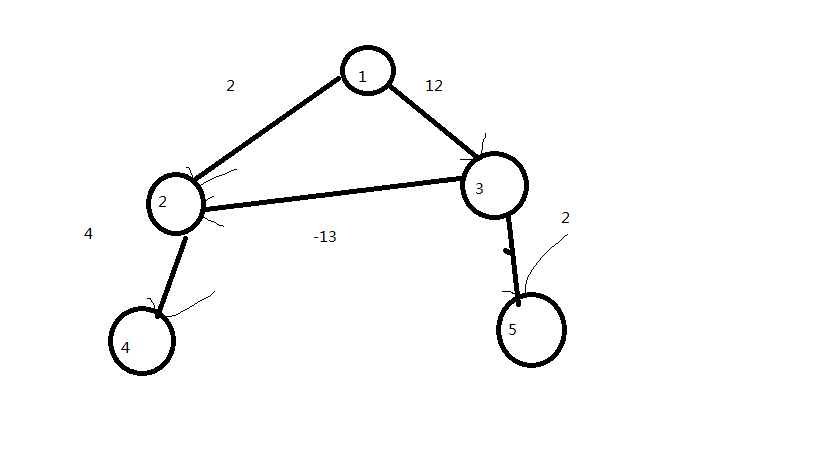
The result of Dijkstra's running is (with 1 as the origin): 0.212 6 14;

But the result of manual calculation, dist[4], is obviously 5. Why does this happen? The reason is obvious. Dijkstra thinks that coming from a longer side is not shorter than coming from a shorter side However, due to the presence of a negative weight edge, it can be "saved", just like relaxing node 2.

Bellman_Ford:

Now that we know why Dijkstra can't make a negative weight graph, let's take a look at the bellman Ford algorithm. Its basic idea is: the shortest path of a graph does not contain a positive ring (can not walk), nor can it have a negative ring (otherwise it can walk infinitely small). Therefore, it passes through n-1 edges at most (every node passes through once). In fact, Bellman Ford enumerates how many edges are away from the source point and tries to relax each edge. Please contact the figure above to deduce the operation process of Bellman Ford

An example is as follows:

5 5
1 2 2
1 3 12
3 2 -13
2 4 4
3 5 2

The time complexity of the simple Bellman Ford algorithm is O(NM), and the program is as follows:

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
int n,m,s,dist[100001],v[200005],w[200005],u[200005],cnt,x,y,z;
void bellman_ford(int s)
{
    memset(dist,20,sizeof(dist));
    dist[s]=0;
    for(int i=1;i<=n-1;i++)
    {
    	for(int j=1;j<=m;j++)
    	{
    		dist[v[j]]=min(dist[v[j]],dist[u[j]]+w[j]);
		}
	}
}
int main()
{
    scanf("%d %d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d %d %d",&u[i],&v[i],&w[i]);
    }
    bellman_ford(1);
    for(int i=1;i<=n;i++)
    {
        cout<<dist[i]<<" ";
    }
    return 0;
}

SPFA:

SPFA is the optimization of Bellman Ford algorithm. It uses queue to save the nodes that will relax other points. Each time, it selects the points connected with the head of the queue to relax. It can be realized by using chain forward star (adjacency table), which avoids many invalid relaxation operations of Bellman Ford algorithm. The average complexity O(KM), K is the average number of times of relaxation, and it may also be returned to O(NM) by grid chart, which is unstable Algorithm. The procedure is as follows:

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
int n,m,s,dist[100001],v[200005],w[200005],nxt[200005],head[200005],cnt,x,y,z;
bool vis[100001];
void add(int a,int b,int c)
{
    v[++cnt]=b;
    w[cnt]=c;
    nxt[cnt]=head[a];
    head[a]=cnt;
}
void SPFA(int s)
{
    memset(dist,20,sizeof(dist));
   	queue<int>q;
    dist[s]=0;
    vis[s]=1;
	q.push(s);
    while(!q.empty())
    {
        int c=q.front();
        q.pop();
        vis[c]=0;
        for(int i=head[c];i;i=nxt[i])
        {
            int y=v[i];
            if(dist[y]>=dist[c]+w[i])
            {
                dist[y]=dist[c]+w[i];
                if(!vis[y])
                {
                	q.push(y);
                	vis[y]=1;
				}
            }
        }
    }
}
int main()
{
    scanf("%d %d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z);
    }
    SPFA(1);
    for(int i=1;i<=n;i++)
    {
        cout<<dist[i]<<" ";
    }
    return 0;
}