BFPRT

The bfprt algorithm is used to find the smallest k element in the array. The bfprt algorithm can find the answer in O(n) time.

Algorithmic Ideas

We already have a good general algorithm for finding the smallest k element in an array. This algorithm is O(n) in the best case, but O(n^2) in the worst case. In fact, the bfprt algorithm is improved on this basis.

General Solution

We randomly select a number in the array as the partition value, then do a quick partation process (put the number less than numbers to the left of the array, the number equal to numbers in the middle of the array, the number greater than numbers to the right of the array), and then determine the relative relationship between k and the area equal to numbers, if k happens to be in theIf k is on the left side of the numbered region, we recursively do the above process on the left side. If k is on the right side of the numbered region, we recursively do the same process on the right side.

For a general solution, let's analyze its time complexity:

Recursive function complexity calculation:

T(N)=a*T(N/b)+o(N^d);
When log(b,a)>d, the complexity is O(N^log(b,a));
Complexity is O (N^d*log(2,N)) when log(b,a)=d;
Complexity is O (N^d) when log(b,a)<d;
N is the number of sample data, that is, the number of elements in the array.
N/b divides the number of N into smaller parts, and the number of sample data for each part is generally equal, so B equals 2.
A is the number of times a small part is executed after it has been divided into parts.
d is the time complexity of the operation remaining after the recursive function call is completed.

For the best case: each time the selected number is exactly in the middle of the array, a equals 1, b equals 2, a n d for the partation process, time complexity is O(n), so D equals 1.So T(N) = T(N/2) + O(N), where log (2, 1) < 1, the time complexity is O(N).

For the worst case scenario: each time the selected number is at the very edge of the array, the time complexity is O (N ^ 2).

The bfprt algorithm writes on this number, and the bfprt algorithm ensures that each selected number is in the middle of the array, so the time complexity is O(N).

bfprt solution:

The only difference between the bfprt solution and the general solution is that the selection of numbers is the same everywhere else, so we only talk about the process of selecting numbers.

Step 1: We will divide an array into groups of every five adjacent numbers, followed by groups of numbers if not more than five.

Step 2: For each number of groups, we find the medians of these five numbers and form a median array (median array) of all groups.

Step 3: Let's work out the median in this median array, and that number is the median.

Step 4: With this number for the partation process, the following is the same as the general solution.

Next, we analyze why the bfprt algorithm is able to be in the middle of the array each time a number is selected.

Let's assume this is the number of groups that are divided, and each column represents a group.

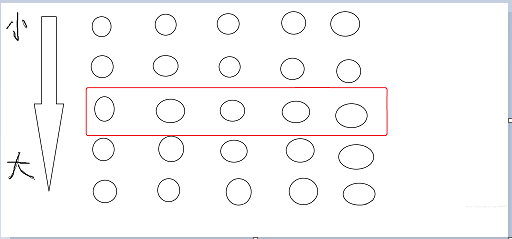
The number in the red box in the graph is assumed to be the median of each group.If we assume that the number of numbers in the total array is N, then the number of numbers in the median array is N/5.

Let's assume that the number boxed in blue is the median of the median array. The nature of the median tells us that half of the median array is larger than the divide, so there are N / 10 numbers larger than the divide.

The number outlined in the purple box is certainly larger than the divide, so at least N / 10 + (2*N) / 10 = (3*N) / 10 is larger than the divide, so the partation process with divides allows the divide to be close to the middle of the array and, at worst, at the (3*N) / 10 or (7*N) / 10 of the array.The time complexity is O(N).From this article https://blog.csdn.net/qq_40938077/article/details/81213820#commentsedit 

The code is as follows:
 

#include<bits/stdc++.h>
using namespace std;
int a[2];
int bfprt(int root[],int begin,int end,int k);//This is the core function to find the k th smallest element from the begin position to the end position of the root array
int getmedian(int root[],int beginI,int endI)//This function calculates the median from beginI to endI in the root array (actually, the median in the group divided by every five numbers)
{
    sort(root+beginI,root+endI+1);
    int sum=beginI+endI;
    int mid=(sum/2)+(sum%2);//This place is added with sum%2 to ensure that even numbers require the second of the middle two
    return root[mid];
}
int medianOfMedians(int root[],int star,int finish)//This function divides the star t to finish position of the root array into groups of five and finishes the median within each group.
{
    int num=finish-star+1;//Find Length
    int offset=num%5==0?0:1;//Finally, if there are fewer than five left, we'll divide it into a group and treat it the same way as before.
    int range=num/5+offset;
    int median[range];//This array stores the median within each group
    for(int i=0;i<range;i++)//Fill in the median array in turn
    {
        int beginI=star+i*5;//The number of groups i corresponds to the position on the root array
        int endI=beginI+4;
        median[i]=getmedian(root,beginI,min(endI,finish));
    }
    return bfprt(median,0,range-1,range/2);//Find the median of the generated median array as the partition value of the partation function
}
void swap(int root[],int a,int b)
{
    int temp=root[a];
    root[a]=root[b];
    root[b]=temp;
}
void partation(int root[],int beginJ,int endJ,int number)//The partation function requires a range equal to number
{
    int less=beginJ-1;
    int more=endJ+1;
    int cur=beginJ;
    while (cur<more)
    {
        if(root[cur]<number)
        {
            less++;
            swap(root,cur,less);
            cur++;
        }
        else if(root[cur]==number)
            cur++;
        else
        {
            more--;
            swap(root,cur,more);
        }
    }
    a[0]=less+1;
    a[1]=more-1;
}
int bfprt(int root[],int begin,int end,int k)
{
    if(begin==end)//Return directly when there is only one number in the array
        return root[begin];
    int divide=medianOfMedians(root,begin,end);//Find out which number to divide
    partation(root,begin,end,divide);//Note that after the partation process, the root array is no longer out of order
    if(k>=a[0]&&k<=a[1])//If the number required is exactly equal to the region, return root[k]
        return root[k];
    else if(k<a[0])//At this point we're looking for a smaller number than the divide, the first half of the recursion
        return bfprt(root,begin,a[0]-1,k);
    else if(k>a[1])//The number we're looking for is larger than the divide, the second half of the recursion
        return bfprt(root,a[1]+1,end,k);
}
int main()
{
    int n,k;
    int root[100000];
    while (cin>>n)
    {
        cin>>k;
        for(int i=0;i<n;i++)
            cin>>root[i];
        cout<<bfprt(root,0,n-1,k-1)<<endl;
        memset(root,0,sizeof(root));
        memset(a,0,sizeof(a));
    }
}