Alibaba Java development manual mentioned that "in order to avoid precision loss, BigDecimal can be used for floating-point operation".
In this article, I will briefly explain the reasons for the loss of precision in floating-point operation and the common usage of BigDecimal. I hope it will be helpful to you!
BigDecimal introduction
BigDecimal can realize the operation of floating-point numbers without loss of precision. Usually, most business scenarios (such as those involving money) that require accurate floating-point calculation results are done through BigDecimal.
Nani, is there any risk of precision loss in the operation of floating-point numbers? Indeed!
Example code:
float a = 2.0f - 1.9f; float b = 1.8f - 1.7f; System.out.println(a);// 0.100000024 System.out.println(b);// 0.099999905 System.out.println(a == b);// false
Why is there a risk of loss of precision when floating-point number float or double operation?
This has a lot to do with the computer's mechanism for saving floating-point numbers. We know that the computer is binary, and when the computer represents a number, the width is limited. When the infinite circular decimal is stored in the computer, it can only be truncated, so it will lead to the loss of decimal accuracy. This explains why floating-point numbers cannot be represented exactly in binary.
For example, 0.2 in decimal system cannot be accurately converted into binary decimal:
// The process of converting 0.2 to binary number is to multiply by 2 until there is no decimal, // In this calculation process, the integer part arranged from top to bottom is the result of binary. 0.2 * 2 = 0.4 -> 0 0.4 * 2 = 0.8 -> 0 0.8 * 2 = 1.6 -> 1 0.6 * 2 = 1.2 -> 1 0.2 * 2 = 0.4 -> 0((cycle occurs) ...
For more information about floating point numbers, I suggest you take a look Fundamentals of computer system (IV) floating point number This article.
Use of BigDecimal
Alibaba Java development manual mentions that for the equivalence judgment between floating-point numbers, the basic data type cannot be compared with = = and the packaging data type cannot be judged with equals.
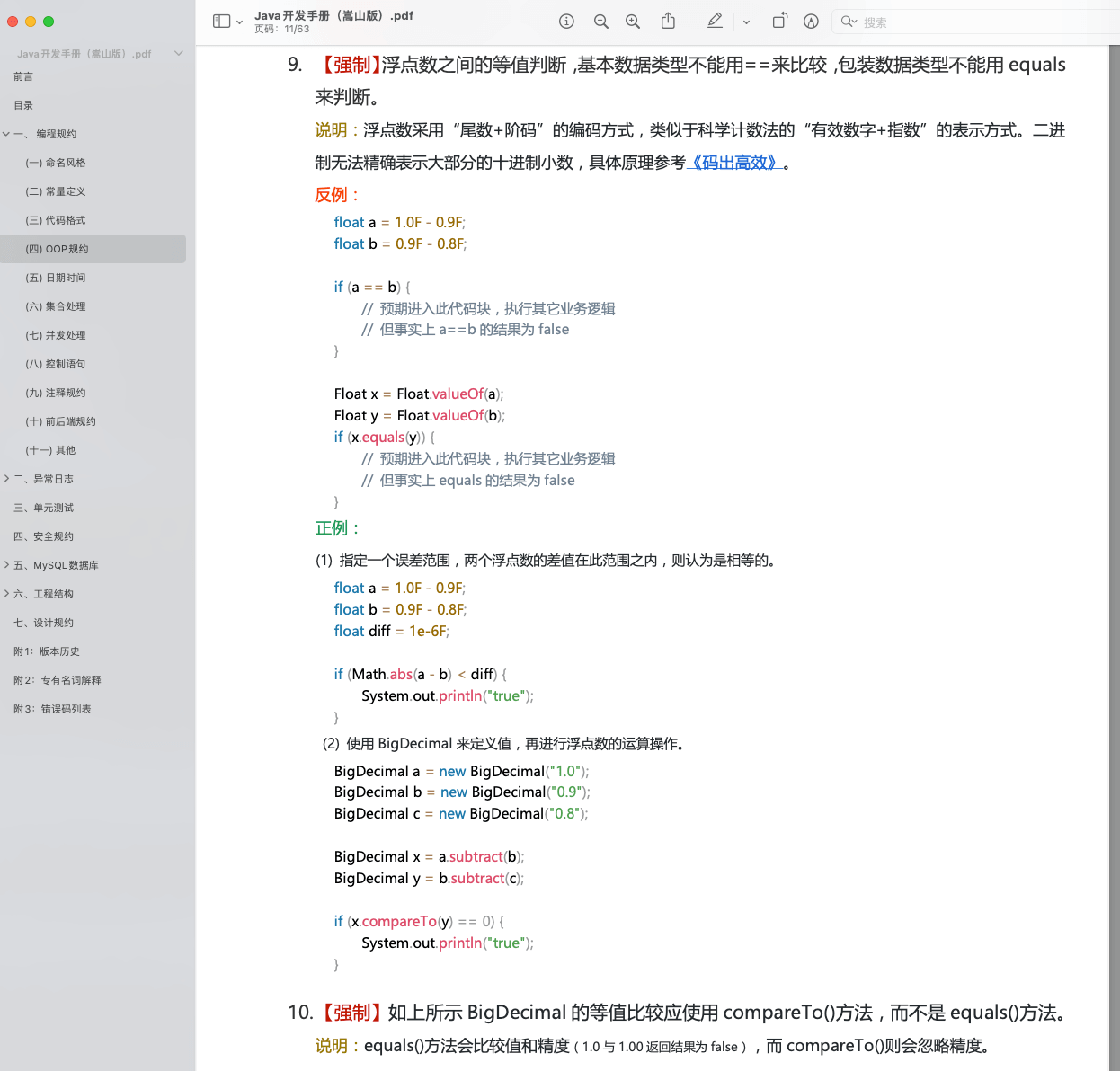
The specific reasons have been described in detail above, and will not be mentioned here. Let's take the following examples directly:
float a = 1.0f - 0.9f; float b = 0.9f - 0.8f; System.out.println(a);// 0.100000024 System.out.println(b);// 0.099999964 System.out.println(a == b);// false
From the output results, we can see the problem of precision loss.
To solve this problem, it is also very simple to directly use BigDecimal to define the value of floating-point number, and then carry out the operation of floating-point number.
BigDecimal a = new BigDecimal("1.0");
BigDecimal b = new BigDecimal("0.9");
BigDecimal c = new BigDecimal("0.8");
BigDecimal x = a.subtract(b);
BigDecimal y = b.subtract(c);
System.out.println(x); /* 0.1 */
System.out.println(y); /* 0.1 */
System.out.println(Objects.equals(x, y)); /* true */
BigDecimal common methods
add , subtract , multiply and divide
The add method is used to add two BigDecimal objects and the subtract method is used to subtract two BigDecimal objects. The multiply method is used to multiply two BigDecimal objects, and the divide method is used to divide two BigDecimal objects.
BigDecimal a = new BigDecimal("1.0");
BigDecimal b = new BigDecimal("0.9");
System.out.println(a.add(b));// 1.9
System.out.println(a.subtract(b));// 0.1
System.out.println(a.multiply(b));// 0.90
System.out.println(a.divide(b));// Unable to divide, throwing arithmetexception exception
System.out.println(a.divide(b, 2, RoundingMode.HALF_UP));// 1.11
It should be noted here that when we use the divide method, try to use three parameter versions, and do not select UNNECESSARY in the roundingmode, otherwise we may encounter arithmetics exception (when infinite circular decimal cannot be divided), where scale means to retain several decimal places, and roundingmode represents the retention rule.
public BigDecimal divide(BigDecimal divisor, int scale, RoundingMode roundingMode) {
return divide(divisor, scale, roundingMode.oldMode);
}
There are many retention rules. Here are several:
public enum RoundingMode {
// 2.5 -> 3 , 1.6 -> 2
// -1.6 -> -2 , -2.5 -> -3
UP(BigDecimal.ROUND_UP),
// 2.5 -> 2 , 1.6 -> 1
// -1.6 -> -1 , -2.5 -> -2
DOWN(BigDecimal.ROUND_DOWN),
// 2.5 -> 3 , 1.6 -> 2
// -1.6 -> -1 , -2.5 -> -2
CEILING(BigDecimal.ROUND_CEILING),
// 2.5 -> 2 , 1.6 -> 1
// -1.6 -> -2 , -2.5 -> -3
FLOOR(BigDecimal.ROUND_FLOOR),
// 2.5 -> 3 , 1.6 -> 2
// -1.6 -> -2 , -2.5 -> -3
HALF_UP(BigDecimal.ROUND_HALF_UP),
//......
}
Size comparison
a.compareTo(b): returns - 1 to indicate that a is less than B, 0 to indicate that a is equal to B, and 1 to indicate that a is greater than B.
BigDecimal a = new BigDecimal("1.0");
BigDecimal b = new BigDecimal("0.9");
System.out.println(a.compareTo(b));// 1
Keep several decimal places
Set the number of decimal places and retention rules through the setScale method. There are many retention rules. You don't need to remember them. IDEA will prompt you.
BigDecimal m = new BigDecimal("1.255433");
BigDecimal n = m.setScale(3,RoundingMode.HALF_DOWN);
System.out.println(n);// 1.255
Precautions for using BigDecimal
Note: when using BigDecimal, in order to prevent precision loss, we recommend using its BigDecimal(String val) construction method or BigDecimal Valueof (double VAL) static method to create objects.
Alibaba Java development manual also mentions this part, as shown in the figure below.

BigDecimal tool class sharing
There is a BigDecimal tool class with a large number of users on the Internet, which provides multiple static methods to simplify the operation of BigDecimal.
I have made a simple improvement and share the source code:
import java.math.BigDecimal;
import java.math.RoundingMode;
/**
* Gadget class to simplify BigDecimal calculation
*/
public class BigDecimalUtil {
/**
* Default division precision
*/
private static final int DEF_DIV_SCALE = 10;
private BigDecimalUtil() {
}
/**
* Provide accurate addition operation.
*
* @param v1 augend
* @param v2 Addend
* @return Sum of two parameters
*/
public static double add(double v1, double v2) {
BigDecimal b1 = BigDecimal.valueOf(v1);
BigDecimal b2 = BigDecimal.valueOf(v2);
return b1.add(b2).doubleValue();
}
/**
* Provide accurate subtraction.
*
* @param v1 minuend
* @param v2 Subtraction
* @return Difference between two parameters
*/
public static double subtract(double v1, double v2) {
BigDecimal b1 = BigDecimal.valueOf(v1);
BigDecimal b2 = BigDecimal.valueOf(v2);
return b1.subtract(b2).doubleValue();
}
/**
* Provide accurate multiplication.
*
* @param v1 Multiplicand
* @param v2 multiplier
* @return Product of two parameters
*/
public static double multiply(double v1, double v2) {
BigDecimal b1 = BigDecimal.valueOf(v1);
BigDecimal b2 = BigDecimal.valueOf(v2);
return b1.multiply(b2).doubleValue();
}
/**
* Provide (relatively) accurate division operation. When there is inexhaustible division, it is accurate to
* 10 digits after the decimal point, and the subsequent figures are rounded.
*
* @param v1 Divisor
* @param v2 Divisor
* @return Quotient of two parameters
*/
public static double divide(double v1, double v2) {
return divide(v1, v2, DEF_DIV_SCALE);
}
/**
* Provides (relatively) accurate division. In case of inexhaustible division, it is specified by the scale parameter
* Determine the accuracy, and the subsequent figures are rounded.
*
* @param v1 Divisor
* @param v2 Divisor
* @param scale Indicates that it needs to be accurate to several decimal places.
* @return Quotient of two parameters
*/
public static double divide(double v1, double v2, int scale) {
if (scale < 0) {
throw new IllegalArgumentException(
"The scale must be a positive integer or zero");
}
BigDecimal b1 = BigDecimal.valueOf(v1);
BigDecimal b2 = BigDecimal.valueOf(v2);
return b1.divide(b2, scale, RoundingMode.HALF_UP).doubleValue();
}
/**
* Provide accurate rounding of decimal places.
*
* @param v Number to be rounded
* @param scale How many decimal places are reserved
* @return Rounded results
*/
public static double round(double v, int scale) {
if (scale < 0) {
throw new IllegalArgumentException(
"The scale must be a positive integer or zero");
}
BigDecimal b = BigDecimal.valueOf(v);
BigDecimal one = new BigDecimal("1");
return b.divide(one, scale, RoundingMode.HALF_UP).doubleValue();
}
/**
* Provide precise type conversion (Float)
*
* @param v Number to be converted
* @return Return conversion result
*/
public static float convertToFloat(double v) {
BigDecimal b = new BigDecimal(v);
return b.floatValue();
}
/**
* Provide exact type conversion (Int) without rounding
*
* @param v Number to be converted
* @return Return conversion result
*/
public static int convertsToInt(double v) {
BigDecimal b = new BigDecimal(v);
return b.intValue();
}
/**
* Provide precise type conversion (Long)
*
* @param v Number to be converted
* @return Return conversion result
*/
public static long convertsToLong(double v) {
BigDecimal b = new BigDecimal(v);
return b.longValue();
}
/**
* Returns the larger of two numbers
*
* @param v1 The first number to be compared
* @param v2 The second number to be compared
* @return Returns the larger of two numbers
*/
public static double returnMax(double v1, double v2) {
BigDecimal b1 = new BigDecimal(v1);
BigDecimal b2 = new BigDecimal(v2);
return b1.max(b2).doubleValue();
}
/**
* Returns the smallest of two numbers
*
* @param v1 The first number to be compared
* @param v2 The second number to be compared
* @return Returns the smallest of two numbers
*/
public static double returnMin(double v1, double v2) {
BigDecimal b1 = new BigDecimal(v1);
BigDecimal b2 = new BigDecimal(v2);
return b1.min(b2).doubleValue();
}
/**
* Accurately compare two numbers
*
* @param v1 The first number to be compared
* @param v2 The second number to be compared
* @return If the two numbers are the same, it returns 0. If the first number is larger than the second number, it returns 1. Otherwise, it returns - 1
*/
public static int compareTo(double v1, double v2) {
BigDecimal b1 = BigDecimal.valueOf(v1);
BigDecimal b2 = BigDecimal.valueOf(v2);
return b1.compareTo(b2);
}
}
summary
Floating point numbers cannot be accurately represented in binary, so there is a risk of precision loss.
However, Java provides BigDecimal to manipulate floating-point numbers. The implementation of BigDecimal uses BigInteger (used to operate large integers). The difference is that BigDecimal adds the concept of decimal places.