I'm a sophomore. The purpose of writing this article is to make a certain record of my knowledge and technology, and I'm willing to share it with you. Because I'm still young, there are inevitably some mistakes and omissions in the published article. Please forgive me and correct me if you read this article. If you have any questions during reading, you can also ask them through comments. I will answer the questions according to my ability.
preface
In the last article Binary search tree of data structure and algorithm (Java implementation) In, we discuss the binary search tree, and point out the disadvantages of the binary search tree: when the data is orderly, the structure of the binary search tree will degenerate into a linked list structure. Today, we will discuss the data structure to solve this problem - binary balanced tree AVL tree.

01 - what is AVL tree
The AVL tree is named after the abbreviations of the names of the two inventors of the structure (Adelson velsky and E.M. Landis).
AVL tree inherits the basic characteristics of binary search tree: the left child node is less than the parent node, and the parent node is less than or equal to the right child node. However, different from binary search tree, AVL tree adds a new feature: the height difference of two subtrees of any node can only be one layer at most!
02 - standard AVL tree diagram
The following figure shows a standard AVL tree:
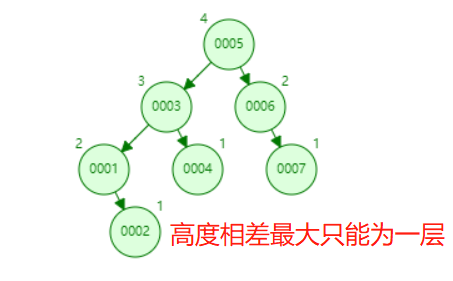
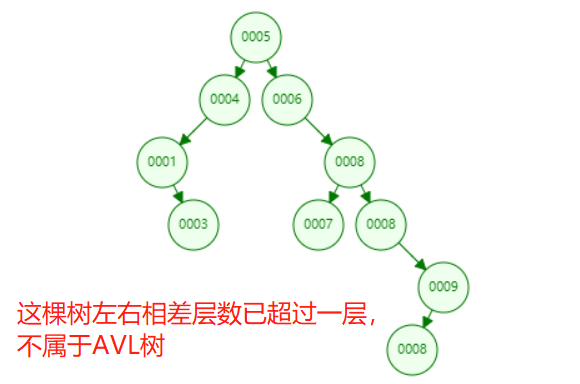
The following figure shows the tree that does not comply with AVL rules:
03 - four cases corresponding to rotation
After understanding the rules of AVL, we need to start thinking: when the inserted data will destroy the rules that the AVL height cannot differ by more than one layer, what operations should be carried out to make the structure follow the rules again. In order to follow the rules, we need to introduce the idea of rotation!
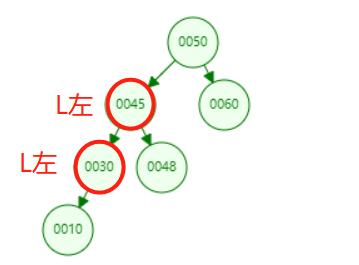
When the AVL rule is broken and out of balance, it can be divided into four situations: LL (left and right), LR (left and right), RR (right and right), Rl (right and left).
LL (left) condition:
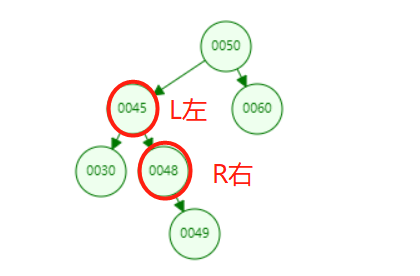
LR (left and right):
RR (right) case:
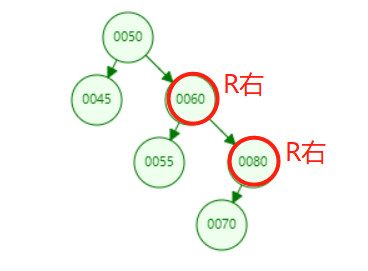
RL (right and left):
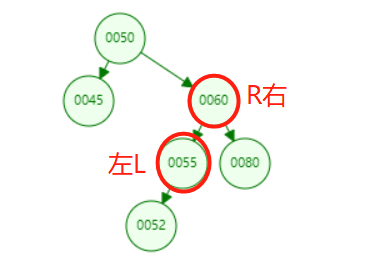
04 - rotation of LL
LL rotation diagram:
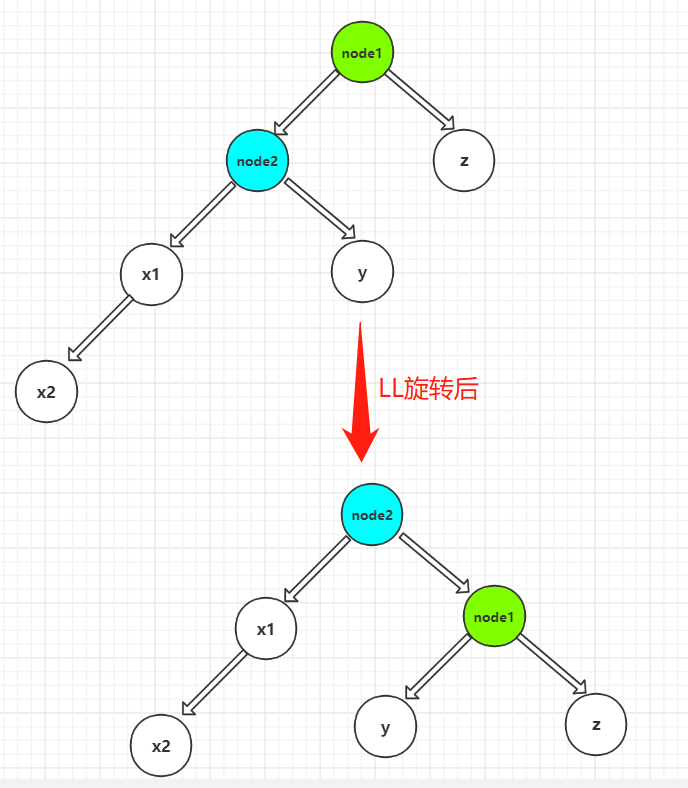
LL rotation: find the parent node of the node that breaks the ring rule, and exchange the parent-child bits between the parent node and the parent node, and the corresponding child node also needs to be replaced. As shown in the figure above: to find the parent node x1 of the node with broken ring rules, the parent node node2 of x1 needs to be exchanged with the parent node node1. In the process of exchange, node2 needs to disconnect the original right child node y from node1, and the left child node of node1 disconnects node2. At this time, the left child node of node1 is empty, The original right child node of node2 needs to be connected with the left child node y of node1.
05 - rotation of RR
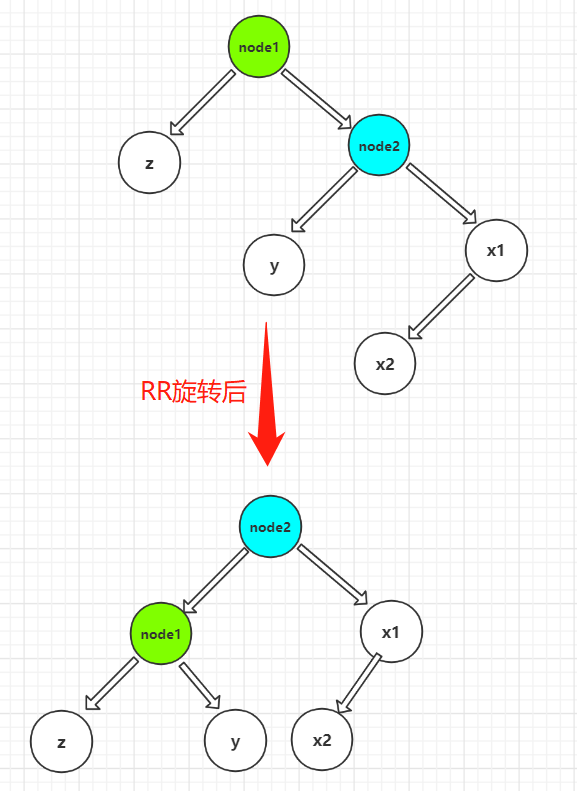
RR rotation: the idea of RR rotation and LL rotation is the same. Find the parent node of the node that breaks the ring rule, exchange the parent-child bits between its parent node and the parent node, and the corresponding child node also needs to be replaced. As shown in the figure above: to find the parent node x1 of the node with broken ring rules, the parent node node2 of x1 needs to be exchanged with the parent node node1. In the process of exchange, node2 needs to disconnect the original left child node y from node1, and the right child node of node1 disconnects node2. At this time, the right child node of node1 is empty, The original right child node of node2 needs to be connected with the left child node y of node1.
06 - rotation of LR
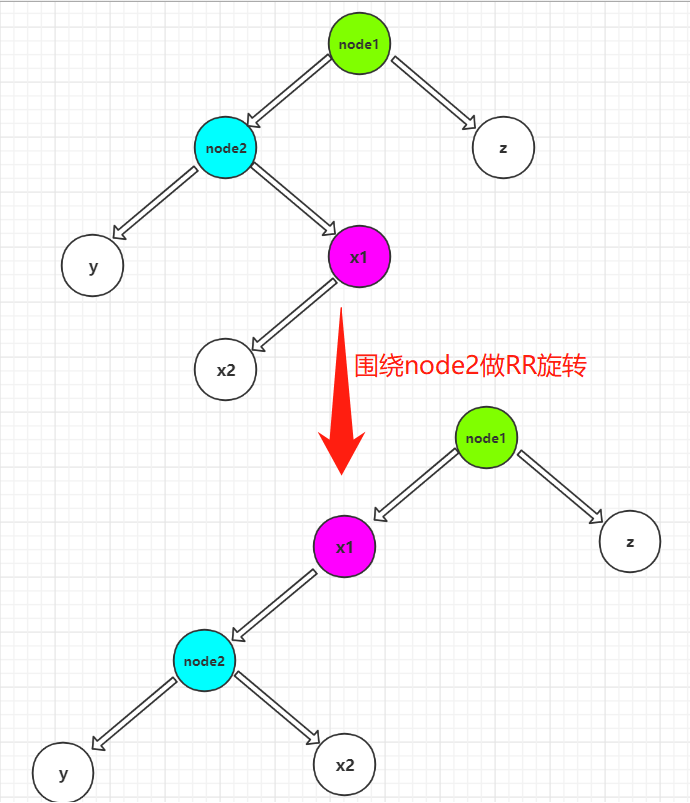
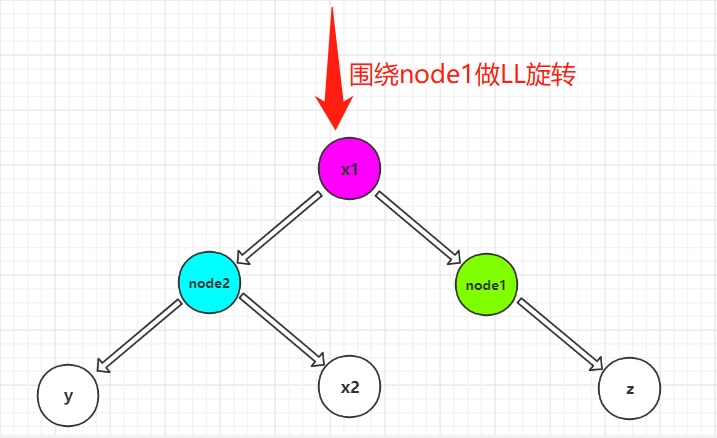
LR rotation: LR rotation is more complex than LL and RR. LR needs to rotate twice, one RR and one LL respectively. As shown in the figure above: first rotate RR around node2, and then rotate LL around node1.
07 - rotation of RL
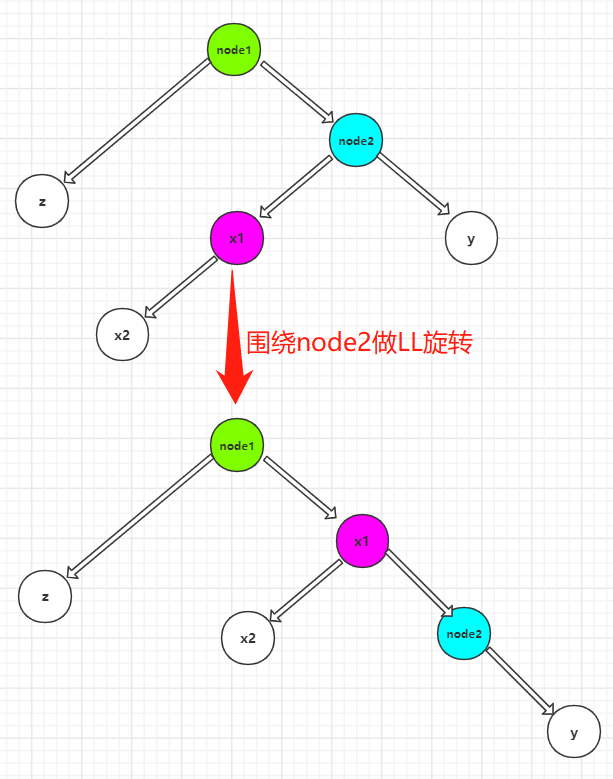
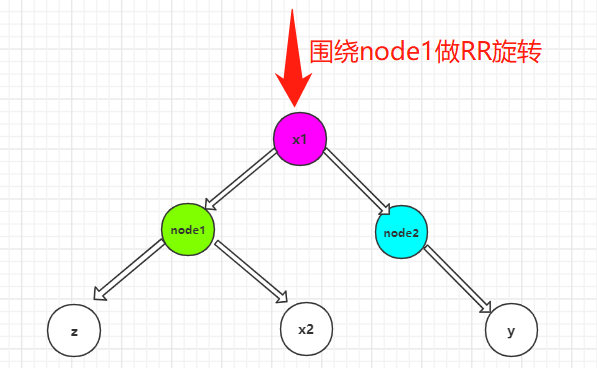
RL rotation: RL rotation is more complex than RR and LL. RL needs to rotate twice, one for ll and one for RR. As shown in the figure above: first rotate ll around node2, and then rotate RR around node1.
So far, we have described and demonstrated the four rotation situations of AVL. Next, we will use code to realize specific functions.
08 - specific code
Node class of tree java
package com.bosen.www;
/**
* <p>Node class</p>
* @author Bosen 2021/6/10 22:01
*/
public class Node {
public Node left; // Left node
public int data; // data
public Node right; // Right node
public Node(Node left, int data, Node right) {
this.left = left;
this.data = data;
this.right = right;
}
}
AVL tree implementation class AVLTree java
package com.bosen.www;
/**
* <p>AVL Tree</p>
* @author Bosen 2021/6/10 22:07
*/
public class AVLTree {
public Node root; // Root node
/*
* Insert operation (recursive implementation)
*/
public void insert(int data) {
root = insert(root, data);
}
public Node insert(Node subNode, int data) {
if (subNode == null) {
return new Node(null, data, null);
}
if (data < subNode.data) {
// Insert into left subtree
subNode.left = insert(subNode.left, data);
if (unbalance(subNode)) {
// The rules are broken
if (data < subNode.left.data) {
subNode = ll(subNode); // LL
} else {
subNode = lr(subNode); // LR
}
}
} else {
// Insert into right subtree
subNode.right = insert(subNode.right, data);
if(unbalance(subNode)) {
// The rules are broken
if (data < subNode.right.data) {
subNode = rr(subNode); // RR
} else {
subNode = rl(subNode); // RL
}
}
}
return subNode;
}
/*
* Delete operation
*/
public void delete(int data) {
root = delete(root, data);
}
public Node delete(Node subNode, int data) {
if (data < subNode.data) {
// The node to be deleted is in the left subtree
subNode.left = delete(subNode.left, data);
} else if (data > subNode.data){
// The node to be deleted is in the right subtree
subNode.right = delete(subNode.right, data);
} else {
// This node is a node that needs to be deleted
if (subNode.left != null && subNode.right != null) {
// Both left and right subtrees exist
if (getDepth(subNode.left, 1) > getDepth(subNode.right, 1)) {
// The height of the left subtree is higher than that of the right subtree
Node max = getMaxNode(subNode.left);
subNode.data = max.data;
subNode.left = delete(subNode.left, max.data);
} else {
// The height of the right subtree is higher than that of the left subtree
Node min = getMaxNode(subNode.right);
subNode.data = min.data;
subNode.right = delete(subNode.right, min.data);
}
} else {
subNode = subNode.left != null ? subNode.left : subNode.right;
}
}
return subNode;
}
/*
* LL
*/
public Node ll(Node node1) {
Node node2 = node1.left;
node1.left = node2.right;
node2.right = node1;
return node2;
}
/*
* RR
*/
public Node rr(Node node1) {
Node node2 = node1.right;
node1.right = node2.left;
node2.left = node1;
return node2;
}
/*
* Lr
*/
public Node lr(Node node1) {
node1.left = rr(node1.left);
return ll(node1);
}
/*
* rl
*/
public Node rl(Node node1) {
node1.right = ll(node1.right);
return rr(node1);
}
/*
* Middle order traversal
*/
public void traverse(Node root) {
if (root != null) {
traverse(root.left);
System.out.print(root.data+"\t");
traverse(root.right);
}
}
/*
* Judge the depth of the tree
*/
public int getDepth(Node root, int deep) {
if (root == null) {
return deep;
}
int leftDeep = deep;
int rightDeep = deep;
if (root.left != null) {
leftDeep = getDepth(root.left, deep+1);
}
if (root.right != null) {
rightDeep = getDepth(root.right, deep+1);
}
return Math.max(leftDeep, rightDeep);
}
/*
* Judge whether the rules are broken
*/
public boolean unbalance(Node root) {
int leftHeight = getDepth(root.left, 1);
int rightHeight = getDepth(root.right, 1);
return Math.abs(leftHeight - rightHeight) > 1;
}
/*
* Get maximum node
*/
public Node getMaxNode(Node node) {
if (node == null) {
return null;
}
if (node.right != null) {
return getMaxNode(node.right);
} else {
return node;
}
}
/*
* Get minimum node
*/
private Node getMinNode(Node node) {
if (node == null) {
return null;
}
if (node.left != null) {
return getMinNode(node.left);
} else {
return node;
}
}
}
👇 Scan QR code attention
