▄█▔▉●
Bisection template
Template 1
int BinarySearch1(vector<int>& nums, int target) {
int l = 0, r = nums.size() - 1;
while (l <= r) {//
int mid = l + (r - l) / 2;
if (nums[mid] == target) {//
return mid;
} else if (nums[mid] > target) {
r = mid - 1;
} else {
l = mid + 1;
}
}
return -1;
}
Template 2
int BinarySearch2(vector<int>& nums, int target) {
int l = 0, r = nums.size() - 1;
while (l < r) {//
int mid = l + (r - l) / 2;
if (nums[mid] >= target) r = mid;//
else l = mid + 1;
}
if (nums[l] == target) return l;
else return -1;
}
int BinarySearch2(vector<int>& nums, int target) {
int l = 0, r = nums.size() - 1;
while (l < r) {
int mid = l + (r - l + 1) / 2;
if (nums[mid] <= target) l = mid;
else r = mid - 1;
}
if (nums[l] == target) return l;
else return -1;
}
Template 3
int BinarySearch3(vector<int>& nums, int target) {
int l = 0, r = nums.size() - 1;
while (l + 1 < r) {
int mid = l + (r - l) / 2;
if (nums[mid] == target) {
return mid;
} else if (nums[mid] > target){
r = mid;
} else {
l = mid;
}
}
if (nums[l] == target) return l;
if (nums[r] == target) return r;
return -1;
}
Time to use dichotomy
When you need to find a number in a range, and this number satisfies the property that the whole array can be divided into two segments without duplication and leakage, you can use bisection.
Key points:
1. The answer to the question needs to be a number
2. It is necessary to find the number in an overall order or local order
3. The basis for the division of the requirements of one topic has two paragraphs
Summary: to put it bluntly, binary search is just because the array itself meets the special property of order, so it is a little more efficient than sequential search. Therefore, when thinking about binary search, you can first think about whether the violent solution can be solved, and then use binary search to improve the efficiency.
Binary subscript series
Search insertion location
Dichotomy
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
// Because the final result of the exclusion method is in the range of [0, num.size() - 1]
// Therefore, if the target is to be inserted at the end of the array, it needs special judgment
if (target > nums.back()) return nums.size();
int l = 0, r = nums.size() - 1;
while (l < r) {
int mid = l + r >> 1;
if (nums[mid] >= target) r = mid;
else l = mid + 1;
}
return l;
}
};
Finds the first and last positions of elements in a sorted array
(two points)
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
if (nums.empty()) return {-1, -1};
// Bisect the first position of the same element
int l = 0, r = nums.size() - 1;
while (l < r) {
int mid = l + r >> 1;
if (nums[mid] >= target) r = mid;
else l = mid + 1;
}
if (nums[l] != target) return {-1, -1};
int first = l;
// Bisect the last position of the same element
l = 0, r = nums.size() - 1;
while (l < r) {
int mid = l + r + 1>> 1;
if (nums[mid] <= target) l = mid;
else r = mid - 1;
}
int second = l;
return {first, second};
}
};
Find the smallest value in the rotation sort array
(two points)
class Solution {
public:
int findMin(vector<int>& nums) {
if (nums.back() > nums.front()) return nums[0];
// Divide the first number less than nums[0]
int l = 0, r = nums.size() - 1;
while (l < r) {
int mid = l + r >> 1;
if (nums[mid] > nums.back()) l = mid + 1;
else r = mid;
}
return nums[l];
}
};
Find the minimum value II in the rotation sort array
(two points)
class Solution {
public:
int findMin(vector<int>& nums) {
while (nums[0] == nums.back() && nums.size() > 1) nums.pop_back();
if (nums.back() > nums[0]) return nums[0];
int target = nums[0];// If you select num [0] as the target, you need to judge whether the whole array is ordered
int l = 0, r = nums.size() - 1;
while (l < r) {
int mid = l + r >> 1;
if (nums[mid] < target) r = mid;
else l = mid + 1;
}
return nums[l];
}
};
Search rotation sort array
(plain dichotomy)
Question: how can an unordered array be solved by bisection?
A completely unordered array cannot be solved by dichotomy, but the unordered array of this problem becomes unordered only after rotating an ordered array, so the unordered array is still relatively ordered locally. Therefore, we can grasp the turning point of rotation, so that the unordered array is divided into two ordered small arrays, so that we can use dichotomy.
Question: how to find the turning point?
Grasp the characteristics of the turning point. If the array is not the original array after rotation, the maximum and minimum values should be respectively on the left and right of the turning point, and the minimum value can be found in a rotation array, so the turning point is found.
Solution: find a turning point in an array, and then find target in two locally ordered arrays.
class Solution {
public:
// Because of the minimum value of dichotomy, you need to find the first value of < = target
// The binary answer needs to find the first value of > = target, so you need to write two binary answers
int BinarySearch(vector<int>& nums, int target, int start, int end) {
int l = start, r = end;
while (l < r) {
int mid = l + r >> 1;
if (nums[mid] >= target) r = mid;
else l = mid + 1;
}
if (nums[l] == target) return l;
else return -1;
}
int search(vector<int>& nums, int target) {
// Find the subscript of the minimum value, which is also the dividing point of the ordered array at both ends
int l = 0, r = nums.size() - 1;
while (l < r) {
int mid = l + r >> 1;
if (nums[mid] <= nums.back()) r = mid;
else l = mid + 1;
}
// Bisect the ordered array at both ends, and then find the answer
int pos = l;
int leftAns = BinarySearch(nums, target, 0, pos - 1);
int RightAns = BinarySearch(nums, target, pos, nums.size() - 1);
return leftAns == -1 ? RightAns == -1 ? -1 : RightAns : leftAns;
}
};
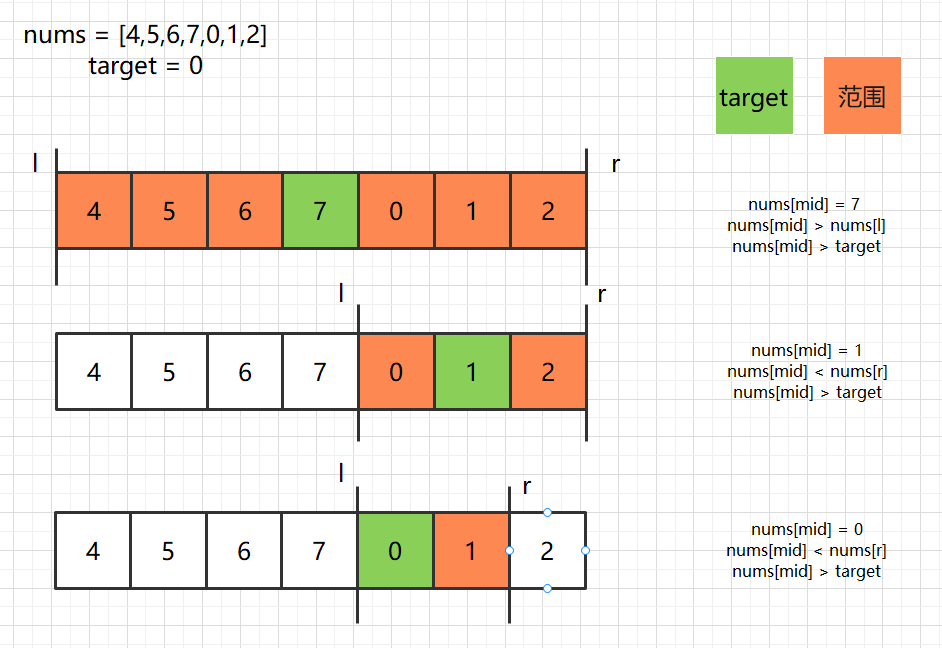
(Rough dichotomy)
The second method, like the first method, carefully finds a turning point and then starts to score two points. This method is rough, but it is also faster.
The first method is to find the turning point, and then dichotomy. In fact, there is no need to find the turning point, because the array has only two segments at most, so any array will fall on an orderly array.
Solution: first, compare num [mid] with num [l] and num [r] to find out that num [mid] is on an ordered array. Then compare with the target to range r or L.
class Solution {
public:
int search(vector<int>& nums, int target) {
int l = 0, r = nums.size() - 1;
while (l <= r) {
int mid = l + r >> 1;
if (nums[mid] == target) return mid;
// The first half of the array is ordered
if (nums[mid] >= nums[l]) {
// target in [l, mid)
if (nums[mid] > target && target >= nums[l]) r = mid - 1;
else l = mid + 1;
}
// The second half of the array is ordered
if (nums[mid] <= nums[r]) {
// target in (mid, r]
if (nums[mid] < target && target <= nums[r]) l = mid + 1;
else r = mid - 1;
}
}
return -1;
}
};
Search rotation sort array ll
What's the difference between this question and the previous one?
The difference is that in this problem, the array is an array whose numbers are arranged in non descending order, and the values in the array may have the same numbers. This destroys the dichotomy of dichotomy.
What is dyadic? That is, you can divide the array so that the numbers in the first half are > num Back(), the numbers in the second half are < = num Back(), so you can find the turning point of the rotating array, then divide the array into two ordered arrays, and finally bisect the two ordered arrays to find the target.
Unfortunately, if the same number appears in the array, you may be looking for a turning point in the rotation array, and the number in the first half of the array is > = num Back(), the number in the second half array is also < = num Back(), if you can't divide the array into two sections, you can't use bisection to find the turning point of rotating the array.
So as long as you delete one end of the same number at the beginning and end of the array, you can distinguish the first and second arrays. So while (num.size() > 1 & & num back() == nums[0]) nums. pop_ back(); Just delete the same numbers.
The following two versions add while (num.size() > 1 & & num back() == nums[0]) nums. pop_ back(); That's it.
(two points)
class Solution {
public:
bool BinarySearch(vector<int>& nums, int l, int r, int target) {
while (l < r) {
int mid = l + r >> 1;
if (nums[mid] >= target) r = mid;
else l = mid + 1;
}
return nums[l] == target;
}
bool search(vector<int>& nums, int target) {
while (nums.size() > 1 && nums.back() == nums[0]) nums.pop_back();
// Found < = num First number of back()
int l = 0, r = nums.size() - 1;
while (l < r) {
int mid = l + r >> 1;
if (nums[mid] <= nums.back()) r = mid;
else l = mid + 1;
}
int pos = l;
// Search for the existence of target in two ordered arrays
bool flag1 = BinarySearch(nums, 0, pos - 1, target) ;
bool flag2 = BinarySearch(nums, pos, nums.size() - 1, target);
return flag1 || flag2;
}
};
(Rough dichotomy)
class Solution {
public:
int search(vector<int>& nums, int target) {
while (nums.size() > 1 && nums.back() == nums[0]) nums.pop_back();
int l = 0, r = nums.size() - 1;
while (l <= r) {
int mid = l + r >> 1;
if (nums[mid] == target) return true;
// Here is > =, because there is only one number in the first half of the array. If you don't add =, you may miss the answer
// The first half of the array is ordered
if (nums[mid] >= nums[l]) {
// target in [l, mid)
if (nums[mid] > target && target >= nums[l]) r = mid - 1;
else l = mid + 1;
} else {// The second half of the array is ordered
// target in (mid, r]
if (nums[mid] < target && target <= nums[r]) l = mid + 1;
else r = mid - 1;
}
}
return false;
}
};
First wrong version
Obviously, we can divide the numbers in the array into two paragraphs. The first paragraph is all true and the last paragraph is all false. Therefore, we can think of using dichotomy from the nature of dichotomy.
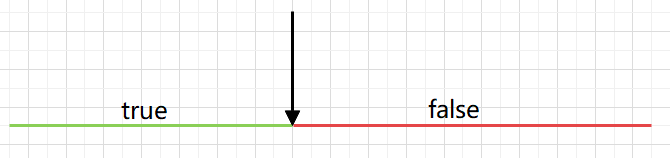
There are two versions of dichotomy. The first is to find the first false, and the second is to find the last true and then + 1.
(two points)
class Solution {
public:
int firstBadVersion(int n) {
int l = 1, r = n;
while (l < r) {
int mid = l + (r - l) / 2;
if (isBadVersion(mid)) r = mid;// If correct, narrow the range forward
else l = mid + 1;
}
return l;
}
};
(two points)
class Solution {
public:
int firstBadVersion(int n) {
int l = 1, r = n;
while (l < r) {
int mid = l + (r - l + 1) / 2;
if(!isBadVersion(mid)) l = mid;
else r = mid - 1;
}
// Prevent the special case of n = 1 and bad = 1 from entering the cycle. So we need a special judgment
return !isBadVersion(r) ? r + 1 : r;
}
};
Peak index of mountain range array
(violence)
The first method is violence, traversing from front to back. When num [mid] < num [mid + 1] continues, when num [mid] > num [mid + 1] stops.
(two points)
Since you want to find a number in the array and the array is divided into two segments, you need to consider whether bisection can be used. Before using bisection, you need to consider whether the number in the array has bisection.

Because many of the previous binary topics have a target or a reference number, and then take this number as the benchmark, and then divide the array into two segments.
However, it seems that there is no ready-made reference number for this topic, but it should not be limited to the thinking that we must find a fixed reference number, because the duality only requires a property that can exactly divide the array into two segments. After careful observation, it is not difficult to find that the first half of the array is increasing, and the second half of the array is decreasing, which divides the array into two segments.
So there are two dichotomies according to this point. The first is to find the index of the first number that begins to decline.
class Solution {
public:
int peakIndexInMountainArray(vector<int>& nums) {
int l = 0, r = nums.size() - 2;
while (l < r) {
int mid = l + r >> 1;
if (nums[mid] > nums[mid + 1]) r = mid;
else l = mid + 1;
}
return l;
}
};
(two points)
The second is to find the index of the last increasing number.
class Solution {
public:
int peakIndexInMountainArray(vector<int>& nums) {
// Because nums Size () > = 3, so don't worry about not entering while
int l = 0, r = nums.size() - 2;
while (l < r) {
int mid = l + r + 1 >> 1;
if (nums[mid] < nums[mid + 1]) l = mid;
else r = mid - 1;
}
return l + 1;
}
};
(three points)
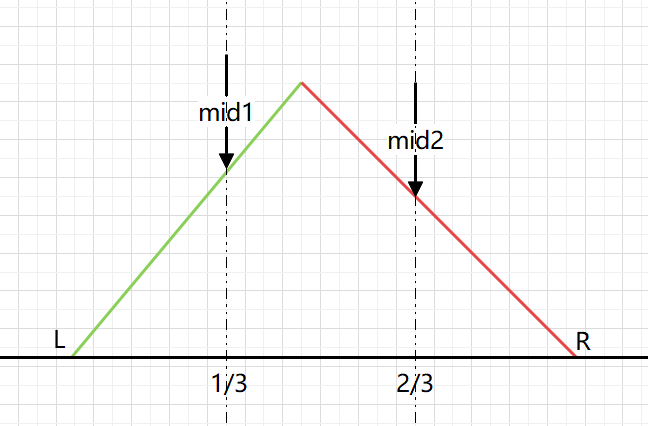
There is another way: three points. The general trisection problem can solve the single peak problem.
Three points: divide the array into three segments, and then send a 1 / 3 interval each time, and finally approach the peak.
Specific method: divide the interval into [L, mid1], [mid1, mid2], [mid2, R]. If arr [mid1] > nums [mid2], it means that the peak must not be in the [mid2, R] interval, so R = mid2 - 1. Similarly, if arr [mid2] > arr [mid1], the peak must not be in the middle of [L, mid1], L = mid1 + 1.
class Solution {
public:
int peakIndexInMountainArray(vector<int>& arr) {
int l = 0, r = arr.size() - 1;
while (l < r) {
int mid1 = l + (r - l) / 3;
int mid2 = r - (r - l) / 3;
if (arr[mid1] > arr[mid2]) {
r = mid2 - 1;
} else {
l = mid1 + 1;
}
}
return l;
}
};
Find target value in array
(two points)
This question seems very difficult, but it is actually a combination of three questions.
Find target value in mountain array = find peak index + find target in positive array + find target in reverse array
stay Peak index of mountain range array How to find the index of the peak value by using two or three points is explained in detail, and finding the target in the positive array or reverse array is the basic question type of two points.
/**
* // This is the MountainArray's API interface.
* // You should not implement it, or speculate about its implementation
* class MountainArray {
* public:
* int get(int index);
* int length();
* };
*/
class Solution {
public:
int findInMountainArray(int target, MountainArray &mountainArr) {
int l = 0, r = mountainArr.length() - 2;
while (l < r) {
int mid = l + r >> 1;
if (mountainArr.get(mid) > mountainArr.get(mid + 1)) r = mid;
else l = mid + 1;
}
int MaxIndex = l;// Peak index
// Looking for target in [0, MaxIndex] of array
l = 0, r = MaxIndex;
while (l < r) {
int mid = l + r >> 1;
if (mountainArr.get(mid) >= target) r = mid;
else l = mid + 1;
}
if (mountainArr.get(l) == target) return l;
// If target is not found in the first half of the array
// Find the target in [MaxIndex+1, mountainArr.length()-1]
l = MaxIndex + 1, r = mountainArr.length() - 1;
while (l < r) {
int mid = l + r >> 1;
if (mountainArr.get(mid) <= target) r = mid;
else l = mid + 1;
}
if (mountainArr.get(l) == target) return l;
else return -1;
}
};
(three points for peak + two points for target)
/**
* // This is the MountainArray's API interface.
* // You should not implement it, or speculate about its implementation
* class MountainArray {
* public:
* int get(int index);
* int length();
* };
*/
class Solution {
public:
int findInMountainArray(int target, MountainArray &mountainArr) {
// Three point index for finding peaks
int l = 0, r = mountainArr.length() - 1;
while (l < r) {
int mid1 = l + (r - l) / 3;
int mid2 = r - (r - l) / 3;
if (mountainArr.get(mid1) > mountainArr.get(mid2)) {
r = mid2 - 1;
} else {
l = mid1 + 1;
}
}
int MaxIndex = l;// Peak index
// Looking for target in [0, MaxIndex] of array
l = 0, r = MaxIndex;
while (l < r) {
int mid = l + r >> 1;
if (mountainArr.get(mid) >= target) r = mid;
else l = mid + 1;
}
if (mountainArr.get(l) == target) return l;
// If target is not found in the first half of the array
// Find the target in [MaxIndex+1, mountainArr.length()-1]
l = MaxIndex + 1, r = mountainArr.length() - 1;
while (l < r) {
int mid = l + r >> 1;
if (mountainArr.get(mid) <= target) r = mid;
else l = mid + 1;
}
if (mountainArr.get(l) == target) return l;
else return -1;
}
};
Binary answer series
Square root of x
(two points)
The square root of a number x must be between [0, x]. When you see looking for a value in an ordered range, you can think of dichotomy. However, whether bisection can be used to find a target value needs to judge whether the logic of finding this value can divide the number in the whole range into two segments. That is, whether it has two stages.
It is not difficult to find that the squares of all numbers in this range are either > x, or < x, or = = X. So this can take all the numbers into account without repetition and leakage, so you can use bisection. Although the previous sentence looks like nonsense, you can also use this idea to judge whether you can use binary decomposition next time you encounter a more difficult problem.
class Solution {
public:
int mySqrt(int x) {
if (x == 0 || x == 1) return x;// If it is 0 or 1, it returns x directly
uint64_t l = 0, r = x / 2;
while (l < r) {
int mid = l + (r - l + 1) / 2;
if (mid <= x / mid) l = mid;
else r = mid - 1;
}
return l;
}
};
The cubic root of a number
(floating point binary)
The above topic is integer dichotomy. This topic is a floating-point dichotomy, which is to find a floating-point number in a range.
In fact, logic is similar to integer dichotomy. However, it should be noted that the price comparison of floating-point numbers cannot be the same as integer comparison. It is very clear to use = = to compare the equality of two numbers.
Because of the storage of floating-point numbers, they can never be equal in precision 0. Therefore, when two numbers are less than a very small number (such as 1e-6), it is determined that the two numbers are equal.
Floating point number bisection is not only special when comparing two numbers, but also special when delimiting the range. In integer bisection, because the downward rounding of division may have multiple identical numbers in the array, the boundary of bisection needs to be controlled. However, there is no need to consider so much in binary floating-point numbers. Judge directly, and then either l = mid or r = mid. Because there is only one floating-point number in a number, and the division of floating-point numbers is not rounded down.
Summary: when the floating-point number is divided into two parts, first, you need to take a small number as a reference when comparing the two numbers. Second, when narrowing the scope, there is no need to consider the boundary.
#include <iostream>
using namespace std;
#define eps 1e-6
int main()
{
double x;
cin >> x;
double l = -1000, r = 1000;
while ((r - l) >= eps) {
double mid = (r + l) / 2.0;
if (mid * mid * mid <= x) l = mid;
else r = mid;
}
printf("%.6f\n", l);
return 0;
}
Find duplicates
(violence)
Violence is to compare all the numbers in pairs, and if a duplicate number is found in the middle, it will be returned directly.
The violent method does not use the feature that all the numbers in the array are between [1, n], so it is the most useful but also the slowest.
class Solution {
public:
int findDuplicate(vector<int>& nums) {
for (int i = 0; i < nums.size(); i ++) {
int num = nums[i];
for (int j = i + 1; j < nums.size(); j ++) {
if (num == nums[j]) return num;
}
}
return 0;
}
};
-
Time complexity O(N2)
-
Space complexity O(1)
(hash mapping)
Because the n+1 numbers in the array are all between [1, n], it should be a radish and a pit, but now there are two radishes in a pit. First, find the extra radish.
In this way, it is not difficult to think of using a hash table to map each number to a position in the array. Following this idea, you can traverse the array, and then map the numbers to the corresponding position in the array. If there are already numbers in the position, you can return the repeated numbers. (you can also use unordered_set hash table).
class Solution {
public:
int findDuplicate(vector<int>& nums) {
int n = nums.size();
vector<int> cnt(n + 1, 0);
// Place num [i] in position num [i]
// If a position is placed twice, it means that the number is a duplicate number
for (int i = 0; i < nums.size(); i ++) {
if (cnt[nums[i]] != 0) return nums[i];
cnt[nums[i]] = nums[i];
}
return 0;
}
};
- Time complexity O(N)
- Space complexity O(N)
(sort)
Since it is a duplicate number, the two duplicate numbers will be next to each other after sorting. So as long as the sequence is finished, finding the adjacent and equal elements is the repeated elements.
The sorting algorithm does not use the property that the numbers in the array are between [1, n].
class Solution {
public:
int findDuplicate(vector<int>& nums) {
sort(nums.begin(), nums.end());
for (int i = 0; i < nums.size() - 1; i ++) {
if (nums[i + 1] == nums[i]) return nums[i];
}
return 0;
}
};
- Time complexity O(Nlogn)
- Space complexity O(1)
(two points)
According to the drawer principle: put 11 apples in 10 drawers, then there are at least 2 apples in one drawer.
There is a number m in the range of [1, n]. If the number of < = M = = m in the array num, the previous number indicates that M is not a duplicate element. However, if the number of < = m > m in the array num, it means that M is the number after the repeated element, or m is the repeated number, because the original number = = m, but because m is the repeated element, there will be one more number less than m.
In this way, the number of [1,n] can be divided into two segments (the number before the repeated number = = m, after the heavy number, or the number of repeated numbers > m).

class Solution {
public:
int findDuplicate(vector<int>& nums) {
int l = 1, r = nums.size() - 1;// The search interval is [1, n (i.e. nums.size() - 1)]
while (l < r) {
int mid = l + r >> 1;
// Count the number of < = mid
int cnt = 0;
for (int num : nums) {
if (num <= mid) cnt ++;
}
// narrow the range
if (cnt > mid) r = mid;
else l = mid + 1;
}
return l;
}
};
- Time complexity O(Nlogn)
- Space complexity O(1)
(double pointer)
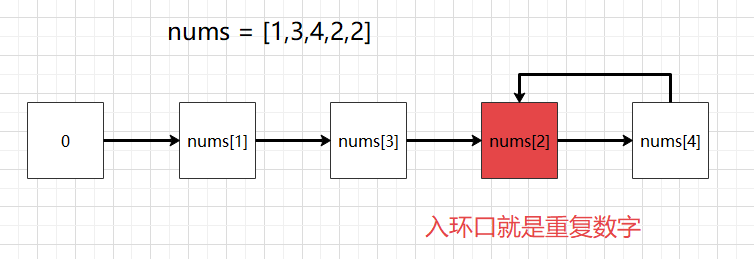
Because the numbers in the array are between [1,n], if there are no duplicate numbers, a linked list will be formed according to the logic of M = num [M], such as num = {1, 2, 3, 4}, forming 1 - > 2 - > 3 - > 4. (it's hard to think of this. You can think of it like this: because there is no same number and no number 0 (within the range of [1,n] starting from 1), it is impossible for the two numbers to point to each other).
If there are duplicate numbers in the array, the two numbers may point to each other, which forms a closed-loop linked list, and the duplicate numbers are the entry of the linked list.
class Solution {
public:
int findDuplicate(vector<int>& nums) {
int fast = 0, slow = 0;
while (1) {
fast = nums[nums[fast]];
slow = nums[slow];
if (slow == fast) break;
}
fast = 0;// Start from scratch
while (slow != fast) {
fast = nums[fast];
slow = nums[slow];
}
return fast;
}
};
- Time complexity O(N)
- Space complexity O(1)
Transform the array closest to the target in the array and
(two points 1)
In fact, this problem is to find a number mid in [0, max(arr[i]) (max(arr[i]) refers to the maximum value in the ARR array). This number can be. All numbers > mid in the array become mid, and finally the sum in the array can be closest to the target.
The difficulty of this problem is to find the number closest to the target, rather than finding a specific integer.
If this problem is changed to find the array and equal to target (guaranteed to have a solution), will you? After this change, it has become a classic dichotomy problem. You can use bisection directly, and then judge the first number that makes the array and > = target in the check() function. Just return.
In fact, writing here is already very close to the answer. Why? Because the number closest to the target must be two. One number can make the array and > = target, and one number can make the array and < = target. So if you find the first number left that can make the array and > = target, the other number that can make the array and the nearest target is left - 1. Finally, compare left and left-1, and take one that can make the array and closer to the target.
class Solution {
public:
int Sum(int mid, vector<int>& arr) {
int sum = 0;
for (int num : arr) sum += min(num, mid);
return sum;
}
int findBestValue(vector<int>& arr, int target) {
int l = 0, r = 0;
for (int n : arr) r = max(r, n);
while (l < r) {
int mid = l + r >> 1;
if (Sum(mid, arr) >= target) r = mid;
else l = mid + 1;
}
int up = Sum(l, arr);
int low = Sum(l - 1, arr);
if (abs(up - target) < abs(target - low)) return l;
else return l - 1;
}
};
(2 points)
Of course, find the first number that makes the array and > = target. You can also find the number right of the last < = target, and then compare right and right + 1, which can make the array and closer to the target.
class Solution {
public:
int Sum(int mid, vector<int>& arr) {
int sum = 0;
for (int i = 0; i < arr.size(); i ++) sum += min(arr[i], mid);
return sum;
}
int findBestValue(vector<int>& arr, int target) {
int l = 0, r = 0;
// //Find maximum r
for (int n : arr) r = max(r, n);
while (l < r) {
int mid = l + r + 1 >> 1;
if (Sum(mid, arr) <= target) l = mid;
else r = mid - 1;
}
int low = Sum(l, arr);
int up = Sum(l + 1, arr);
if (abs(low - target) <= abs(target - up)) return l;
else return l + 1;
}
};
Binary series with complex judgment conditions
Ke Ke, who likes bananas
(two points)
Find a number in a range, which makes the number of times to offset all numbers < = h, and find the minimum value of the number.
This is much like the problem of dichotomy, finding out that a number satisfies a certain property.
Therefore, the first number of time < = h is found by inserting the dichotomy template. Note that this problem is a little windy when solving h, because the smaller the mid, the longer it takes, and the larger the mid, the smaller the month it takes. So when the calculated time < = h, r = mid should narrow the range on the right.
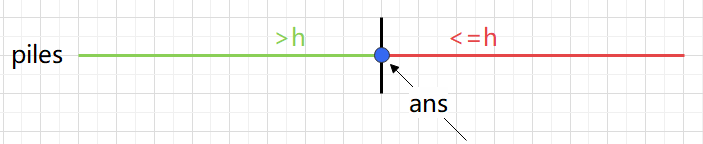
Rounding up tips for division: (a + b - 1) / b
class Solution {
public:
int Hour(int mid, vector<int>& piles) {
int cnt = 0;
for (int n : piles) {
cnt += (n + mid - 1) / mid;// n/mid rounded up
}
return cnt;
}
int minEatingSpeed(vector<int>& piles, int h) {
int l = 1, r = 0;// l starts with 1 because the divisor in division cannot be 0
// Range [1, max(piles[i])]
for (int n : piles) r = max(n, r);
while (l < r) {
int mid = l + r >> 1;
// Find the first number < = H
// The smaller the mid, the greater the time
if (Hour(mid, piles) <= h) r = mid;
else l = mid + 1;
}
return l;
}
};
Maximum value of split array (classic template question: minimize the maximum value)
Non negative integers and continuous subarrays are very important
(dynamic gauge)
class Solution {
public:
int splitArray(vector<int>& nums, int m) {
vector<vector<int>> dp(nums.size() + 1, vector<int>(m + 1, INT_MAX));
// Find the prefix and
vector<int> sum(nums.size() + 1, 0);
for (int i = 1; i <= nums.size(); i ++) sum[i] = nums[i - 1] + sum[i - 1];
dp[0][0] = 0;
for (int i = 1; i <= nums.size(); i ++) {// Array length
for (int j = 1; j <= m; j ++) {// Number of subsets after segmentation
for (int k = 0; k < i; k ++) {
dp[i][j] = min(dp[i][j], max(dp[k][j - 1], sum[i] - sum[k]));
}
}
}
return dp[nums.size()][m];
}
};
(dichotomy + greed)
class Solution {
public:
// When the maximum sum in the array does not exceed maxSum, Num should be divided into several segments
int split(vector<int>& nums, int maxSum) {
int subCnt = 1;// The number of consecutive sets in the array
int curSum = 0;
for (int num : nums) {
if (curSum + num > maxSum) {
subCnt ++;
curSum = 0;
}
curSum += num;
}
return subCnt;
}
int splitArray(vector<int>& nums, int m) {
int l = 0, r = 0;// l is the maximum value in a number, and r is the maximum value in the whole array, that is, the sum of the whole array
int sum = 0;
for (int num : nums) {
l = max(num, l);
sum += num;
}
r = sum;
while (l < r) {
int mid = l + r >> 1;
if (split(nums, mid) <= m) r = mid;
else l = mid + 1;
}
return l;
}
};
Ability to deliver packages within D days
(violence)
First of all, we can think about how to solve the problem of violence?
The requirement is the minimum load capacity required to deliver the package within D days. Focus on the minimum load capacity. Now you might as well estimate what the load capacity can go. If the load capacity in one day is infinite, no matter how many items can be delivered in one day, this is the biggest example. What if it is a little larger than the infinite size? Or within one day. We find that there can be many values to meet the delivery within D days, so we will make a small estimate. If the number of days is not considered, what is the minimum load capacity required to deliver all goods, it is not difficult to find that it is the one with the heaviest load among all goods, because if all goods are to be delivered, each goods cannot be delivered in two, so to ensure the delivery of the heaviest goods, the minimum load capacity is the weight of the heaviest goods.
According to the above analysis, the lowest load capacity is actually [max(weight[i]), but this infinity can also be reduced a little. If all goods are to be delivered in one day, the load capacity is the sum of the weight of all goods. So the load capacity is [max(weights[i]), sum(weights[i])
Because the order of delivery must be in order, that is, the number in the array must be accessed continuously. Therefore, if a load capacity is given, the corresponding delivery days can be calculated.
To sum up: there is a range of total weight capacity, and the corresponding days can also be calculated according to the total weight of delivery. In this way, the corresponding days can be calculated for all load capacity, and then compared with the expected days. If the load capacity is positively enumerated, the first load capacity meeting the delivery days < = days is the lowest load capacity. (days is inversely proportional to the carrying capacity. The stronger the carrying capacity, the smaller the days)
class Solution {
public:
int split(vector<int>& weights, int maxLoad) {
int days = 1;// Delivery takes at least one day
int curLoad = 0;// Current cargo capacity
for (int w : weights) {
if (curLoad + w > maxLoad) {// If > maxload is added to the current number, it indicates that the load has reached the upper limit
days ++;
curLoad = 0;
}
curLoad += w;
}
return days;
}
int shipWithinDays(vector<int>& weights, int days) {
int l = 0, r = 0;
for (int w : weights) {
l = max(l, w);
r += w;
}
for (int i = l; i <= r; i ++) {
if (split(weights, i) <= days) return i;
}
return 0;
}
};
(dichotomy + greed)
Through the analysis of the violence method, we can extract a number from a range of numbers, and find a number that satisfies the number of delivery days < = days.
Therefore, it is not necessary to search in order. You can use two separate methods to solve the problem.
class Solution {
public:
int split(vector<int>& weights, int maxLoad) {
int days = 1;// Delivery takes at least one day
int curLoad = 0;// Current cargo capacity
for (int w : weights) {
if (curLoad + w > maxLoad) {// If > maxload is added to the current number, it indicates that the load has reached the upper limit
curLoad = 0;
days ++;
}
curLoad += w;
}
return days;
}
int shipWithinDays(vector<int>& weights, int days) {
int l = 0, r = 0;
for (int w : weights) {
l = max(l, w);
r += w;
}
while (l < r) {
int mid = l + r >> 1;
if (split(weights, mid) <= days) r = mid;
else l = mid + 1;
}
return l;
}
};
Number of days required to make m bouquets
(two points)
The requirement is to wait at least a few days to pick m bouquets of flowers.
You can know that if m * k < = bloomday, you can pick m bouquets as long as you wait for all the flowers to bloom. Therefore, the waiting days can be determined, which must be in the middle of [0, max (Bloom day [i]).
Therefore, as long as a number is calculated within this range, the continuous k flowers can become a bunch, and then m flowers can be obtained. And this number requirement is a number that can meet the requirement of getting bouquet > = m. You can use two points.
class Solution {
public:
int calcFlowers(vector<int>& bloomDay, int maxDays, int k) {
int cnt = 0;// Number of bouquets
int flowers = 0;// Number of current flowers
for (int day : bloomDay) {
if (day <= maxDays) {
flowers ++;
} else {
flowers = 0;
}
if (flowers == k) {
cnt ++;
flowers = 0;
}
}
return cnt;
}
int minDays(vector<int>& bloomDay, int m, int k) {
if (m * k > bloomDay.size()) return -1;
int l = 1e9, r = 0;// Days elapsed
for (int d : bloomDay) {
l = min(l, d);
r = max(r, d);
}
while (l < r) {
int mid = l + (r - l) / 2;
if (calcFlowers(bloomDay, mid, k) >= m) r = mid;
else l = mid + 1;
}
return l;
}
};
Xiao Zhang's question brushing plan
(dichotomy + greed)
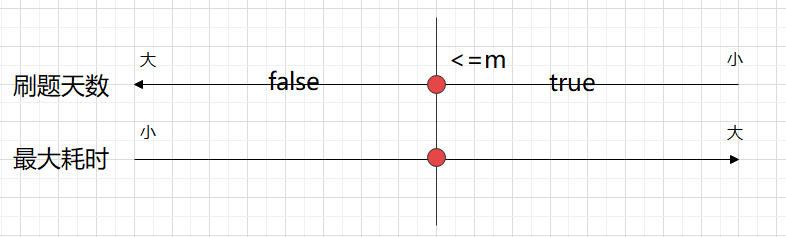
class Solution {
public:
int CalcDays(vector<int>& time, int mid) {
int cnt = 1;
int curSum = 0;// Accumulated time spent on current question brushing
int maxVal = 0;// Record the most time-consuming topics
for (int t : time) {
curSum += t;
maxVal = max(maxVal, t);
if (curSum - maxVal > mid) {
cnt ++;
maxVal = t;
curSum = t;
}
}
return cnt;
}
int minTime(vector<int>& time, int m) {
int l = 0, r = 0;
for (int t : time) {
r += t;
}
while (l < r) {
int mid = l + r >> 1;
if (CalcDays(time, mid) <= m) r = mid;
else l = mid + 1;
}
return l;
}
};
Summary: Minimize Maximum
Suitable topic: 1 Sum of consecutive subarrays 2 Array is a nonnegative integer