Write in front
We talked about the basic concept of tree. This article mainly talks about the basic operations of common trees, such as finding, adding, deleting, etc. It is easier to understand by moving graph.
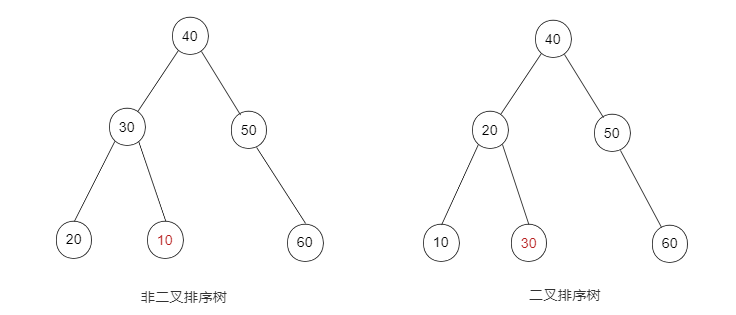
Binary lookup tree
Binary Sort Tree (BST), also known as Binary Sort Tree, or binary search tree. A binary lookup tree satisfies the following conditions:
- All values of the left subtree are less than those of the root node
- All values of the right subtree are greater than those of the root node
- The left and right subtrees also meet the above two points
Generally speaking, it is a binary tree with small nodes on the left and large nodes on the right.
Insert operation
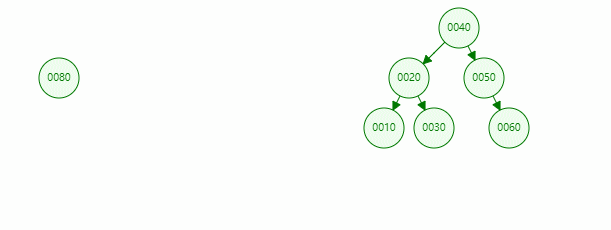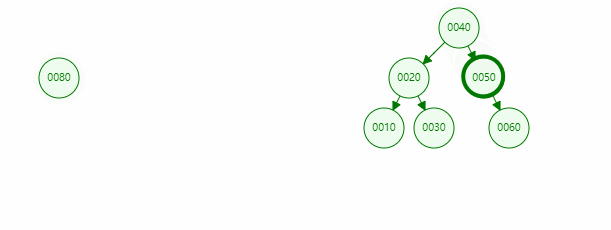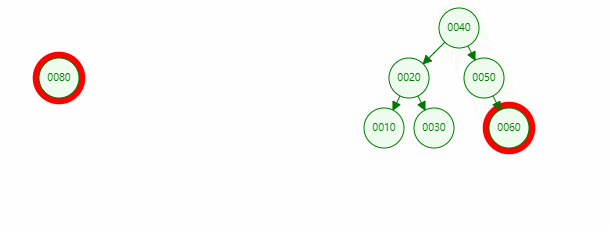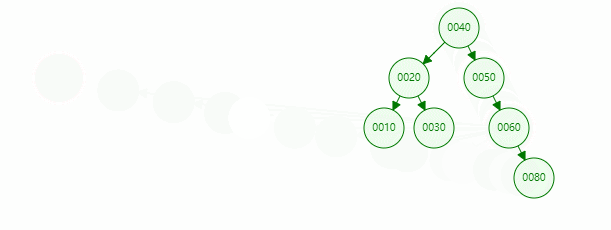
The insertion operation of a binary lookup tree. If the inserted value x starts from the root node:
- If the value of x is less than the value of this node, continue in the left subtree
- If the x value is greater than the node value, continue in the right subtree
- If the node is a leaf node and the X value is less than the node value, the left child node is inserted; otherwise, the right node is inserted
In the binary sort tree above, if the value of the inserted node is 80, the specific operations are as follows:
Find operation
For the search operation of a binary search tree, if the search value x starts from the root node:
- If x is less than the root node, continue searching in the left subtree
- If x is greater than the root node, continue searching in the right subtree
- If the value of x is equal to the root node, the node is returned
- If none can be found, null is returned
In the binary sort tree above, if we need to find a node with a value of 10, the specific operations are as follows:
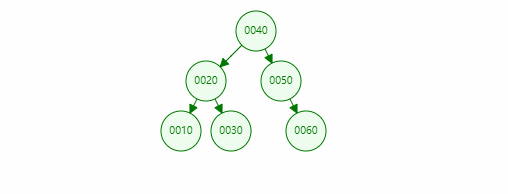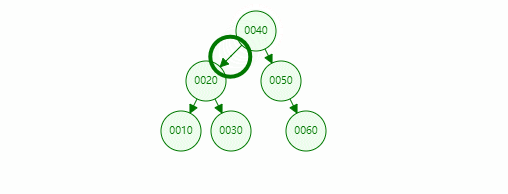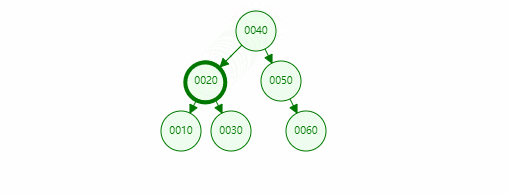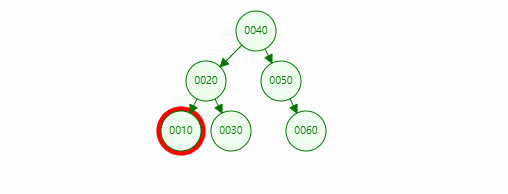
Traversal tree
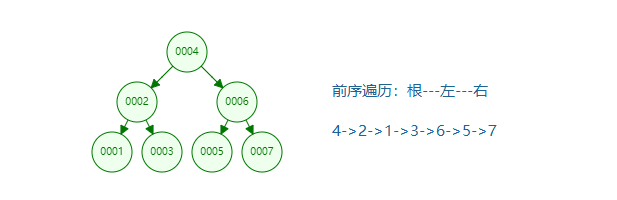
There are three ways to traverse a tree. preorder, inorder, postorder.
Preorder traversal
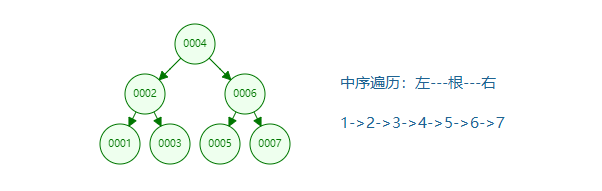
Medium order traversal
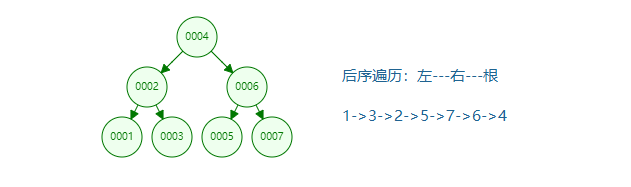
Postorder traversal
Maximum and minimum
Minimum value: find the left child node of the root node and keep looking to the left until the node without left child node is the minimum node
Maximum: find the right child node of the root node and keep looking right until the node without the right child node is the minimum node
Delete operation
This node is a leaf node
When the node is a leaf node, it is deleted directly, and the reference from the parent node to the child node is set to null.
Delete a binary lookup tree. If the deleted value x starts from the root node:
- If the value of the node is equal to x, it is deleted
- If the value of x is less than the value of this node, continue in the left subtree
- If the x value is greater than the node value, continue in the right subtree
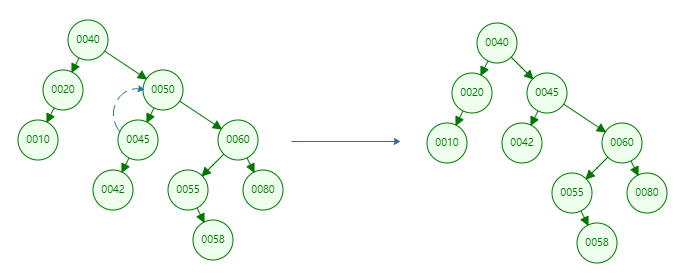
If the value of the deleted node is 80, the specific operations are as follows:
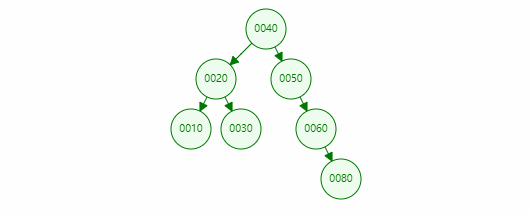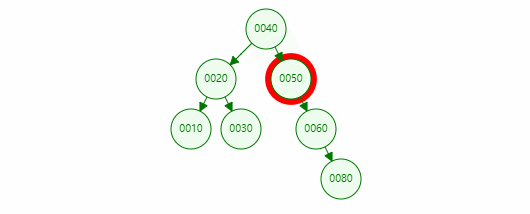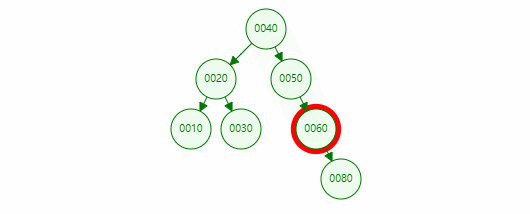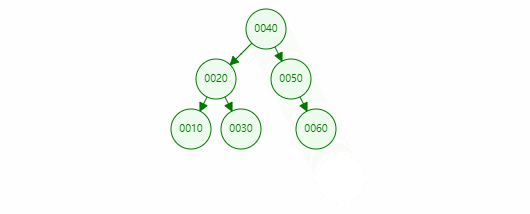
This node has a child node
A node has a child node, which is divided into two cases. Judge whether it is the left child node or the right child node of the parent node, and point the reference of the parent node to the child node of the node (the child node should also be divided into left and right child nodes, equivalent to a total of four cases)
Left: that is, the deleted node is on the left of the root node, the deleted node is on the left of its parent node, and the child node of the deleted node is the left child node
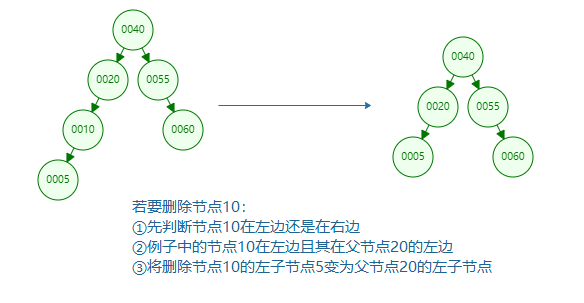
Left, right and left: that is, the deleted node is on the left of the root node, the deleted node is on the right of its parent node, and the child node of the deleted node is the left child node
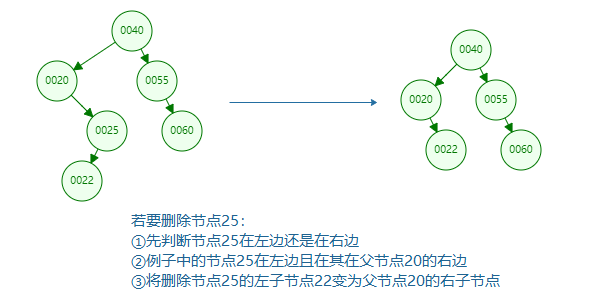
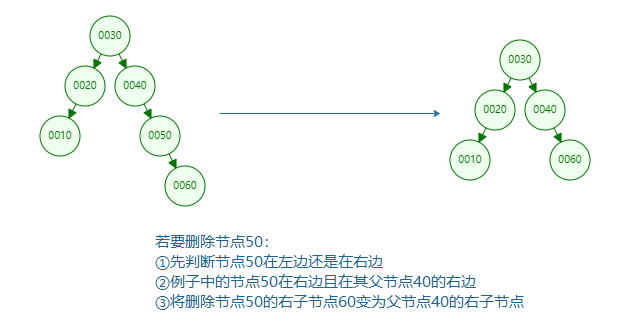
Right: that is, the deleted node is on the right of the root node, the deleted node is on the right of its parent node, and the child node of the deleted node is the right child node
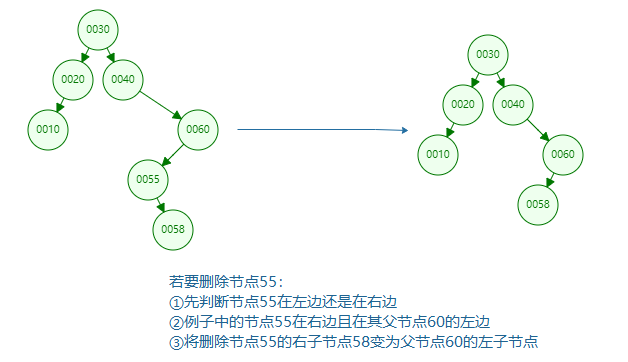
Right, left and right: that is, the deleted node is on the right of the root node, the deleted node is on the left of its parent node, and the child node of the deleted node is the right child node
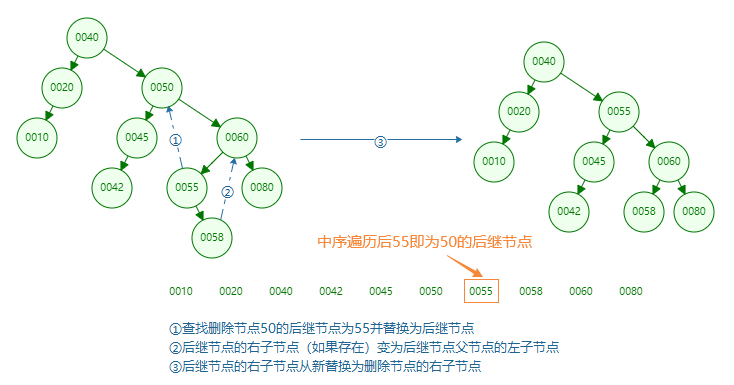
This node has two child nodes
Due to the characteristics of binary search tree, it is ensured that the value of the left subtree of a node is less than that of the node and the value of the right subtree is greater than that of the node. Just find the maximum value in the left subtree or the minimum value in the right subtree (also known as the intermediate successor node) to replace the node, so as to ensure that the subsequent node can be deleted as a binary search tree.
Successor node
In the binary search tree, nodes are arranged in the way of small on the left and large on the right. For any node, the node with the second higher value than the node is its middle successor, which is called the successor node for short. Since the left node is always smaller than the right node and parent node, the successor node has no left child node, and there may be right child nodes. By replacing the node with a successor node, it can ensure that the node is still a binary search tree after deletion.
There are also two search methods
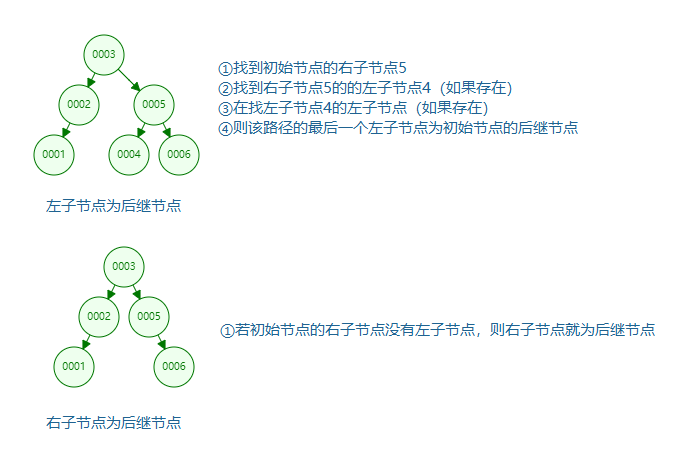
If the maximum value in the left subtree is used to replace
If the minimum value of the right subtree (successor node) is used to replace
code implementation
public class BSTTree {
/**
* node
*/
public static class Node {
//Data. In order to simplify the code, an int variable is stored in the default node of this program, and custom type variables can be stored in the actual program
int data;
//Left child node
Node leftChild;
//Right child node
Node rightChild;
public Node(int data) {
this.data = data;
}
@Override
public String toString() {
return "Node{" +
"data=" + data +
", leftChild=" + leftChild +
", rightChild=" + rightChild +
'}';
}
}
/**
* New nodes are added recursively
*
* @param root Root node
* @param data Inserted data
* @return
*/
public static Node insert(Node root, int data) {
if (root == null) {
root = new Node(data);
return root;
}
//If the inserted data is smaller than the root node, it is inserted into its left subtree
if (data <= root.data) {
root.leftChild = insert(root.leftChild, data);
} else {
//Insert into its right subtree
root.rightChild = insert(root.rightChild, data);
}
return root;
}
/**
* Preorder traversal
*
* @param root
*/
public static void preOrder(Node root) {
if (root != null) {
System.out.println(root.data + "->");
preOrder(root.leftChild);
preOrder(root.rightChild);
}
}
/**
* Medium order traversal
*
* @param root
*/
public static void inOrder(Node root) {
if (root != null) {
inOrder(root.leftChild);
System.out.print(root.data + "->");
inOrder(root.rightChild);
}
}
/**
* Postorder traversal
*
* @param root
*/
public static void postOrder(Node root) {
if (root != null) {
postOrder(root.leftChild);
postOrder(root.rightChild);
System.out.print(root.data + "->");
}
}
/**
* Find data
*
* @param data
* @return
*/
public static Node find(Node root, int data) {
//If the searched data is smaller than the root node, search to the left (or recursively)
Node current = root;
while (current != null) {
if (data < current.data) {
current = current.leftChild;
} else if (data > current.data) {
//Find right
current = current.rightChild;
} else {
return current;
}
}
return null;
}
/**
* minimum value
*
* @param root
* @return
*/
public static Node minimum(Node root) {
if (root == null) {
return null;
}
while (root.leftChild != null) {
root = root.leftChild;
}
return root;
}
/**
* Maximum
*
* @param root
* @return
*/
public static Node maximum(Node root) {
if (root == null) {
return null;
}
while (root.rightChild != null) {
root = root.rightChild;
}
return root;
}
/**
* Delete node
* 1.This node is a leaf node, that is, it has no child nodes
* 2.This node has a child node
* 3.The node has two child nodes (the node to be deleted is replaced by the subsequent nodes of the node,
* Because the successor node is smaller than the right node of the deleted node and larger than the left node of the deleted node)
* Intermediate successor node: the node with the second highest value than this node is the intermediate successor node, for example, the successor node of node 2 is 3
* 4
* / \
* 2 6
* / \ / \
* 1 3 5 8
*
* @param root
* @param data The value of the node to delete
*/
public static boolean delete(Node root, int data) {
//Used to represent the parent node of the node to be deleted
Node parent = null;
//Is the node to be deleted the left child of the parent node
boolean ifLeftChild = true;
//Nodes to be deleted
Node current = root;
//Locate the location of the deleted node and its parent node
while (true) {
if (data == current.data) {
break;
} else if (data < current.data) {
ifLeftChild = true;
parent = current;
current = current.leftChild;
} else if (data > current.data) {
ifLeftChild = false;
parent = current;
current = current.rightChild;
}
//If it cannot be found, return to fasle directly
if (current == null) {
return false;
}
}
//1. This node is a leaf node
if (current.leftChild == null && current.rightChild == null) {
//If it is the root node, delete the whole tree
if (current == root) {
root = null; //GC
}
//If left child node
if (ifLeftChild) {
parent.leftChild = null;
} else {
parent.rightChild = null;
}
}
//2. This node has a child node
if (current.leftChild != null && current.rightChild == null) {//If the left child node of the deleted node is not null
//If the node is the root node, the left child node of the root node becomes the root node
if (current == root) {
root = current.leftChild;
}
if (ifLeftChild) {
//Left: if the node is the left child node of the parent node, the left child node of the node becomes the left child node of the parent node
parent.leftChild = current.leftChild;
} else {
//Left, right and left: if the node is the left child node of the parent node, the left child node of the node becomes the right child node of the parent node
parent.rightChild = current.leftChild;
}
} else if (current.leftChild == null && current.rightChild != null) {
if (current == root) {
root = current.rightChild;
}
if (ifLeftChild) {
//Right, left and right: if the node is the left child node of the parent node, the right child node of the node becomes the left child node of the parent node
parent.leftChild = current.rightChild;
} else {
//Right: if the node is the right child node of the parent node, the right child node of the node becomes the right child node of the parent node
parent.rightChild = current.rightChild;
}
}
//3. This node has two child nodes, which can be deleted by subsequent nodes
if (current.leftChild != null && current.rightChild != null) {
//Gets the successor node that was deleted and rebuilt
Node successor = getSuccessor(current);
if (root == current) {
root = successor;
} else if (ifLeftChild) {
parent.leftChild = successor;
} else {
parent.rightChild = successor;
}
}
return true;
}
/**
* @param node The node to be deleted (assuming that the node has a right child node at this time)
* @return Delete the successor node of the node
*/
public static Node getSuccessor(Node node) {
//Left child node of node
Node leftChild = node.leftChild;
//Defines the parent node of the successor node
Node successorParent = node;
//Define successor nodes
Node successor = node;
//Define a temporary variable current. First get the right child node of the deleted node, and then get the minimum value of the right child node
Node current = node.rightChild;
//This step is to find the successor node of the deleted node
while (current != null) {
//Find the parent node of the following points
successorParent = successor;
successor = current;
//Get the minimum value of the right child node. The left child node of the straight left child tree is null, indicating that this node is the minimum value of the right child node of the deleted node
current = current.leftChild;
}
//After finding the successor node, rebuild the successor node tree
if (current != node.rightChild) {
/* The left child node of the parent node of the successor node changes from the original successor node to the right child node of the original successor node (because the value of the left child node is always less than the value of the parent node)
* If 55 is a successor node, 58 becomes the left child node of 60
* 60 55
* / \ \
* 55 80 ---Rebuild --- 60
* \ / \
* 58 58 80
*/
successorParent.leftChild = successor.rightChild;
successor.rightChild = node.rightChild;
successor.leftChild = leftChild;
}
return successor;
}
public static void main(String[] args) {
/*
* Add operation
* 4
* / \
* 2 6
* / \ / \
* 1 3 5 8
* /
* 7
*/
Node root = null;
root = insert(root, 4);
root = insert(root, 2);
root = insert(root, 1);
root = insert(root, 3);
root = insert(root, 6);
root = insert(root, 5);
root = insert(root, 8);
root = insert(root, 7);
// root = insert(root, 50);
// root = insert(root, 25);
// root = insert(root, 15);
// root = insert(root, 35);
// root = insert(root, 5);
// root = insert(root, 20);
// root = insert(root, 30);
// root = insert(root, 40);
//delete(root, 25);
inOrder(root);
// System.out.println("---------");
// //Find operation 4
// Node node = find(root, 4);
// printTree(node);
// System.out.println("---------");
// //Delete operation
// Node delete = delete(root, 4);
// printTree(delete);
}
/**
* Print
*
* @param root
*/
public static void printTree(Node root) {
System.out.println("Root node" + root.data);
if (root.leftChild != null) {
System.out.print("Left child node:");
printTree(root.leftChild);
}
if (root.rightChild != null) {
System.out.print("Right child node:");
printTree(root.rightChild);
}
}
}
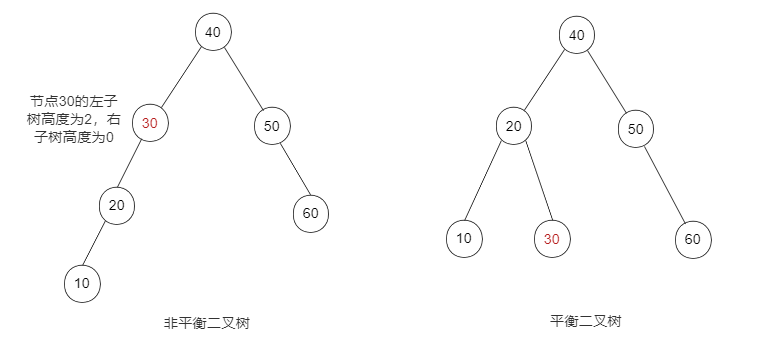
Balanced binary tree (AVL)
Balanced binary tree (AVL) is a binary sort tree. At the same time, the absolute value of the height difference (or balance factor, abbreviated as BF) between the left and right subtrees of any node does not exceed 1, and the left and right subtrees also meet.
Why use balanced binary tree
Through the search operation of binary search tree, it can be found that the search efficiency of a binary search tree depends on the height of the tree. If the height of the tree is the lowest, the search efficiency of the tree will also become higher.
For example, the following binary tree is all composed of right subtrees
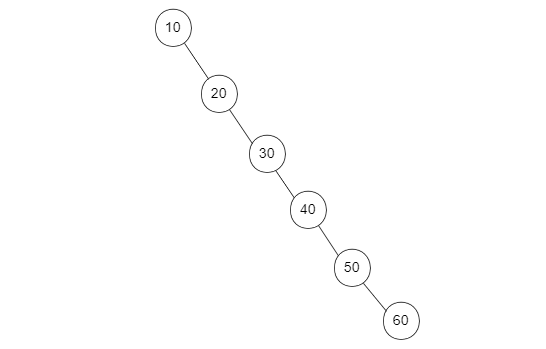
At this time, the binary tree is actually similar to a linked list. At this time, the lookup time complexity is O(n), while the lookup time complexity of AVL tree is O(logn). As mentioned earlier, O(logn) takes less time than O(n), as follows:
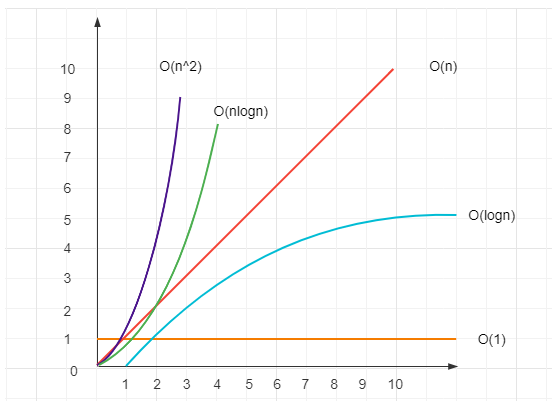
Refer to: Time complexity of common data structures
Adjustment of balanced binary tree
The insertion operation of a balanced binary tree will have two results:
If the balance is not broken, that is, BF=1 at any node, no adjustment is required
If the balance is broken, it needs to be adjusted by rotation, and the node is an imbalance node
An unbalanced binary tree can be rebalanced through the following adjustments:
Left rotation: take a node as a fulcrum (rotation node), its right child node becomes the parent node of the rotation node, the left child node of the right child node becomes the right child node of the rotation node, and the left child node remains unchanged
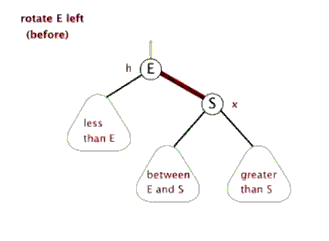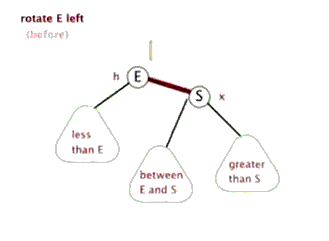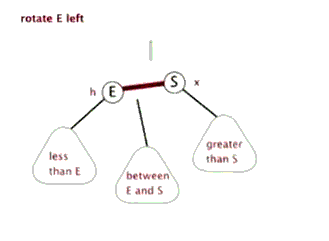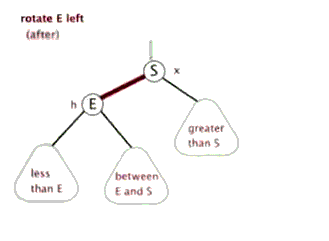
Right rotation: take a node as a fulcrum (rotation node), its left child node becomes the parent node of the rotation node, the right child node of the left child node becomes the left child node of the rotation node, and the right child node remains unchanged
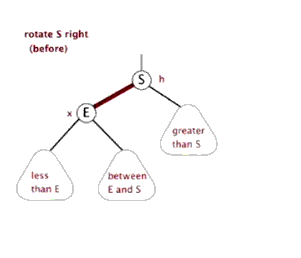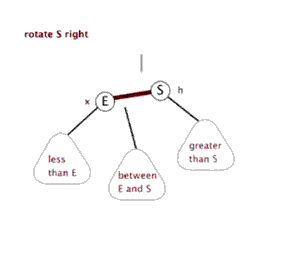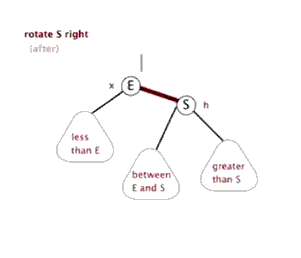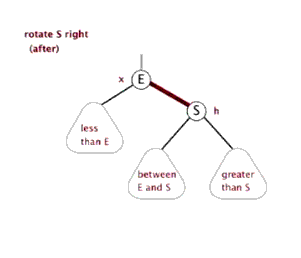
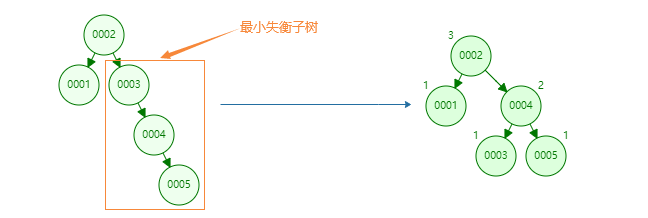
Imbalance adjustment is achieved by rotating the minimum imbalance subtree:
Add a new node in a balanced binary tree and look up the new node. The node whose absolute value of the first balance factor exceeds 1 (BF > 1) is the root subtree, which is called the minimum unbalanced subtree. In other words, an unbalanced tree may have multiple subtrees unbalanced at the same time. At this time, only the smallest unbalanced subtree needs to be adjusted.
After reading the following rotation methods, it will be clear to look back at the rotation of the minimum unbalanced subtree
LL rotation
Insert a new node into the left child (L) of the left subtree (L)
The inserted node is on the left of the left subtree of the unbalanced node, and the balance can be achieved after one right rotation, as shown below
-
Insert the new node 5, and the old root node 40 is an unbalanced node
-
The old root node 40 is the right subtree of the new root node 20
-
The right subtree 30 of the new root node 20 is the left subtree of the old root node 40
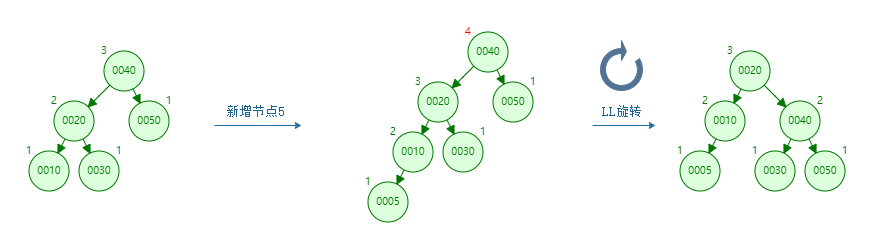
Rotation process
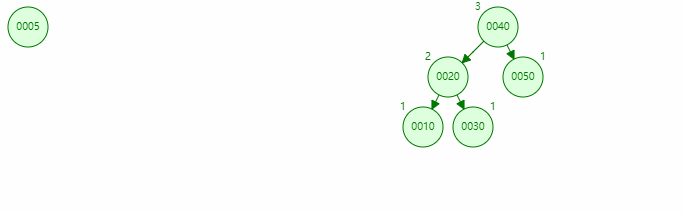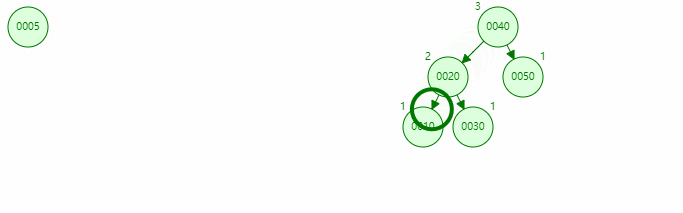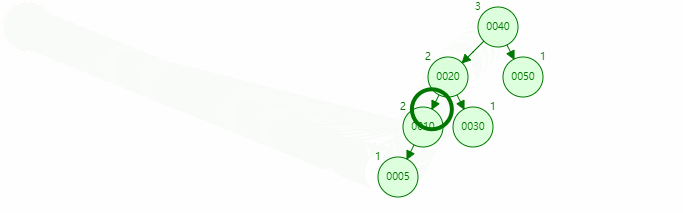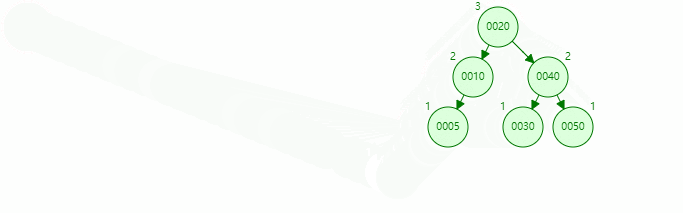
RR rotation
The inserted node is on the right side of the right subtree of the unbalanced node, and the balance can be achieved after one left rotation, as shown below
-
Insert the new node 60, and the old root node 20 is an unbalanced node
-
The old root node 20 is the left subtree of the new root node 40
-
The left subtree 30 of the new root node 40 is the right subtree of the old root node 20
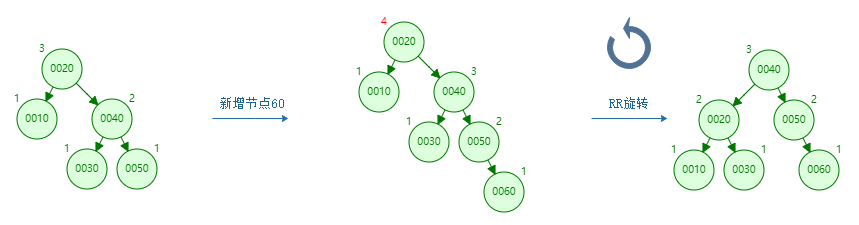
Rotation process

LR rotation
The inserted node is on the right side of the left subtree of the unbalanced node. Rotate left and then right, as shown below
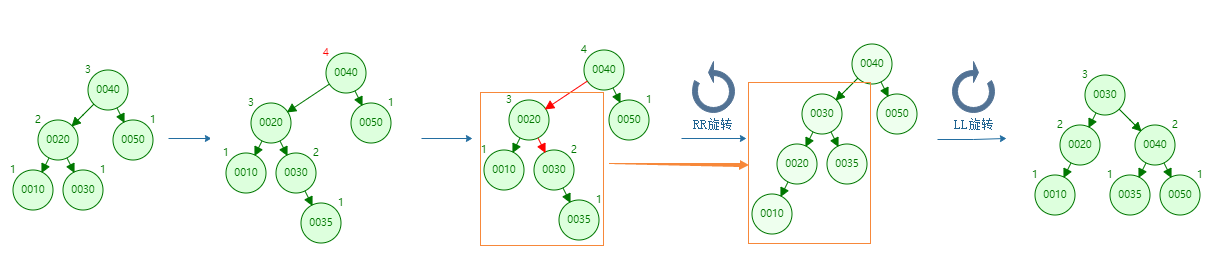
Rotation process
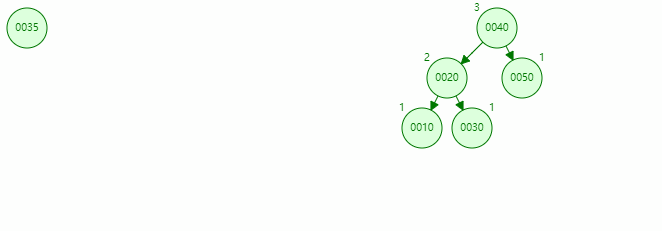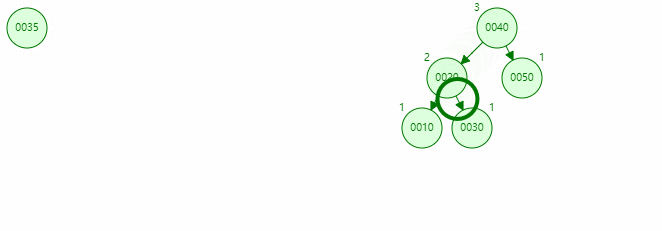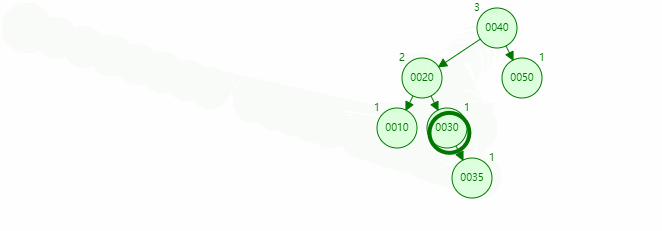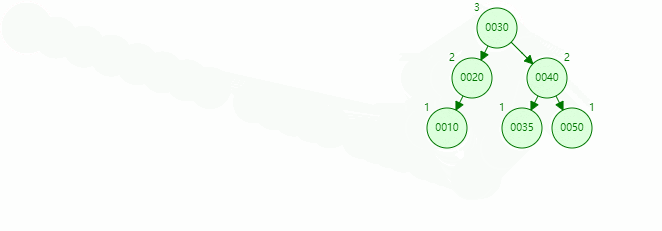
RL rotation
The insertion node is on the left side of the right subtree of the unbalanced node, rotating right first and then left, as shown below

Rotation process

code implementation
public class AVLTree {
//node
public static class Node {
int data; //data
Node leftChild; //Left child node
Node rightChild;//Right child node
int height; // Record the height of the node
public Node(int data) {
this.data = data;
}
}
//Gets the height of the node
public static int getHeight(Node p){
return p == null ? -1 : p.height; // The height of the empty tree is - 1
}
public static void main(String[] args) {
Node root = null;
root = insert(root,40);
root = insert(root,20);
root = insert(root,50);
root = insert(root,10);
root = insert(root,30);
//The inserted node is on the left of the left subtree of the unbalanced node
root = insert(root,5);
//To print a tree, print the left subtree first and then the right subtree
printTree(root);
}
public static void printTree(Node root) {
System.out.println(root.data);
if(root.leftChild !=null){
System.out.print("left:");
printTree(root.leftChild);
}
if(root.rightChild !=null){
System.out.print("right:");
printTree(root.rightChild);
}
}
// Insertion method of AVL tree
public static Node insert(Node root, int data) {
if (root == null) {
root = new Node(data);
return root;
}
if (data <= root.data) { // Insert into its left subtree
root.leftChild = insert(root.leftChild, data);
//Balance adjustment
if (getHeight(root.leftChild) - getHeight(root.rightChild) > 1) {
if (data <= root.leftChild.data) { // The inserted node is on the left of the left subtree of the unbalanced node
System.out.println("LL rotate");
root = LLRotate(root); // LL rotation adjustment
}else{ // The inserted node is on the right side of the left subtree of the unbalanced node
System.out.println("LR rotate");
root = LRRotate(root);
}
}
}else{ // Insert on its right subtree
root.rightChild = insert(root.rightChild, data);
//Balance adjustment
if(getHeight(root.rightChild) - getHeight(root.leftChild) > 1){
if(data <= root.rightChild.data){//The inserted node is on the left of the right subtree of the unbalanced node
System.out.println("RL rotate");
root = RLRotate(root);
}else{
System.out.println("RR rotate");//The inserted node is on the right side of the right subtree of the unbalanced node
root = RRRotate(root);
}
}
}
//Readjust the height value of the root node
root.height = Math.max(getHeight(root.leftChild), getHeight(root.rightChild)) + 1;
return root;
}
/**
* LR rotate
*/
public static Node LRRotate(Node p){
p.leftChild = RRRotate(p.leftChild); // First, RR rotate the left subtree of the unbalance point p
return LLRotate(p); // Then perform LL balance rotation on the unbalance point p and return a new node to replace the original unbalance point p
}
/**
* RL rotate
*/
public static Node RLRotate(Node p){
p.rightChild = LLRotate(p.rightChild); // Firstly, the right subtree of the imbalance point p is rotated in LL balance
return RRRotate(p); // Then perform RR balance rotation on the imbalance point p and return a new node to replace the original imbalance point p
}
/*
* LL rotate
* Schematic diagram of right rotation (right rotation of node 20)
* 40 20
* / \ / \
* 20 50 10 40
* / \ LL Rotation / /\
* 10 30 5 30 50
* /
* 5
*/
public static Node LLRotate(Node p){ // 40 is the unbalance point
Node lsubtree = p.leftChild; //The root node 20 of the left subtree of the unbalance point is used as the new node
p.leftChild = lsubtree.rightChild; //The right subtree 30 of the new node becomes the left subtree of the imbalance point 40
lsubtree.rightChild = p; // Take the unbalance point 40 as the right subtree of the new node
// Reset the height of the unbalance point 40 and the new node 20
p.height = Math.max(getHeight(p.leftChild), getHeight(p.rightChild)) + 1;
lsubtree.height = Math.max(getHeight(lsubtree.leftChild), p.height) + 1;
return lsubtree; // The new root node replaces the position of the original imbalance point
}
/*
* RR rotate
* Schematic diagram of left rotation (left rotation of node 20)
* 20 40
* / \ / \
* 10 40 20 50
* / \ RR Rotate / \
* 30 50 10 30 60
* \
* 60
*/
public static Node RRRotate(Node p){ // 20 is the unbalance point
Node rsubtree = p.rightChild; //The root node 40 of the right subtree of the imbalance point is used as the new node
p.rightChild = rsubtree.leftChild; //The left subtree 30 of the new node becomes the right subtree of the imbalance point 20
rsubtree.leftChild = p; // Take the unbalance point 20 as the left subtree of the new node
// Reset the height of the unbalance point 20 and the new node 40
p.height = Math.max(getHeight(p.leftChild), getHeight(p.rightChild)) + 1;
rsubtree.height = Math.max(getHeight(rsubtree.leftChild), getHeight(rsubtree.rightChild)) + 1;
return rsubtree; // The new root node replaces the position of the original imbalance point
}
}
summary
Those who can see this are cruel people. In fact, it's not difficult. I think it's very clear to understand the concepts of left-handed and right-handed. This article also took me a whole day. Basically, I contacted it from 0 to 1. If I'm interested, I can study it more.
Update record
| Modification time | Modification content |
|---|---|
| 2021-7-20 | Binary sort tree deletion (code logic error) |