Binary Search Tree Definition

A binary search tree is organized by a binary tree. Each node includes information such as left child, right child and parent besides Key. BST satisfies the restriction that for X of any node, the maximum value of keywords in his left subtree is <=X.key, and the minimum value of keywords in the right subtree is >=X.key.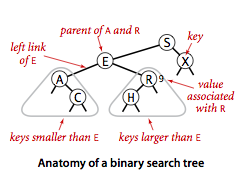

According to the above definition, an example of a binary search tree is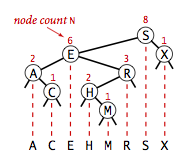

Binary Tree Operation

• query
• insert
• delete

Query (search)

According to the definition of binary search tree, the left subtree stores small values and the right subtree stores large values. A complete binary search schematic is as follows.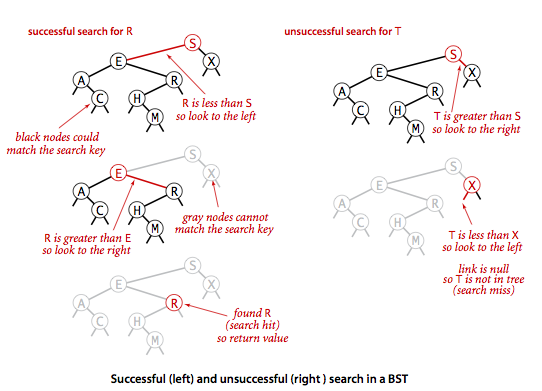

Can be written as pseudocode

TREE-SEARCH(x, k)
  if x == NULL  or k == x.key
    return x  
  if k < x.key
    return TREE-SEARCH(x.left)
  if k > x.key
    return TREE-SEARCH(x.right)

Convert to python code

def _get(self, key, node):
        if node is None:
            return None

        if key < node.key:
            return self._get(key, node.left)
        elif key > node.key:
            return self._get(key, node.right)
        else:
            return node.val
def get(self, key):
        """
        Return the value paired with 'key'

        Worst Case Complexity: O(N)

        Balanced Tree Complexity: O(lg N)
        """
        return self._get(key, self.root)

insert

Insertion and deletion are slightly more complex than queries, because this operation causes the size of the binary search tree to change the structure of the dynamic set. Insertion is slightly easier to implement than deletion. Insertion is divided into two parts.

• Query insertion node
• Change the data structure near the target node

The insertion process diagram is as follows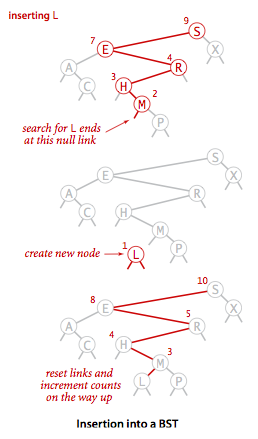

The corresponding pseudocode is as follows: input node z, Z. key = v, Z. left = NULL, Z. right = NULL.

TREE-INSERT(T, x)
  y = NULL
  x = T.root   # Start at the root node
  while x != NULL
    y = x      # Save the previous node
    if z.key < x.key # Left
      x = x.left
    else             # to the right
      x = x.right

  z.p = y        # Parent node
  if y == NULL   # tree T is empty
    T.root = z
  else if z.key < y.key
    y.left = z
  else y.right = z

The complexity of the program depends on the shape of the binary tree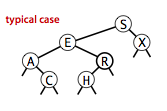

The running time of insertion depends on the height of the binary search tree h and the running time of the program O(h), so the shape of the binary tree directly affects the running time of the algorithm.

The python code is implemented as

def _put(self, key, val, node):

        # If we hit the end of a branch, create a new node
        if node is None:
            return Node(key, val)

        # Follow left branch
        if key < node.key:
            node.left = self._put(key, val, node.left)
        # Follow right branch
        elif key > node.key:
            node.right = self._put(key, val, node.right)
        # Overwrite value
        else:
            node.val = val

        node.size_of_subtree = self._size(node.left) + self._size(node.right)+1
        return node
def put(self, key, val):
          """
        Add a new key-value pair.

        Worst Case Complexity: O(N)

        Balanced Tree Complexity: O(lg N)
        """
        self.root = self._put(key, val, self.root)

delete

There are three cases of deletion:

• If deleting node x has no children, it can be deleted directly.
• If deleting node x has one child, replace the node with the child.

• The key is to find the successor of node x. The successor of node z has the smallest critical value in the right subtree of node z. In this case, the operation is divided into the following steps:

  1. Enter the node x to be deleted and the binary search tree T.
  2. The search begins in the right subtree of node x: find the minimum node H to the right and then to the left;
  3. The right child of H is the father node of H and the left child of H is the left child of X.

The sketch is as follows. It should be clear at a glance: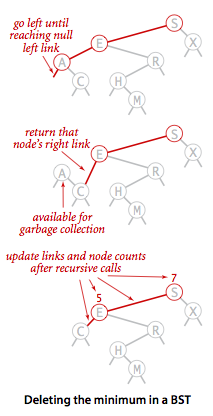

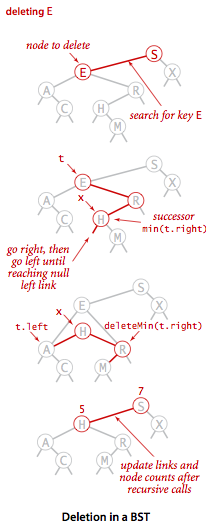
According to the above description, the deleted pseudocode can be divided into two parts:

1. In order to move the subtree, a subtree is replaced by a subtree and becomes a child node of both parents.

   TRANSPLANT(T, u, v)
   if u.p == NULL
   T.root = v
   else if u = u.p.left
   u.p.left = v
   else u.p.right = v
   
   if v!= NULL
   v.p = u.p

2. According to the first step, the deletion process of the binary search tree is completed.

   TREE-DELETE(T, z)
   if z.left = NULL
   TRANSPLANT(T, z, z.right)
   else if (z.right == NULL)
   TRANSPLANT(T, z, z.left)
   else
   y = TREE-MINIMUM(z.right)
   if y.p != z
   TRANSPLANT(T, y, y.right)
   y.right = z.right
   y.right.p = y
   TRANSPLANT(T, z, y)
   y.left = z.left
   y.left.p = y

   python is used to implement the following:

   def _delete(self, key, node):
   if node is None:
      return None
   if key < node.key:
      node.left = self._delete(key, node.left)
   elif key > node.key:
      node.right = self._delete(key, node.right)
   
   else:
      if node.right is None:
          return node.left
      elif node.left is None:
          return node.right
      else:
          old_node = node
          node = self._ceiling_node(key, node.right)
          node.right = self._delete_min(old_node.right)
          node.left = old_node.left
   node.size_of_subtree = self._size(node.left) + self._size(node.right)+1
   return node
   def _delete_min(self, node):
   if node.left is None:
      return node.right
   
   node.left = self._delete_min(node.left)
   node.size_of_subtree = self._size(node.left) + self._size(node.right)+1
   return node
   def _ceiling_node(self, key, node):
   """
   Returns the node with the smallest key that is greater than or equal to
   the given value 'key'
   """
   if node is None:
      return None
   
   if key < node.key:
      # Ceiling is either in left subtree or is this node
      attempt_in_left = self._ceiling_node(key, node.left)
      if attempt_in_left is None:
          return node
      else:
          return attempt_in_left
   elif key > node.key:
      # Ceiling must be in right subtree
      return self._ceiling_node(key, node.right)
   else:
      # Keys are equal so ceiling is node with this key
      return node

Reference

1. Introduction to Algorithms, 3rd Edition
2. http://algs4.cs.princeton.edu/32bst/