Binary search tree concept
Binary search tree is also called binary sort tree. It is either an empty tree or a binary tree with the following properties:
If its left subtree is not empty, the values of all nodes on the left subtree are less than those of the root node
If its right subtree is not empty, the values of all nodes on the right subtree are greater than those of the root node
Its left and right subtrees are also binary search trees
For example:

Implementation of binary search tree
Node class
First, implement a node class, which has three member variables:
template<class K>
struct BSTNode
{
BSTNode* _left;//Left pointer
BSTNode* _right;//Right pointer
K _key; //Node value
//Constructor
BSTNode(const K& key)
:_left(nullptr)
,_right(nullptr)
,_key(key)
{}
};
Main interface
template<class T>
class BSTree
{
typedef BSTNode<T> Node;
public:
BSTree()
:_root(nullptr)
{}
//insert
bool Insert(const K& key);
//lookup
Node* Find(const T& key);
//delete
bool Erase(const T& key);
//Deep copy
BSTree(const BSTree<K>& t);
//assignment
BSTree<K>& operator=(BSTree<K> t)
//Deconstruction
void Dostory(Node* root)
//Medium order traversal
void Inorder()
private:
Node* _root;//Points to the root node of the search tree
};
Iterative insertion
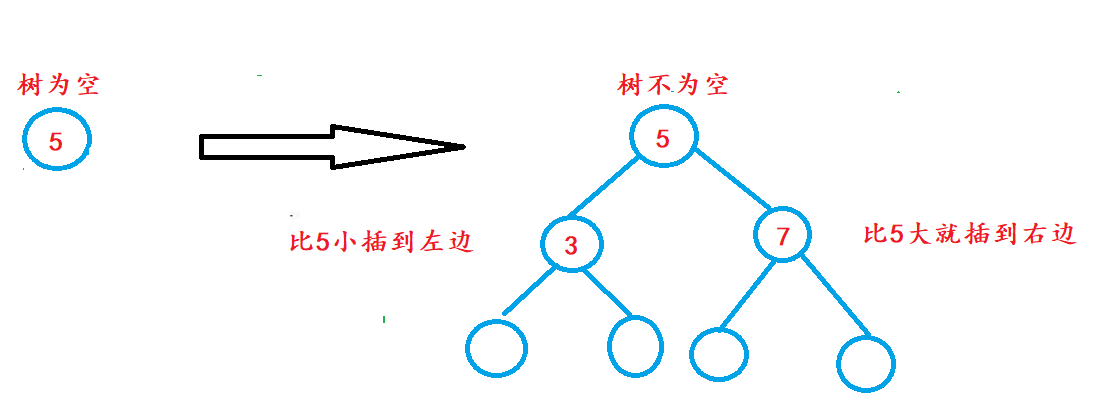
When the tree is empty, insert it directly. When the tree is not empty, for example, insert 7, which is larger than 5, the link is on the right of 5, insert 3, which is smaller than 5, and the link is on the left of 5.
Dynamic diagram demonstration:

Specific implementation:
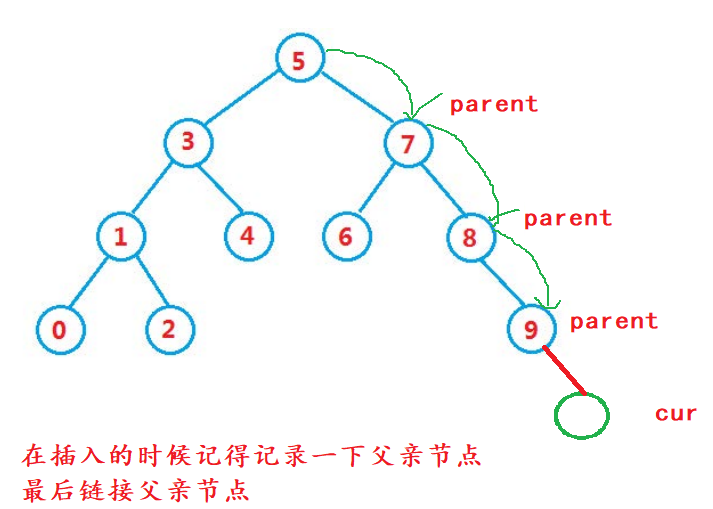
//Iterative insertion
bool Insert(const K& key)
{
//If the tree is empty, directly new a node
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
//The tree is not empty. The big one is inserted to the right and the small one to the left
Node* cur = _root;
Node* parent = cur;//Record the parent
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
//Found, start inserting
//Compared with his father, the big one is on his right and the small one is on his left
cur = new Node(key);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
The return value of the insertion interface of the search tree is bool, the success of insertion returns true, and the failure of insertion returns false. We can know whether the insertion is successful or not, and the value is the same as that allowed.
Recursive insertion
The idea of recursive implementation is basically the same. When the recursive inserted sub function accepts the parameter root, it should use a reference, so that it can be linked.
//Recursive insertion
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
//The subfunction is recommended to be private
bool _InsertR(Node*& root, const K& key)
{
//Empty tree direct insertion
if (root == nullptr)
{
root = new Node(key);
return true;
}
//If it is larger than key, it will recurse to the right
if (root->_key < key)
{
return _InsertR(root->_right,key);
}
//Recursive left when smaller than key
else if(root->_key > key)
{
return _InsertR(root->_left, key);
}
else
{
return false;
}
}
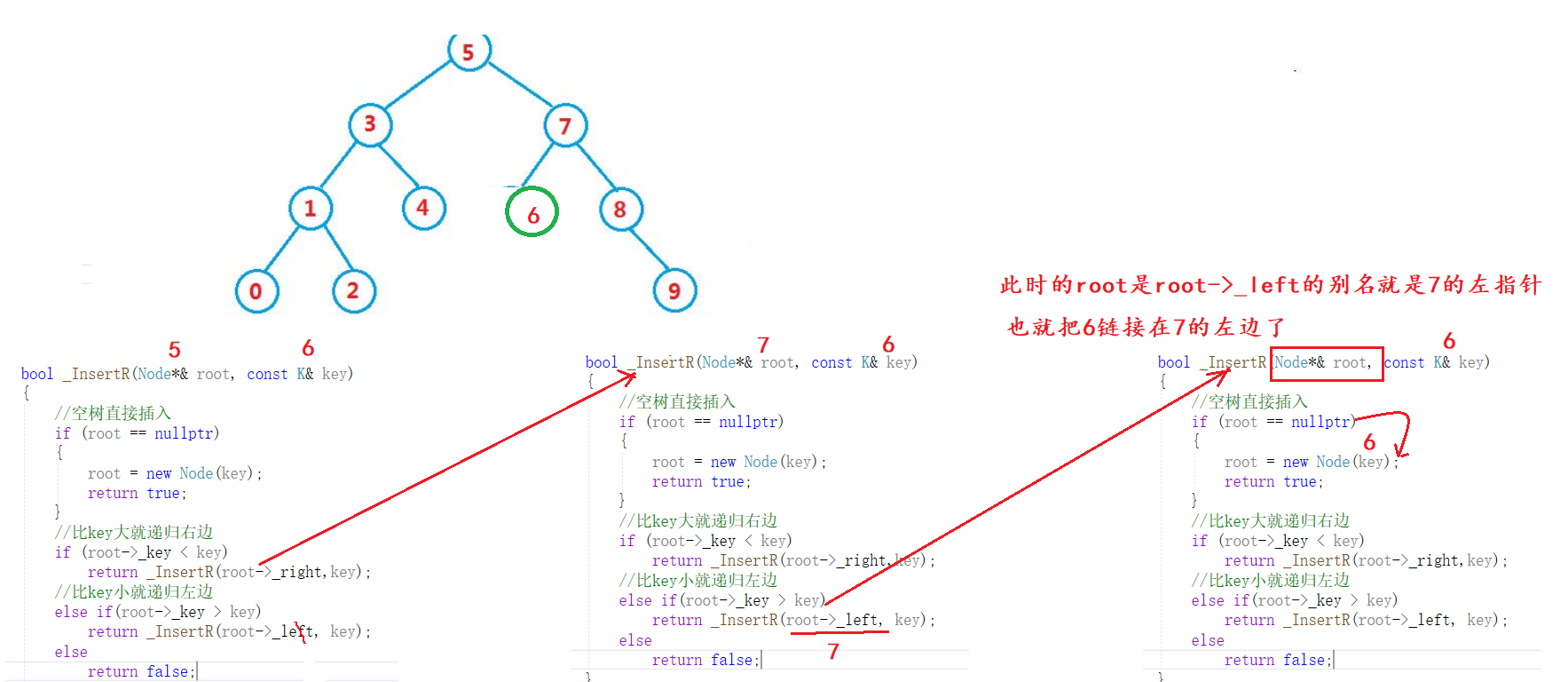
If you use a reference, you don't have to find the parent node. This reflects the value of reference.
Medium order traversal
The traversal of the search tree is recommended to use medium order traversal. Let's implement it and check whether the insertion we write is correct
//Medium order traversal
void Inorder()
{
_Inorder(_root);
cout << endl;
}
void _Inorder(Node* root)
{
//Return directly if the tree is empty
if (root == nullptr)
{
return;
}
//First recurse to the left, print the value, and then recurse to the right
_Inorder(root->_left);
cout << root->_key << " ";
_Inorder(root->_right);
}
Recursion diagram:

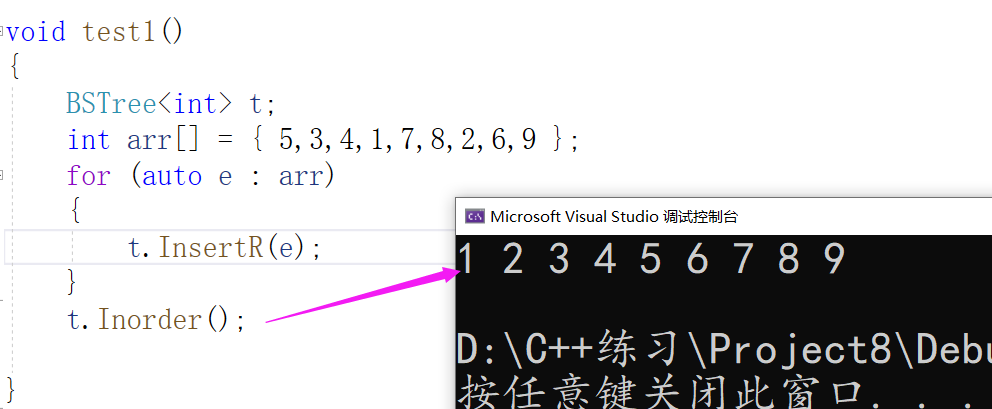
The recursive and non recursive inserts are now complete.
Iterative search
The search is much simpler. It is larger than the root node to the right and smaller to the left
Node* Find(const T& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return NULL;
}
recursive lookup
//recursive lookup
Node* FindR(const K& key)
{
return _FindR(_root, key);
}
Node* _FindR(Node*& root, const K& key)
{
if (root == nullptr)
{
return nullptr;
}
if (root->_key < key)
{
return _FindR(root->_right, key);
}
else if (root->_key > key)
{
return _FindR(root->_left, key);
}
else
{
return root;
}
}
Iterative deletion
The idea of deletion;
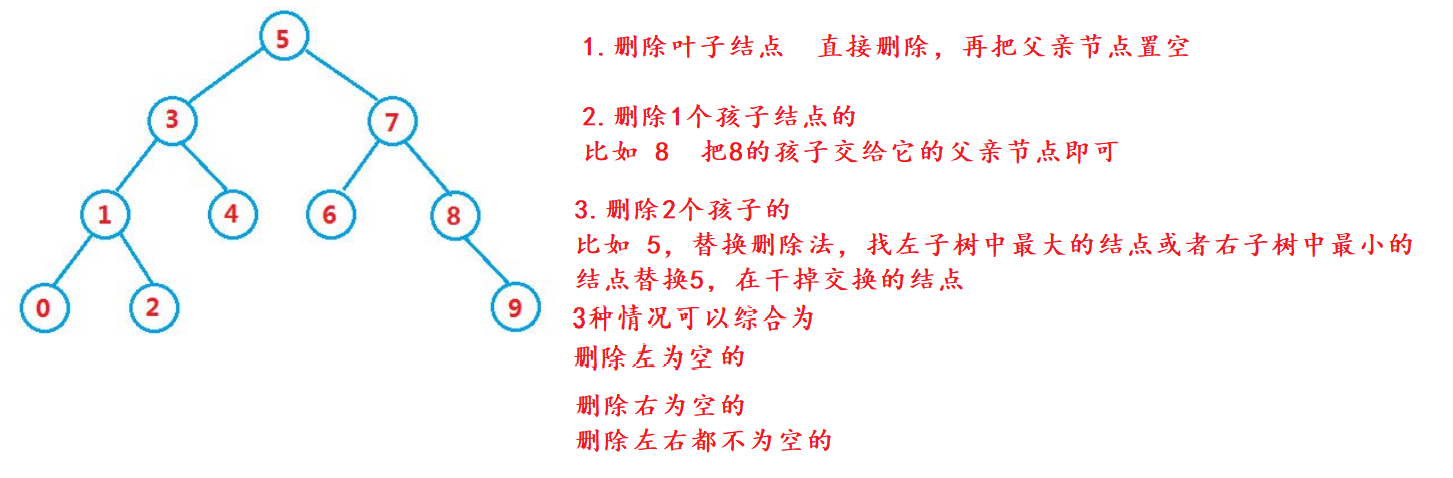
Delete analysis with empty left

Delete the detail root whose right is empty, and delete the left is the same. Draw and analyze
When discussing a wave of deletion, the left and right are not empty

Dynamic diagram demonstration;
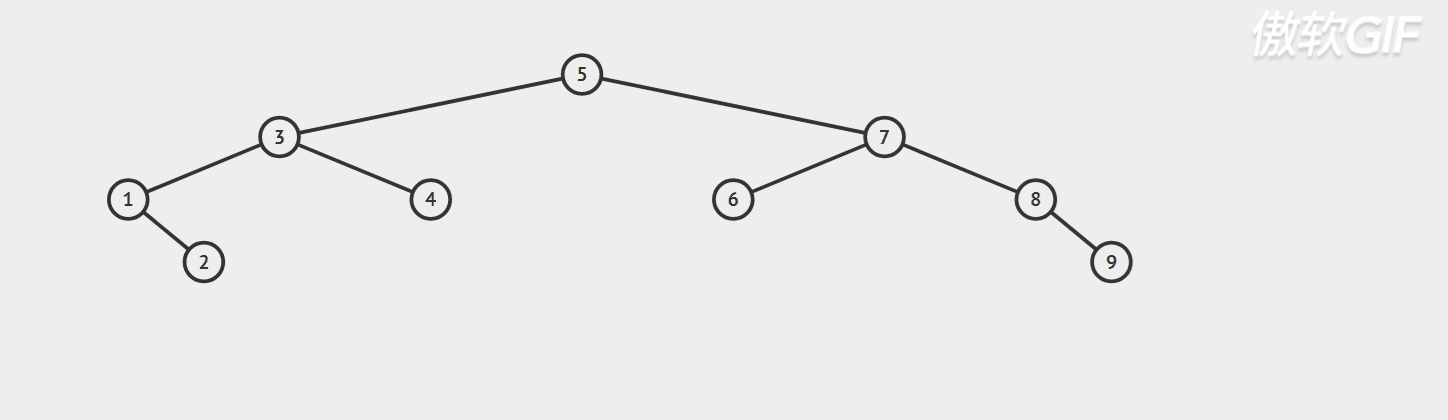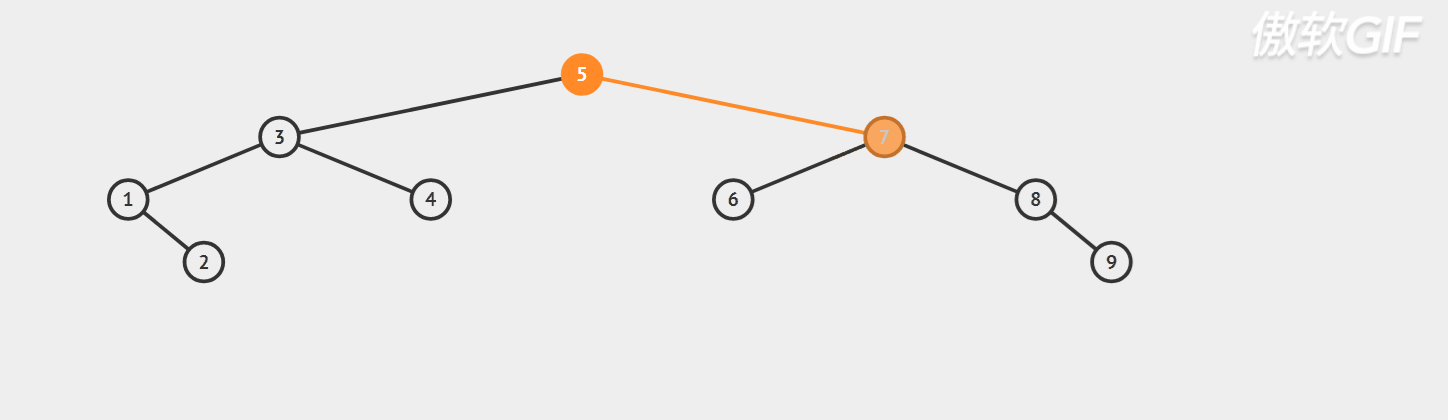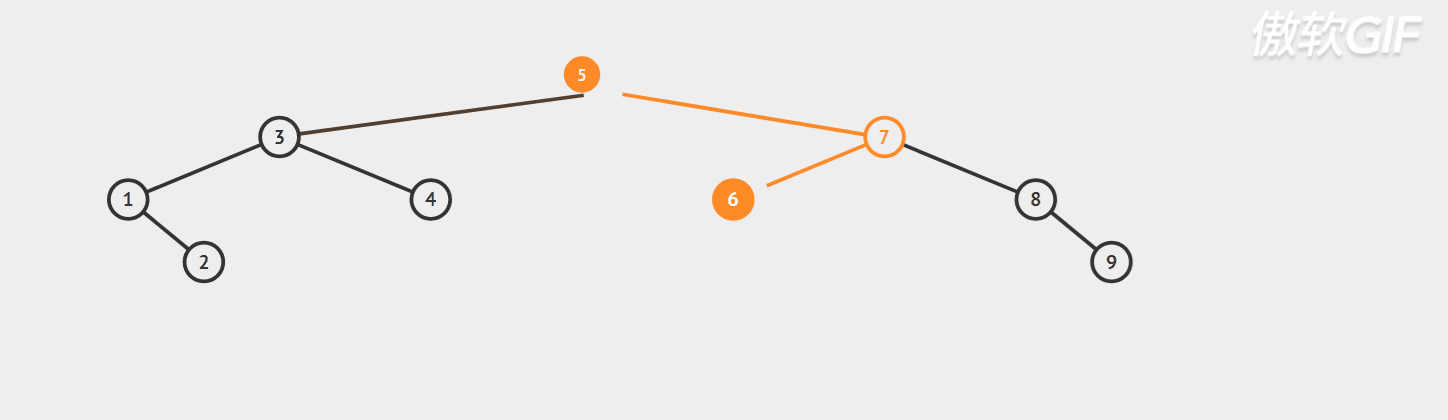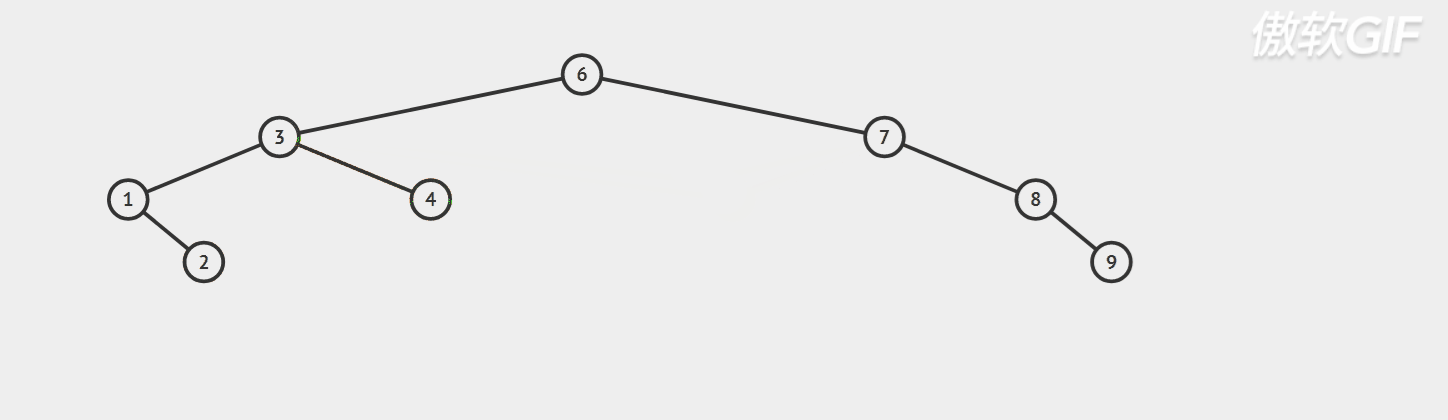
Specific code implementation:
bool Erase(const T& key)
{
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
//Start to find the node to delete
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
//Start deletion
//With one child
if (cur->_left == nullptr)
{
//There is no left subtree, let its right be the following node
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (parent->_right == cur)
{
parent->_right = cur->_right;
}
else
{
parent->_left = cur->_right;
}
}
delete cur;
return true;
}
else if (cur->_right == nullptr)
{
if(cur==_root)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
return true;
}
else
{
//If you have 2 children, delete it by substitution and find the smallest one in the right subtree
Node* minRight = cur->_right;
Node* minParent = cur;
while (minRight->_left)
{
minParent = minRight;//Record minRight's father
minRight = minRight->_left;//Look to the left
}
//Save key value
cur->_key = minRight->_key;
//Judge whether the node to be deleted is made by the father or right
if (minParent->_left == minRight)
{
minParent->_left = minRight->_right;
}
else
{
minParent->_right = minRight->_right;
}
delete minRight;
}
return true;
}
}
return false;
}
Recursive deletion
Idea of recursive deletion:

Specific code implementation:
//Recursive deletion
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
{
return false;
}
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else
{
//Found start deletion
if (root->_left == nullptr)
{
//Save the node to be deleted first
Node* del = root;
root = root->_right;
delete del;
}
else if (root->_right == nullptr)
{
//Save the node to be deleted first
Node* del = root;
root = root->_left;
delete del;
}
else
{
Node* minRight = root->_right;
//First find the smallest node of the right subtree
while (minRight->_left)
{
minRight = minRight->_left;
}
//Save the value of minRight first
K min = minRight->_key;
//Call yourself again
_EraseR(root->_right,min);
//Transpose the value of root to the value of min
root->_key = min;
}
return true;
}
}
Test the deletion. When testing, delete the tree
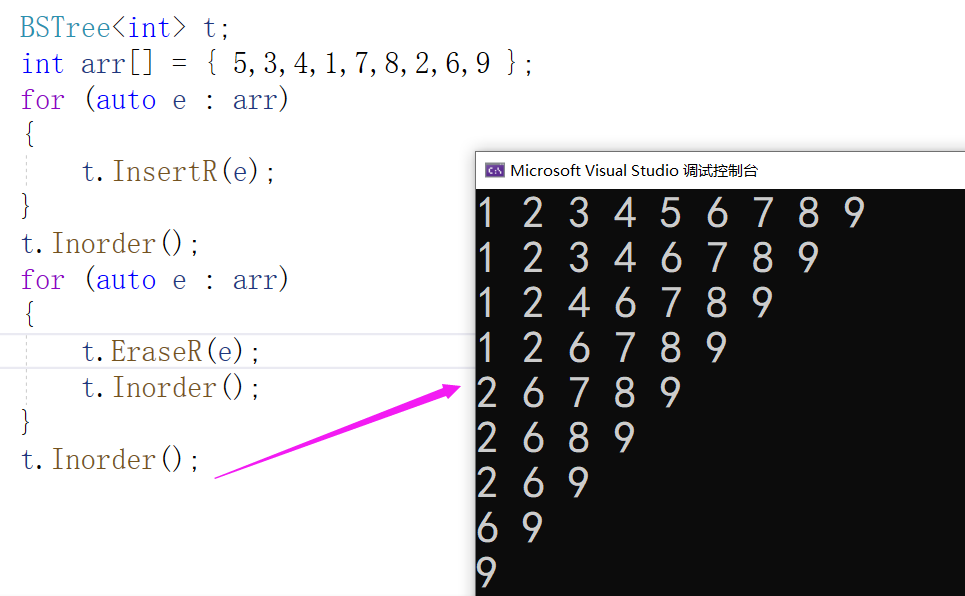
Deletion complete.
copy construction
First copy the value of the root node, then copy the left subtree and then the right subtree
//copy construction
BSTree(const BSTree<K>& t)
{
_root = _Copy(t._root);
}
Node* _Copy(Node* root)
{
if (root == nullptr)
{
return nullptr;
}
Node* copynode = new Node(root->_key);
//Copy left first, copy right
copynode->_left = _Copy(root->_left);
copynode->_right = _Copy(root->_right);
return copynode;
}
assignment
The assignment is the same as the previous vector and list. In modern writing, pass the value and exchange it
//Assign value, call copy construction, pass value, and then exchange
BSTree<K>& operator=(BSTree<K> t)
{
swap(_root, t._root);
return *this;
}

Deconstruction
Release the node according to the sequence of the binary tree, and finally set the pointer to the binary tree to null.
//Deconstruction
~BSTree()
{
_Destory(_root);
_root = nullptr;
}
void _Destory(Node* root)
{
if (root == nullptr)
{
return;
}
//Release left first, then right
_Destory(root->_left);
_Destory(root->_right);
delete root;
}
Application of search tree
K model
K model: in the K model, only the key is used as the key, and only the key needs to be stored in the structure. The key is the value to be searched
For example, give a word word and judge whether the word is spelled correctly. The specific methods are as follows:
Take each word in the word set as the key to build a binary search tree
Retrieve whether the word exists in the binary search tree. If it exists, it is spelled correctly, and if it does not exist, it is misspelled.
KV model
KV model: each key has a corresponding Value value, that is, the key Value pair of < key, Value >.
Each key has a corresponding Value value, that is, the key Value pair of < key, Value >. This way in real life
It is very common in life: for example, an English Chinese dictionary is the corresponding relationship between English and Chinese. The corresponding Chinese can be quickly found through English. English words and their corresponding Chinese < word, Chinese > form a key value pair
< word, Chinese meaning > constructs a binary search tree for key value pairs. Note: the binary search tree needs to be compared. When comparing key value pairs, only the key is compared. When querying English words, only the English words are given to quickly find the corresponding key.
Test code:
void test1()
{
kv::BSTree<string,string> dict;
dict.InsertR("basketball", "Basketball");
dict.InsertR("sun", "sun");
dict.InsertR("insert", "insert");
dict.InsertR("girl", "girl");
string str;
while (cin>>str)
{
kv::BSTNode<string, string>* ret = dict.FindR(str);
if (ret == nullptr)
{
cout << "The word is misspelled. The word is not in the thesaurus" << str << endl;
}
else
{
cout << "Chinese translation:" << ret->_value << endl;
}
}
}
The effects are as follows:

The Chinese meaning can be found only by entering words, which is the application of KV model.
KV model complete code
Complete code
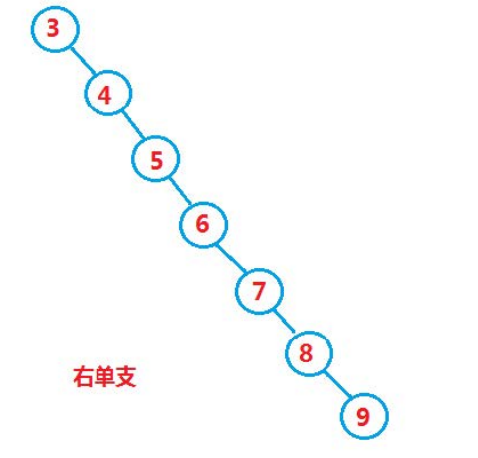
If the search tree becomes a single branch, the efficiency will not work. The right AVL tree and red black tree will be used to solve the problem.
