Binary sort tree (Java implementation)

1. Definition of binary sort tree

Binary sort tree, also called binary search tree, has the following properties if it is not empty:

• If its left subtree is not empty, the values of all nodes on the left subtree are smaller than the values of its root nodes;
• If its right subtree is not empty, the value of all nodes on the right subtree is greater than the value of its root node;

Its left and right subtrees are also binary sorting trees.

An important property of binary sort tree can be obtained from the definition: middle order traversing the binary tree can get an ordered sequence with increasing node value.

2. Node definition

//Nodes of binary sort tree
class Node{
    int value;//Stored element values
    Node left;//Left tree
    Node right;//Right subtree

    public Node(int value) {//Construction method
        this.value = value;
    }

    @Override
    public String toString() {//In order to see the result of traversal clearly, the toString() method is rewritten
        return "Node{" +
                "value=" + value +
                '}';
    }
}

3. Basic operation of binary sort tree

3.1 create a binary sort tree

Let's say we iterate through an array: {7,3,10,12,5,1,9, 2} According to the definition of binary sort tree, 7 is the root node of the tree, 3 < 7, 3 is the left subtree of 7, 10 > 7, 10 is the right subtree of 7; 12 > 7, traversing the right subtree of 7, 12 > 10, 12 is the right subtree of 10; 5 < 7, traversing the left subtree of 7, 5 > 3, 5 is the right subtree of 3; 1 < 7, traversing the left subtree of 7, 1 < 3, 1 is the left subtree of 3; 9 > 7, traversing the right subtree of 7, 9 < 10, 9 is the left subtree of 3 It is the left subtree of 10; 2 < 7, traversal in the left subtree of 7, 2 < 3, continue to traverse in the left subtree of 3, 2 > 1, so 2 is the right subtree of 1. After the above steps, the binary sorting tree is created. Obviously, the binary tree can be used recursively. Let's take a look at the structure of this tree to help you understand.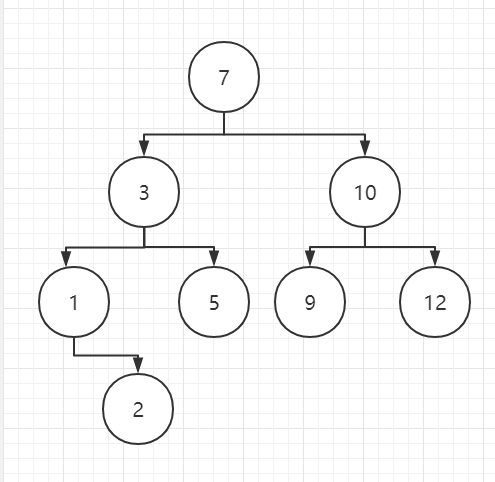

Many binary tree implementations on the Internet use C and C + +, which may not be very friendly to some students who only know Java (such as me), so after mastering the idea of creation, I implemented a wave of binary tree in Java. The code is as follows. The core method of creating binary tree is as follows:
(1) First, write the add() method in the node class (Node.java)

//How to add nodes
    public void add(Node node){
        if (node==null){//If the node to be added is empty, return directly
            return;
        }
        //Determine the relationship between the value of the incoming node and the value of the current node
        if (node.value<this.value){//The value of the node to be inserted < the value of the current node indicates that the node is to be inserted into the left subtree of the current node
            
            if (this.left==null){//If the left sub node of the current node is empty, the inserted node is directly regarded as the left sub tree of the current node
                this.left=node;
            }else {//If the left sub node of the current node is not empty, recursively add to the left sub tree
                this.left.add(node);
            }
        }else {//The value of the node to be inserted > = the value of the current node, indicating that the node is to be inserted into the right subtree of the current node
            if (this.right==null){//If the right sub node of the current node is empty, the inserted node is directly taken as the right sub tree of the current node
                this.right=node;
            }else {//If the left sub node of the current node is not empty, recursively add to the right sub tree
                this.right.add(node);
            }
        }
    }

(2) in the two fork sort tree class, the add() method in the node class is invoked so as to realize the addition. This processing is to reflect the characteristics of object-oriented programming and realize the decoupling between classes.

class BinarySortTree{//Create a binary sort tree
    private Node root;//Root node of tree
    //How to add nodes
    public void add(Node node){
        if (root==null){
            root=node;//If root is empty, direct root to node
        }else {
            root.add(node);
        }
    }
    //Sequential traversal
    public void infixOrder(){
        if (root!=null){
            root.infixOrder();
        }
        else {
            System.out.println("Binary sort tree is empty, unable to traverse");
        }
    }

(3) Test the creation of this BST (initial of binary sort tree):

public class BinarySortTreeDemo {
    public static void main(String[] args) {
        int [] arr={7,3,10,12,5,1,9,2};
        BinarySortTree binarySortTree = new BinarySortTree();
        for (int i = 0; i < arr.length; i++) {
            binarySortTree.add(new Node(arr[i]));
        }
        //Middle order traversal binary sort tree
        binarySortTree.infixOrder();
    }
}

The operation results are as follows: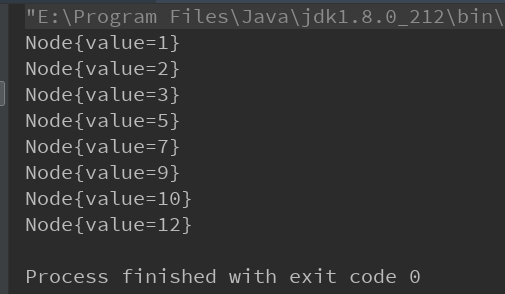

We find that the result of the middle order traversal is consistent with the size order of the elements, which shows that our binary tree creation is correct.

3.2 finding a node and a parent node of a binary sort tree

Set value to the value of the node to find

• If value = = value of the current node, the search succeeds and the node is returned.
• If value < the value of the current node, further recursively look up the left subtree.
• If value > the value of the current node, further recursively find the right subtree.

Code implementation:
(1) Write search() and searcheParent() methods in Node class

 public Node search(int value){
        if (this.value==value){//This node is found
            return this;
        }else if (value<this.value){//If the value to be found is less than the current node, recursively find the left subtree
            //If the left child node is empty, it will never be found again, and null is returned
            if (this.left==null){
                return null;
            }
            //If the left sub node is not empty, continue to search recursively, that is, the left sub node calls the search() method
            return this.left.search(value);
        }else {
            //If the right child node is empty, it will never be found again, and null is returned
            if (this.right==null){
                return null;
            }
            //If the right child node is not empty, continue to search recursively, that is, the left and right nodes call the search() method
            return this.right.search(value);
        }
    }
 /**
     * Find the parent node of a node
     * @param value The value of the node to find
     * @return Return if found, otherwise return null
     */
    public Node searchParent(int value){
        //If the current node is the parent of the node to be found, return
        if ((this.left!=null&&this.left.value==value)||
                (this.right!=null&&this.right.value==value)){
            return this;
        }else {
            //If the value to be found is less than the value of the current node, and the left node of the current node is not empty
            if (value<this.value&&this.left!=null){
                return this.left.searchParent(value);//Left subtree recursive search
            }else if (value>=this.value&&this.right!=null){
                return this.right.searchParent(value);//Recursive search of right subtree
            }else {
                return null;
            }
        }
    }

These two search methods need to be used later when deleting nodes.
(2) calling search() and searchParent() methods in BinarySortTree class.

 //Find the specified node
    public Node search(int value){
        if (root==null){
            return null;
        }else {
            return root.search(value);
        }
    }
    //Find the parent node to node
    public Node searchParent(int value){
        if (root==null){
            return null;
        }else {
            return root.searchParent(value);
        }
    }

3.3 deleting nodes

There are three situations to delete a node:

1. The deleted node is a leaf node
2. The deleted node has only left subtree or right subtree
3. The deleted node has both left and right subtrees

(1) Let's first look at the first case (delete 2|5|9|12):
(1.1) call the search(int value) method to find the node to be deleted and set it to targetNode;
(1.2) call the searchParent(int value) method to find the parent node of the node to be deleted, and set it to parentNode;
(1.3) determine whether it is parentNode.left=null or parentNode.right=null according to whether targetNode is the left or right child of parentNode.

(2) Let's look at the second case (delete 1):
(2.1) call the search(int value) method to find the node to be deleted and set it to targetNode;
(2.2) call searchParent(int value) method to find the parent node of the node to be deleted, and set it as parentNode;
(2.3) there are four basic situations: parentNode.left=targetNode.left or parentNode.right=targetNode.left or parentNode.left=targetNode.right or parentNode.right=targetNode.right. Of course, if the node to be deleted does not have a parent node, the node is the root node, then the node reference directly points to its left or right subtree, that is: root=targetNode.left or root=targetNode.right.
(3) Finally, let's look at the third case (delete 3):
(3.1) call the search(int value) method to find the node to be deleted and set it to targetNode;
(3.2) call the searchParent(int value) method to find the parent node of the node to be deleted, and set it to parentNode;
(3.3) find the smallest node of the left subtree in the right subtree of the node to be deleted, save the value of the minimum node, assign the value to the value of the node to be deleted, and then delete the minimum node, which realizes the operation of logically deleting the node with left subtree and right subtree.
For example, if you want to delete 3 here, you need to find the right subtree of 3, start to traverse from node 5, and then find the left subtree of 5. If it is 4, then assign the value of 4 to 3, and then delete the 4 node.
Obviously, this idea is also well understood. If you don't understand it, you can add my wechat communication: 973593026

Code implementation:

 /**
     * Returns the smallest node of the binary sort tree with node as the root node, and deletes the smallest node
     * @param node
     * @return
     */
    public int deleteRightTreeMin(Node node){
        Node target=node;
        //Loop through the left node to find the minimum
        while (target.left!=null){
            target=target.left;
        }
        //This is target, which points to the smallest node
        deleteNode(target.value);//Deleted
        return target.value;
    }
    //Delete the specified node
    public void deleteNode(int value){
        if (root==null){
            return;
        }else {
            Node targetNode = search(value);
            if (targetNode==null){//No nodes found to delete
                return;
            }
            //If targetNode does not have a parent
            if (root.left==null&&root.right==null){
                root=null;
            }
            //Parent of targetNode encountered
            Node parentNode = searchParent(value);
            //If the node to be deleted is a leaf node
            if (targetNode.left==null&&targetNode.right==null){
                //Determine whether the targetNode is the left or right child of the parent node
                if ((parentNode.left!=null)&&(parentNode.left.value==value)){
                    parentNode.left=null;
                }else if ((parentNode.right!=null)&&(parentNode.right.value==value)){
                    parentNode.right=null;
                }
            }else if (targetNode.left!=null&&targetNode.right!=null){//Delete a node with two subtrees
                int minVal = deleteRightTreeMin(targetNode.right);
                targetNode.value=minVal;
            }else {//Delete a node with only one subtree
                if (targetNode.left!=null){//Left child tree
                    if (parentNode!=null){
                        //If targetNode is the left child of parentNode
                        if (parentNode.left.value==value){
                            parentNode.left=targetNode.left;
                        }else {//targetNode is the right child of parentNode
                            parentNode.right=targetNode.left;
                        }
                    }else {
                        root=targetNode.left;
                    }

                }else {//Right subtree
                    if (parentNode!=null){
                        if (parentNode.left.value==value){
                            parentNode.left=targetNode.right;
                        }else {
                            parentNode.right=targetNode.right;
                        }
                    }else {
                        root=targetNode.right;
                    }

                }
            }
        }
    }

4. summary

In fact, binary sort tree is quite simple. The key is to master its thinking, so that the code problem can be solved. Here is the whole code. You can refer to it if you are interested. In addition, I have a deep understanding of the electronic resources of Java virtual machine (version 3), and I will add my wechat 973593026 to collect them if necessary.

package Day37;

/**
 * @Author Zhongger
 * @Description Binary sort tree: an array is created into a binary tree, and the binary tree is traversed by middle order traversal
 * @Date 2020.3.7
 */
public class BinarySortTreeDemo {
    public static void main(String[] args) {
        int [] arr={7,3,10,12,5,1,9,2};
        BinarySortTree binarySortTree = new BinarySortTree();
        for (int i = 0; i < arr.length; i++) {
            binarySortTree.add(new Node(arr[i]));
        }
        //Middle order traversal binary sort tree
        binarySortTree.infixOrder();

    }
}
class BinarySortTree{//Create a binary sort tree
    private Node root;
    /**
     * Returns the smallest node of the binary sort tree with node as the root node, and deletes the smallest node
     * @param node
     * @return
     */
    public int deleteRightTreeMin(Node node){
        Node target=node;
        //Loop through the left node to find the minimum
        while (target.left!=null){
            target=target.left;
        }
        //This is target, which points to the smallest node
        deleteNode(target.value);//Deleted
        return target.value;
    }

    //Find nodes to delete
    public Node search(int value){
        if (root==null){
            return null;
        }else {
            return root.search(value);
        }
    }
    //Find the parent of the node to delete
    public Node searchParent(int value){
        if (root==null){
            return null;
        }else {
            return root.searchParent(value);
        }
    }

    public void deleteNode(int value){
        if (root==null){
            return;
        }else {
            Node targetNode = search(value);
            if (targetNode==null){//No nodes found to delete
                return;
            }
            //If targetNode does not have a parent
            if (root.left==null&&root.right==null){
                root=null;
            }
            //Parent of targetNode encountered
            Node parentNode = searchParent(value);
            //If the node to be deleted is a leaf node
            if (targetNode.left==null&&targetNode.right==null){
                //Determine whether the targetNode is the left or right child of the parent node
                if ((parentNode.left!=null)&&(parentNode.left.value==value)){
                    parentNode.left=null;
                }else if ((parentNode.right!=null)&&(parentNode.right.value==value)){
                    parentNode.right=null;
                }
            }else if (targetNode.left!=null&&targetNode.right!=null){//Delete a node with two subtrees
                int minVal = deleteRightTreeMin(targetNode.right);
                targetNode.value=minVal;
            }else {//Delete a node with only one subtree
                if (targetNode.left!=null){//Left child tree
                    if (parentNode!=null){
                        //If targetNode is the left child of parentNode
                        if (parentNode.left.value==value){
                            parentNode.left=targetNode.left;
                        }else {//targetNode is the right child of parentNode
                            parentNode.right=targetNode.left;
                        }
                    }else {
                        root=targetNode.left;
                    }

                }else {//Right subtree
                    if (parentNode!=null){
                        if (parentNode.left.value==value){
                            parentNode.left=targetNode.right;
                        }else {
                            parentNode.right=targetNode.right;
                        }
                    }else {
                        root=targetNode.right;
                    }

                }
            }
        }
    }

    //How to add nodes
    public void add(Node node){
        if (root==null){
            root=node;//If root is empty, direct root to node
        }else {
            root.add(node);
        }
    }

    //Sequential traversal
    public void infixOrder(){
        if (root!=null){
            root.infixOrder();
        }
        else {
            System.out.println("Binary sort tree is empty, unable to traverse");
        }
    }
}

class Node{//node
    int value;
    Node left;
    Node right;

    public Node(int value) {
        this.value = value;
    }

    @Override
    public String toString() {
        return "Node{" +
                "value=" + value +
                '}';
    }


    /**
     * Find nodes to delete
     * @param value The value of the node to delete
     * @return Return the node if found, otherwise return null
     */
    public Node search(int value){
        if (this.value==value){//This node is found
            return this;
        }else if (value<this.value){//If the value to be found is less than the current node, recursively find the left subtree
            //If the left child node is empty
            if (this.left==null){
                return null;
            }
            return this.left.search(value);
        }else {
            //If the right child node is empty
            if (this.right==null){
                return null;
            }
            return this.right.search(value);
        }
    }

    /**
     * Find the parent of the node to delete
     * @param value The value of the node to delete
     * @return Return the node if found, otherwise return null
     */
    public Node searchParent(int value){
        //If the current node is the parent of the node to be deleted, return
        if ((this.left!=null&&this.left.value==value)||
                (this.right!=null&&this.right.value==value)){
            return this;
        }else {
            //If the value to be found is less than the value of the current node, and the left node of the current node is not empty
            if (value<this.value&&this.left!=null){
                return this.left.searchParent(value);//Left subtree recursive search
            }else if (value>=this.value&&this.right!=null){
                return this.right.searchParent(value);//Recursive search of right subtree
            }else {
                return null;
            }
        }
    }

    //How to add nodes
    public void add(Node node){
        if (node==null){
            return;
        }
        //Determine the relationship between the value of the incoming node and the value of the node of the current subtree
        if (node.value<this.value){
            //If the left child of the current node is empty
            if (this.left==null){
                this.left=node;
            }else {
                //Recursively add to left subtree
                this.left.add(node);
            }
        }else {//The value of the added node is greater than the value of the current node
            if (this.right==null){
                this.right=node;
            }else {//Recursively add to right subtree
                this.right.add(node);
            }
        }
    }

    //Sequential traversal
    public void infixOrder(){
        if (this.left!=null){
            this.left.infixOrder();
        }
        System.out.println(this);
        if (this.right!=null){
            this.right.infixOrder();
        }
    }
}