- Today we are going to solve two problems of constructing binary trees;
106. Construct binary tree from middle order and post order traversal sequences
105. Construct binary tree from preorder and inorder traversal sequences
First remember a conclusion: a binary tree can be uniquely constructed according to the pre order and middle order, and a binary tree can be uniquely constructed according to the middle order and post order, but the pre order and post order can't. Analysis below
1.leetcode106. Constructing binary tree from middle order and post order traversal sequences
According to the middle order traversal and post order traversal of a tree, a binary tree is constructed.
You can assume that there are no complex elements in the tree. For example, give
inorder = [9,3,15,20,7] postorder postorder = [9,15,7,20,3] returns the following binary tree:
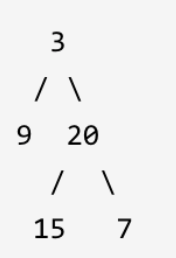
1.1 construction process
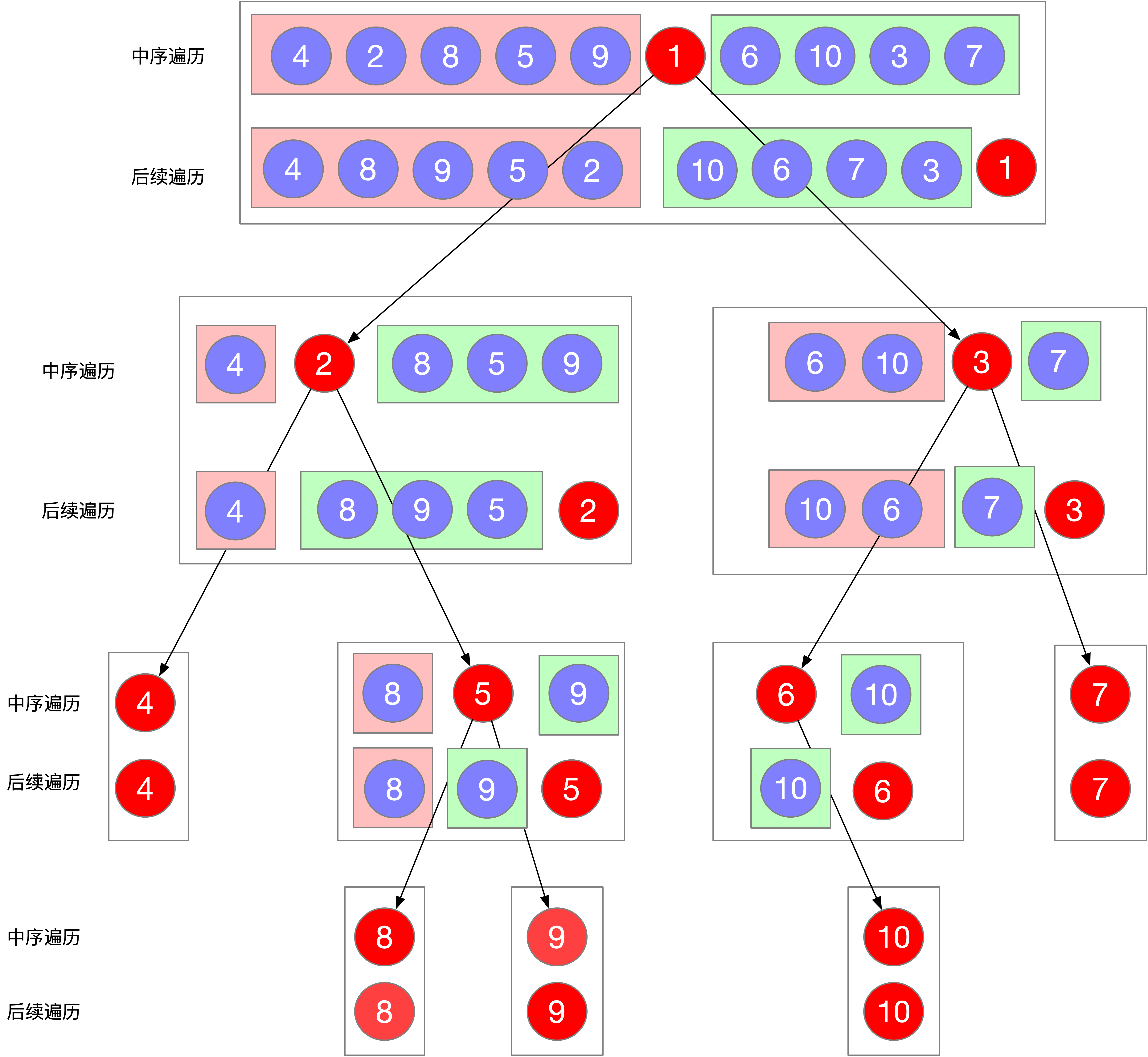
First, recall how to construct a unique binary tree according to two orders. I believe everyone should be clear about the theoretical knowledge, that is, the last element of the later ordered array is the cutting point, cut the middle ordered array first, and cut the back ordered array according to the middle ordered array. Cut down layer by layer. The last element of each subsequent array is the node element.
The key to solve this problem is to be familiar with what the traversal order of the tree represents, and it is best to draw the picture. The solution of this problem takes you to traverse the middle order and the subsequent binary tree, and then restore the binary tree according to the traversal results.
First, a tree
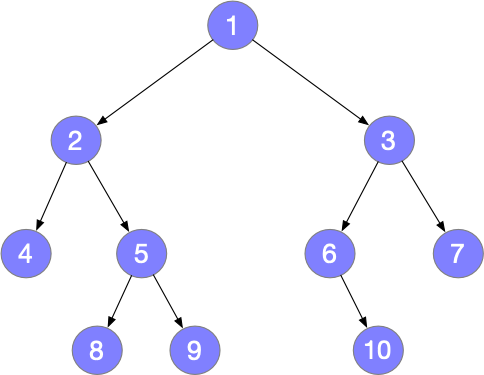
Then look at the traversal results of the tree:

Restore the binary tree according to the middle order and post order traversal results
Characteristics of medium order traversal and subsequent traversal
First, let's look at the two known conditions given by the topic, the order ergodic sequence and the post order ergodic sequence. According to the characteristics of these two ergodic sequences, we can draw two conclusions
- In the post order traversal sequence, the last element is the root node of the tree
- In the middle order traversal sequence, the left side of the root node is the left subtree, and the right side of the root node is the right subtree
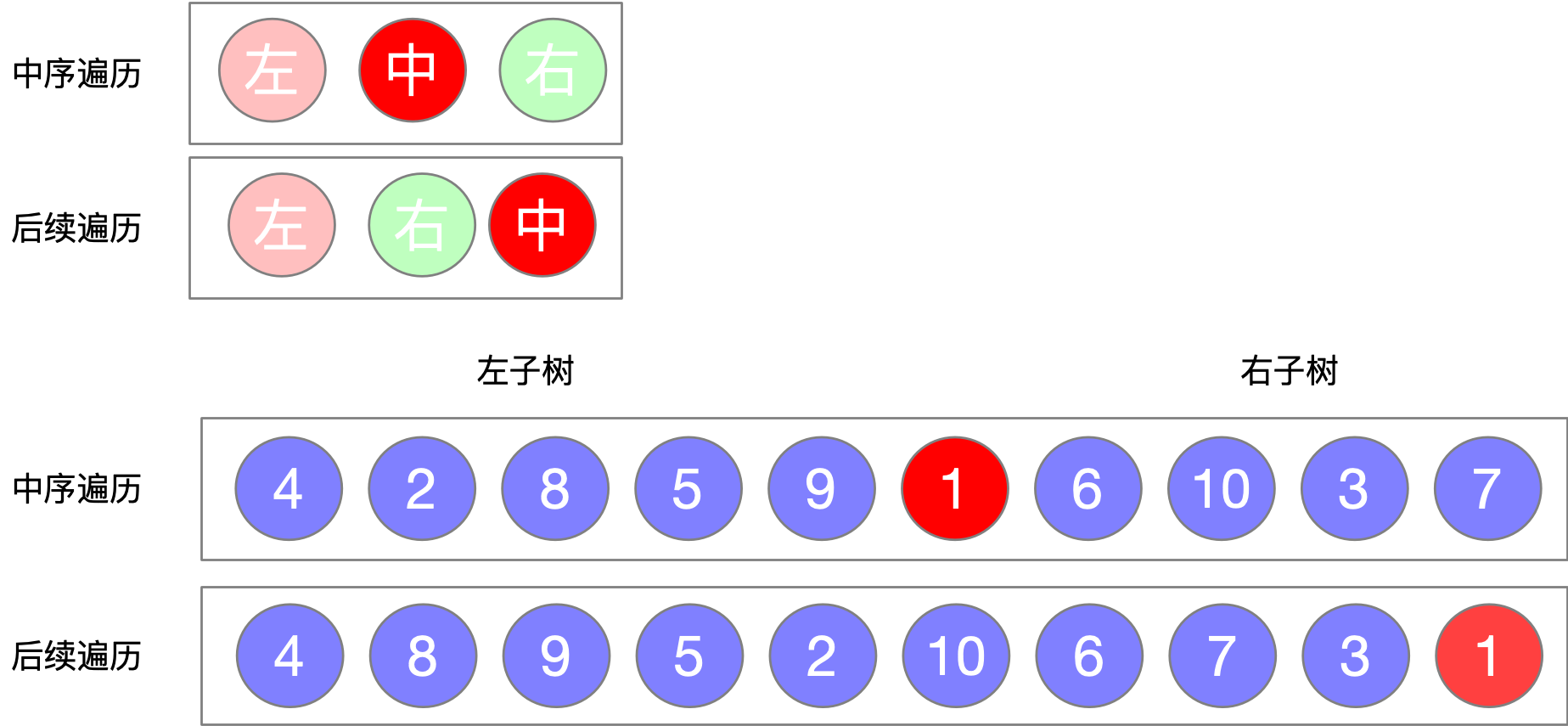
Tree restore process description
According to the characteristics of middle order traversal and subsequent traversal, we analyze the restoration process of the tree
- First, find the root node (the last element) in the subsequent traversal sequence
- Find the position of the root node in the middle order traversal sequence according to the root node
- According to the position of the root node, the middle order traversal sequence is divided into left subtree and right subtree
- According to the position of the root node, the left and right boundary positions of the left and right subtrees in the ordered array and subsequent arrays are determined
- Recursive construction of left subtree and right subtree
- End of return to root node
Tree restore process variable definition
Several variables need to be defined to help us restore the tree
- HashMap memo needs a hash table to store the positional relationship between elements and indexes in the middle order traversal sequence Because after getting the root node from the subsequent sequence, you need to find the corresponding position in the intermediate sequence, so as to divide the array into left subtree and right subtree
- int ri the index position of the root node in the middle order traversal array
- Two position markers [is, ie] of the array are traversed in middle order. Is is the start position and IE is the end position
- Two position marks [PS, pe] of the post order traversal array. PS is the start position and pe is the end position
Calculation of positional relationship
After finding the location of the root node, we need to determine the position of the left and right boundaries of the left and right subtrees in the medium order array and subsequent arrays in the next round.
- Left subtree - ordered array is = is, ie = ri - 1
- Left subtree - postorder array PS = PS, PE = PS + RI - is - 1 (the PE calculation process explains that the starting position of the subsequent array plus the length of the left subtree - 1 is the end position of the postorder array, and the length of the left subtree = root node index - left subtree)
- Right subtree - ordered array is = ri + 1, ie = ie
- Right subtree - postorder array ps = ps + ri - is, pe - 1
It doesn't matter if you don't understand. Just look at the picture. The calculation diagram is as follows:
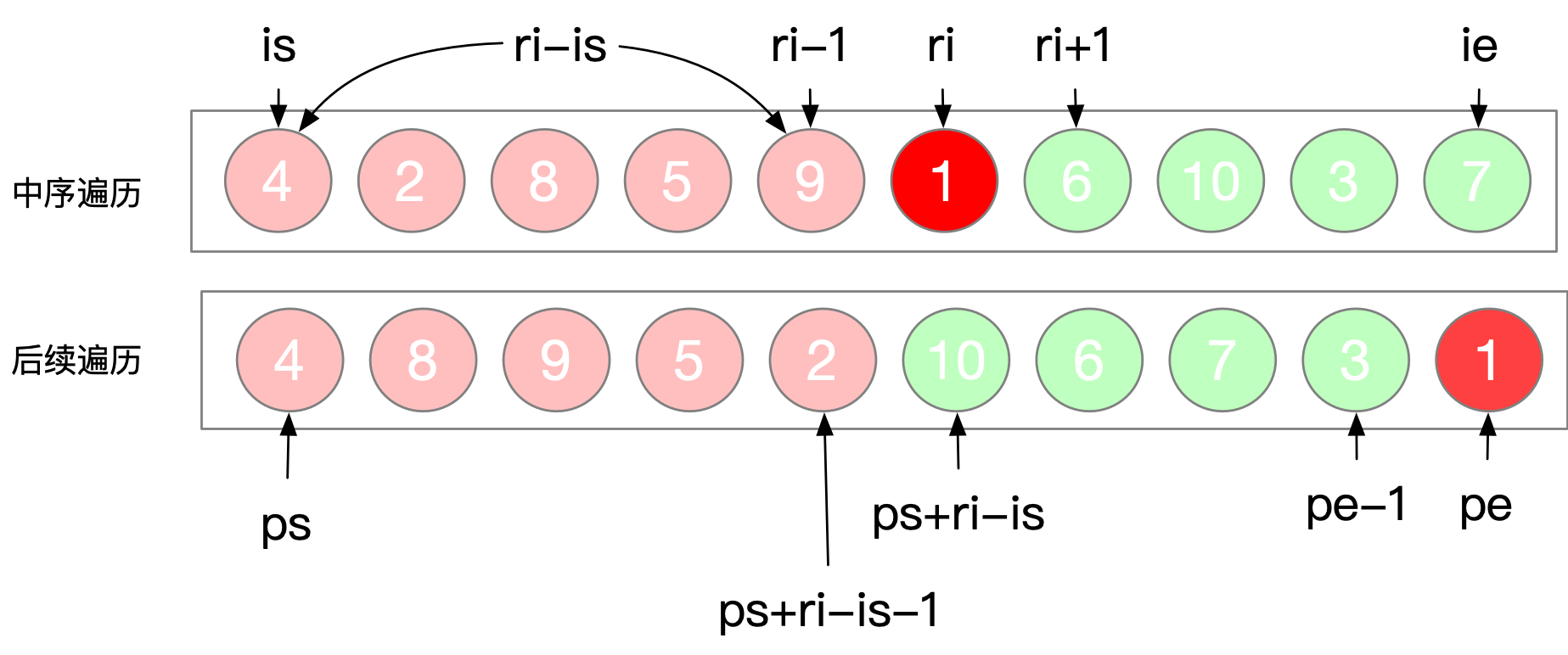
Tree restore process:
Finally, look at the code:
class Solution {
HashMap<Integer,Integer> memo = new HashMap<>();
int[] post;
public TreeNode buildTree(int[] inorder, int[] postorder) {
for(int i = 0;i < inorder.length; i++) memo.put(inorder[i], i);
post = postorder;
TreeNode root = buildTree(0, inorder.length - 1, 0, post.length - 1);
return root;
}
public TreeNode buildTree(int is, int ie, int ps, int pe) {
if(ie < is || pe < ps) return null;
int root = post[pe];
int ri = memo.get(root);
TreeNode node = new TreeNode(root);
node.left = buildTree(is, ri - 1, ps, ps + ri - is - 1);
node.right = buildTree(ri + 1, ie, ps + ri - is, pe - 1);
return node;
}
}
2.LeetCode105 constructs binary tree from preorder and inorder traversal sequences
I saw a very detailed analysis on the LeetCode website, which also burned my brain. I haven't fully understood it yet. I posted it directly to the original text first.
Solution 1: recursion
The order of first traversal is the root node, left subtree and right subtree. The middle order traversal order is the left subtree, the root node and the right subtree.
Therefore, we only need to get the root node according to the first order traversal, and then find the location of the root node in the middle order traversal. The left side is the node of the left subtree and the right side is the node of the right subtree.
The left subtree and right subtree can be generated recursively.
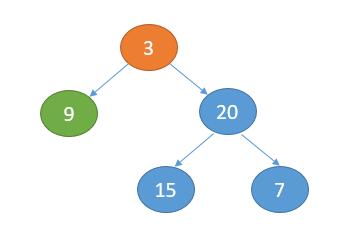
For example, let's analyze the example above.
preorder = [3,9,20,15,7]
inorder = [9,3,15,20,7]
First, according to preorder The root node found is 3
Then, according to the root node inorder It is divided into left subtree and right subtree
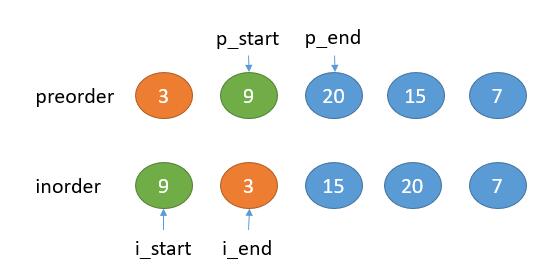
Left subtree
inorder [9]
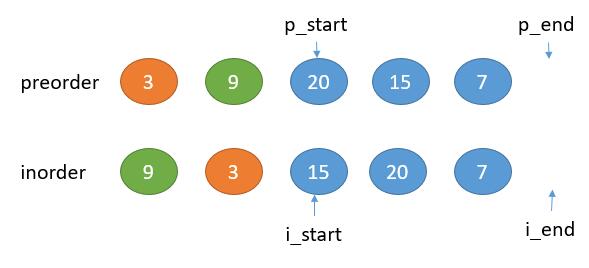
Right subtree
inorder [15,20,7]
The corresponding preorder traversal array is also added
Left subtree
preorder[9]
inorder [9]
Right subtree
preorder[20 15 7]
inorder [15,20,7]Now we only need to construct left subtree and right subtree, and successfully turn the big problem into a small problem
Then repeat the above steps to continue the division until both preorder and inorder are empty and return null
In fact, we don't really need to split preorder and inorder. We just need to point to the beginning and end positions with two pointers respectively. Note that the array range pointed to by the two pointers below includes the left boundary and does not include the right boundary.
For the synthesis of the tree below.
Left subtree
Right subtree:
public TreeNode buildTree(int[] preorder, int[] inorder) {
return buildTreeHelper(preorder, 0, preorder.length, inorder, 0, inorder.length);
}
private TreeNode buildTreeHelper(int[] preorder, int p_start, int p_end, int[] inorder, int i_start, int i_end) {
// preorder is null and returns null directly
if (p_start == p_end) {
return null;
}
int root_val = preorder[p_start];
TreeNode root = new TreeNode(root_val);
//Find the location of the root node in the middle order traversal
int i_root_index = 0;
for (int i = i_start; i < i_end; i++) {
if (root_val == inorder[i]) {
i_root_index = i;
break;
}
}
int leftNum = i_root_index - i_start;
//Recursive construction of left subtree
root.left = buildTreeHelper(preorder, p_start + 1, p_start + leftNum + 1, inorder, i_start, i_root_index);
//Recursive construction of right subtree
root.right = buildTreeHelper(preorder, p_start + leftNum + 1, p_end, inorder, i_root_index + 1, i_end);
return root;
}The above code is easy to understand, but there is a problem. To find the location of the root node in the middle order traversal, we have to traverse the middle order traversal array to find it every time. For reference, we can use a HashMap to save the value and subscript of each element of the middle order traversal array, so that we can find the location of the root node directly.
public TreeNode buildTree(int[] preorder, int[] inorder) {
HashMap<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < inorder.length; i++) {
map.put(inorder[i], i);
}
return buildTreeHelper(preorder, 0, preorder.length, inorder, 0, inorder.length, map);
}
private TreeNode buildTreeHelper(int[] preorder, int p_start, int p_end, int[] inorder, int i_start, int i_end,
HashMap<Integer, Integer> map) {
if (p_start == p_end) {
return null;
}
int root_val = preorder[p_start];
TreeNode root = new TreeNode(root_val);
int i_root_index = map.get(root_val);
int leftNum = i_root_index - i_start;
root.left = buildTreeHelper(preorder, p_start + 1, p_start + leftNum + 1, inorder, i_start, i_root_index, map);
root.right = buildTreeHelper(preorder, p_start + leftNum + 1, p_end, inorder, i_root_index + 1, i_end, map);
return root;
}
Thought it was perfect, in here Another bright idea is Stefan pochmann, who will be noticed when he often visits discussions and has more than 30000 praise.
He also found that he had to traverse once every time to find the trouble of traversing the root node in the array in the middle order, but he solved this problem without HashMap. Let's talk about it below.
Save the root node of the current tree to be constructed with the pre variable, recursively construct the left and right subtrees from the root node, the in variable points to the beginning of the available numbers of the current root node, and then there is a stop point for the current pre, from in to stop represents the current number range of the tree to be constructed.
public TreeNode buildTree(int[] preorder, int[] inorder) {
return buildTreeHelper(preorder, inorder, (long)Integer.MAX_VALUE + 1);
}
int pre = 0;
int in = 0;
private TreeNode buildTreeHelper(int[] preorder, int[] inorder, long stop) {
//null returned at the end
if(pre == preorder.length){
return null;
}
//null is returned when the stop point is reached
//The current stop point has been used. Move back in
if (inorder[in] == stop) {
in++;
return null;
}
int root_val = preorder[pre++];
TreeNode root = new TreeNode(root_val);
//The stop point of the left subtree is the current root node
root.left = buildTreeHelper(preorder, inorder, root_val);
//The stop point of the right subtree is the stop point of the current tree
root.right = buildTreeHelper(preorder, inorder, stop);
return root;
}
The code is simple, but it's really hard to understand if you think about it.
Post his original words.
Consider the example again. Instead of finding the 1 in inorder, splitting the arrays into parts and recursing on them, just recurse on the full remaining arrays and stop when you come across the 1 in inorder. That's what my above solution does. Each recursive call gets told where to stop, and it tells its subcalls where to stop. It gives its own root value as stopper to its left subcall and its parent`s stopper as stopper to its right subcall.
I wanted to make this algorithm clear, but it's still too difficult to make all kinds of drawings clear. Here we will draw some pictures of the process. We can only go through the code above and understand it.
3
/ \
9 7
/ \
20 15
Preorder traversal array and inorder traversal array
preorder = [ 3, 9, 20, 15, 7 ]
inorder = [ 20, 9, 15, 3, 7 ]
p representative pre,i representative in,s representative stop
First, construct a tree with root node 3. The available number is i reach s
s Initializing all numbers in a tree will not be equal, so one is used in the code long To represent
3, 9, 20, 15, 7
^
p
20, 9, 15, 3, 7
^ ^
i s
Consider the left subtree whose root node is 3, Consider the right subtree of the tree with root node 3,
stop The value is the value 3 of the current root node Only know stop Value is last s
The new root node is 9,The available numbers are i reach s
barring s
3, 9, 20, 15, 7 3, 9, 20, 15, 7
^
p
20, 9, 15, 3, 7 20, 9, 15, 3, 7
^ ^ ^
i s s
Recursive exit
3, 9, 20, 15, 7
^
p
20, 9, 15, 3, 7
^
i
s
here in and stop Equal indicates that no number is available, so it returns null,It also indicates that the root node of a tree has been reached at this time, so i Move back.
In short, his idea is that instead of looking for the location of the root node from the middle order traversal, he directly passes the value to indicate the end point of the current subtree. However, I still feel that I haven't got his point. The meaning of in and stop variables is also given by me. It only makes sense for the whole algorithm. You have good ideas to communicate with me.
Solution 2: iterative stack
Referring to here, we can use a stack and implement it iteratively.
Suppose the tree we want to restore is the following figure
3
/ \
9 7
/ \
20 15First, let's assume that we only have arrays traversed in order. What problems will we encounter if we restore a tree.
preorder = [3, 9, 20, 15, 7 ]
First, let's take , 3 , as the root node, and then to , 9, there is a problem. Is 9 , a left subtree or a right subtree?
Therefore, we need to add the array traversed in middle order to determine.
inorder = [ 20, 9, 15, 3, 7 ]
We know that the middle order traversal first traverses the left subtree, then the root node, and finally the right subtree. The first traversal here is 20, which shows that the 9 traversed in advance must be a left subtree, which is proved by the method of counter evidence.
If 9 is a right subtree, according to the preorder traversal preorder = [3, 9, 20, 15, 7], it indicates that the left subtree of root node 3 is empty and the left subtree is empty, then the middle order traversal will traverse root node 3 first, and it is 20 at this time. If it is not true, it indicates that 9 is a left subtree. The next 20 are the same, so the tree you can build now is as follows.
3
/
9
/
20 At the same time, I also notice that the 20 of preorder traversal is equal to the 20 of middle order traversal. What does it mean?
It shows that the next number 15 of middle order traversal is not a left subtree. If it is a left subtree, the first number of middle order traversal will not be 20.
So 15 must be a right subtree. Now there is another question. Is it a right subtree of 20, a right subtree of 9, or a right subtree of 3?
Let's assume several situations and think about it.
If it is the right subtree of 3 and the right subtree of 20 and 9 is empty, the middle order traversal is 20 9 3 15.
If it is the right subtree of 9 and the right subtree of 20 is empty, the middle order traversal is 20 9 15.
If it is the right subtree of 20, then the middle order traversal is 20 15.
The root node that has been traversed before is 3 9 20. Turn it upside down, that is, 20 9 3. Then compare it with the three middle order traversals above, you will find that 15 is the right subtree of the last equal node.
- In the first case, the middle order traversal is 20 9 3 15, which is equal to 20 9 3, so 15 is the right subtree of 3.
- In the second case, the middle order traversal is 20 9 15, and only 20 9 are equal, so 15 is the right subtree of 9.
- In the third case, the middle order traversal is 20 and 15, only 20 are equal, so 20 is the right subtree of 15.
At this time, our middle order traversal array is inorder = [20, 9, 15, 3, 7], 20 matches, 9 matches, and the last match is 9, so 15 is the right subtree of 9.
3
/
9
/ \
20 15To sum up, we use a stack to save the traversed nodes and traverse the array traversed in the previous order as the left subtree of the current root node until the nodes of the current node and the array traversed in the middle order are equal. Then we traverse the array traversed in the middle order in the positive order and the root node traversed in the reverse order (realized by pop of the stack), Find the last equal position and take it as the right subtree of the node.
The above analysis is the overall idea of iteration. Pay attention to some details of the code. Use a stack to save the nodes that have been traversed, and curRoot to save the nodes that are currently being traversed.
public TreeNode buildTree(int[] preorder, int[] inorder) {
if (preorder.length == 0) {
return null;
}
Stack<TreeNode> roots = new Stack<TreeNode>();
int pre = 0;
int in = 0;
//Traverse the first value as the root node first
TreeNode curRoot = new TreeNode(preorder[pre]);
TreeNode root = curRoot;
roots.push(curRoot);
pre++;
//Traversal of pre order arrays
while (pre < preorder.length) {
//The value of the current node is equal to the value of the middle order traversal array. Look for whose right subtree it is
if (curRoot.val == inorder[in]) {
//Each time out of the stack, realize backward traversal
while (!roots.isEmpty() && roots.peek().val == inorder[in]) {
curRoot = roots.peek();
roots.pop();
in++;
}
//Set as current right child
curRoot.right = new TreeNode(preorder[pre]);
//Update curRoot
curRoot = curRoot.right;
roots.push(curRoot);
pre++;
} else {
//Otherwise, it will always be the left subtree
curRoot.left = new TreeNode(preorder[pre]);
curRoot = curRoot.left;
roots.push(curRoot);
pre++;
}
}
return root;
}
This problem is not difficult if you do it with conventional recursion and HashMap. It is not easy to think of using the {stop} variable to omit the idea of HashMap and the iteration of solution 2.